Impact of Fluctuating Energy Prices on the Operation Strategy of a Trigeneration System

Balić, Dražen; Lončar, Dražen

Original scientific paper

Journal of Sustainable Development of Energy, Water and Environment Systems
Volume 3, Issue 3, September 2015, pp 315-332
DOI: https://doi.org/10.13044/j.sdewes.2015.03.0024

Dražen Balić¹ , Dražen Lončar²

¹ Energy Institute Hrvoje Požar, Savska cesta 163, Zagreb, Croatia
² Department of Energy, Power Engineering and Ecology, Faculty of Mechanical Engineering and Naval Architecture, University of Zagreb, Ivana Lučića 5, Zagreb, Croatia

Abstract

Trigeneration systems are potentially more energetically and economically efficient than cogeneration systems due to possibility to extend operation at nominal load. However, these systems also face challenges of future development characterised by reduced heating and cooling demands, as a consequence of implementation energy efficiency measures, and fluctuating electricity prices, as a consequence of increased penetration of intermittent renewable energy sources. The main objective of the paper is to research the operation strategies of trigeneration systems and to derive the optimal ones. The model proposed in this paper consists of two different systems, a conventional system and a trigeneration system. The heating, refrigerating and electric loads are known. The price of gas is constant while electricity prices are fluctuating at hourly basis. The optimization method is based on two criteria – energy and economic, which were applied hierarchically. Therefore, two optimal operation strategies are introduced. A mixed integer non-linear programming model provides energy and cost savings up to 32% and 28% respectively in comparison with conventional system. In addition, optimal capacity of trigeneration system is explored.

Keywords: Trigeneration, Multi-objective optimization, MINLP, Operation strategy.

Views (in 2025): 310 | Downloads (in 2025): 90
Total views: 5632 | Total downloads: 2587

INTRODUCTION

Implementation of trigeneration systems, also known as Combined Heat, Cooling and Power (CHCP) systems, presents a way of efficient use of energy in order to reduce primary energy consumption and to cut expenses [1]. In fact, trigeneration is an upgrade of cogeneration (CHP). Cogeneration is used more often because it is simpler and economically more acceptable (in the sense of the investment cost). The drawback of cogeneration is its lack of use in the part of year when the demands for heating are very small or they do not exist at all. In order to increase operation time i.e. to increase the level of flexibility of the cogeneration system over the year while simultaneously satisfying the refrigeration demand, the cogeneration system should be upgraded with an absorption chiller. In that way this upgraded trigeneration system has a higher degree of freedom and will ensure the reduction of primary fuel consumption due to the fact that less waste heat will be transmitted to the environment. In addition, the trigeneration systems allow better load factors for profit-oriented production [2].

Even more efficient and environmentally more acceptable way of use of natural resources is the concept of polygeneration discussed in [3] where different examples of the polygeneration systems were presented. The importance of distribution of not only cogeneration units, but also the trigeneration systems in the contemporary energy scenario is emphasized by Chicco and Mancarella [4]. In that paper, the influence of distributed generation on the economy is discussed as well. Analyses from the economic point of view are given in [5] where cost allocation in trigeneration systems are analyzed by applying the principle of avoided expenditures. More pragmatic analyses are given by Martins et al. [6]. They have investigated the influence of particular operational variables on the efficiency of the trigeneration system such as compression ratio in the compressor, expansion ratio and efficiency of the turbine, operational pressure in boiler and absorption chiller etc. The most important variables in the process of optimization of trigeneration system are the compression and expansion ratios in compressor and turbine, respectively.

In the year 2010, total energy consumption in the household sector in Croatia was 79 PJ with a share of approx 31% [7]. That represents a huge potential for energy savings, reductions of both operating costs as well as green-house gas emissions by implementing small-scale trigeneration systems, due to the fact that lately significant technological achievements were realized in these systems [8].

Optimal operation strategy of energy systems became imperative due to the desire to achieve high performance in the sense of primary energy and cost reductions. Thus, modeling trigeneration systems can be conducted for various purposes including different criteria. Some authors, such as Lozano et al. [9], Rong and Lahdelma [10], have modeled trigeneration systems by Linear Programming (LP). For determining the type and capacity of optimal CHCP system and its operation strategy, Mixed Integer Linear Programming (MILP) is often used. In [11], MILP techniques are used to determine the optimal configuration of various energy systems such as thermal and electrical storage, renewable energy sources as well as heating and cooling systems. In addition, the impact of variable pricing systems is taken into account. Lozano et al. [12] have used MILP in order to determine optimal operation strategy of the trigeneration systems in tertiary sector buildings which have significant potential for deployment of trigeneration systems, especially in the Mediterranean region. The simulation was conducted on an hour-by-hour basis throughout the year. The importance of in-depth understanding of trigeneration and energy systems is emphasized in [13] where the authors have developed a robust optimization model of trigeneration system coupled with a pressurized thermal storage. The advanced optimization method is given by Fazlollahi et al. [14] where multi-objective optimization model with an evolutionary algorithm based on the MILP is developed. Wang et al. [15] have applied a genetic algorithm to achieve maximum benefits of CHCP system in comparison to conventional system. Trigeneration systems can also be explored by simulation and experiment in order to find the optimal operation strategy. This approach is given by Angisani et al. [16] and Ge et al. [17].

The proposed mathematical model in the present paper is mostly based on the work of Wu et al. [18] and is adapted to the specific conditions of the Croatian energy market. The main objective is to investigate the operation strategies of small-scale trigeneration systems and to derive the optimal ones. The operation strategies of small trigeneration systems have not been investigated broadly mainly because the required equipment was not at a satisfactorily level of development. Earlier, engines, gas turbines and absorption chillers had high efficiencies only at large capacities, but nowadays high efficiencies are available for small capacities as well [8].

The optimization problem is formulated as Mixed Integer Non-Linear Programming (MINLP) and is solved with programming language MATLAB. The basic idea of this paper is to give the optimal operation strategy of small-scale trigeneration system for two different criteria. One is energy efficiency criterion, and the second one is the cost-profit criterion. The trigeneration system will be compared with the conventional system while both of them have to satisfy the same energy loads such as electricity, heat and refrigeration demand.

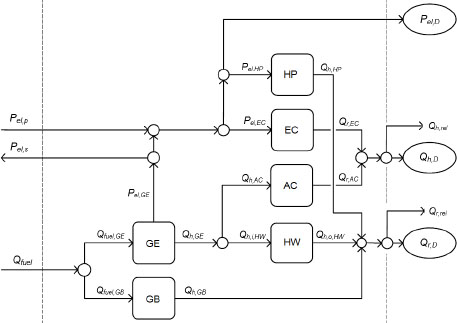
MATHEMATICAL PROBLEM FORMULATION

The proposed CHCP system consists of a Gas Boiler (GB), a Gas Engine (GE), a hot water Heat Exchanger (HW), an Absorption Chiller (AC), an Electric Chiller (EC) and an Electric Heat Pump (HP), as shown in Figure 1. The conventional system is in fact a reduced CHCP system, without gas engine, absorption chiller and hot water heat exchanger (Figure 2). This system will be used as a benchmark. Both systems are connected to public supply network in order to be able to satisfy different energy demands.

Figure 1.

Small-scale CHCP system scheme

Figure 2.

Conventional system scheme

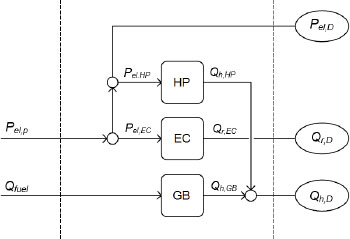
In the case of a small-scale CHCP system, the electric demand as well as electricity consumption of heat pump and electric chiller can be satisfied by electricity produced by the gas engine or by electricity purchased from the public supply network. The refrigeration demand can be served by the electric chiller and by the absorption chiller. The gas boiler, heat pump and heat from the gas engine utilized in the hot water heat exchanger must be able to cover the entire heat demand. The conventional system is simpler and the entire electricity demand is satisfied from the public supply network while the heat and refrigeration demands are satisfied by the heat pump and/or gas boiler and electric chiller, respectively.

To obtain the optimal operating parameters of the mathematical small-scale CHCP model, a few assumptions are introduced:

For any reasonable electricity, heat and refrigerating demands the system must be able to satisfy them. All system components can operate on part load. Of course, the part load cannot be lower than a technical minimum of the component. Apart from the part load variable one more variable is included, namely, a binary on-off variable δ (δ = 1 component operating, δ = 0 component not operating);
In line with the Croatian law for distributed energy systems, it is possible to deliver the surplus of the produced electricity to the public network in which case additional profit is achieved [19]. However, the mathematical model does not allow the possibility to purchase the electricity from the public supply network at a lower price and deliver it back to the public network at a higher price. In other words, the electricity is purchased from the public supply network only when electricity produced by CHCP does not satisfy electric demand of the building. Likewise, in the public supply network electricity can be delivered only under two necessary conditions. First, electricity delivered to the public supply network must be produced by the CHCP and the second, the amount of electricity produced from CHCP must be greater than the electric demand of the building, i.e. it possible to deliver into the public supply network only the difference of electricity produced by CHCP and the electricity demand of the building. Otherwise, it is not possible to deliver electricity to the public supply network and gain additional profit;
Independently of the optimization criterion i.e., optimization type small-scale CHCP system is always compared with the conventional system operating under the optimal parameters. It means, if the energy optimization is conducted, the small-scale CHCP system will be compared with the conventional system under such parameters which will assure the maximum energy saving and the cost saving will be less important. For the cost optimization it would be reversed;
The performance of the devices is divided into two groups: the constant ones and load dependent variables. Performance of the heat pump, electric chiller, gas boiler and hot water heat exchanger is constant while the load dependent performance is modelled with quadratic approximation and will be explained later;
The fuel price for the gas engine and gas boiler is known and is constant, while the price of electricity purchased and sold fluctuates on an hourly basis;
In the model proposed by this paper, all investment costs as well as economic analyses were neglected.

Objective function formulation

This model gives two types of the optimization. In both optimization types two criteria are involved. The first one is energy saving and the second one is cost saving. Different criteria will lead to different operation strategies. In order to find the optimal operation strategies, i.e. to find the maximum savings (energy and/or cost) two factors are defined. The Energy Factor (EF) and the Cost Factor (CF), referring to how much the CHCP system is better than the conventional system in the sense of the primary energy consumption and cost, respectively. Each of them should be less than one (EF, CF ∈ ⟨−∞, 1] ⊂ ℝ). The energy factor is defined as:

EF = \frac{Q_{tot}^{CONV} - Q_{tot}^{CHCP}}{Q_{tot}^{CONV}}

(1)

where $Q_{tot}^{CONV}$ and $Q_{tot}^{CHCP}$ symbolize the total primary energy consumption of the conventional system and the small-scale CHCP system, respectively. The total primary energy is given as:

Q_{tot}^{i} = Q_{fuel}^{i} + P_{el, p}^{i} PEF

(2)

where superscript i denotes the Conventional system (CONV) or the small-scale CHCP (CHCP). Q_fuel is total gas consumption for given system while P_el,p is total electricity purchased from public supply network. PEF is a Primary Energy Factor, and its value for Croatian market is given in Table 1.

Table 1.

Characteristics of components

Characteristic	Value
P_el,GE,nom	50 kW
Q_h,GB,nom	20 kW
COP_HP	2.6
COP_EC	3.2
ηHw	0.95
ηGB	0.9
PEF	3

Similarly, the cost factor is defined as:

CF = \frac{{COST}^{CONV} - {COST}^{CHCP}}{{COST}^{CONV}}

(3)

where COST^CONV and COST^CHCP symbolize the total operation cost of the conventional and the small-scale CHCP system, respectively. The total cost can be calculated as:

{COST}^{CONV} = p_{gas} Q_{fuel}^{CONV} + p_{el, p} P_{el, p}^{CONV}

(4a)

{COST}^{CHCP} = p_{gas} Q_{fuel}^{CHCP} + δ_{el} p_{el, p} P_{el, p}^{CHCP} - (1 - δ_{el}) p_{el, s} P_{el, s}^{CHCP}

(4b)

where p_gas, p_el,p and p_el,s are the gas price, price for purchased electricity from the public supply network and price for sold electricity to the public network, respectively. δ_el is a binary on-off variable (δ_el ∈ {0,1} ) and it disables the possibility of simultaneously selling the produced electricity surplus and purchasing electricity from the public supply network.

The objective of the optimization is to find for every demand condition the maximal energy factor:

{EF}_{opt} = max {\frac{Q_{tot}^{CONV} - Q_{tot}^{CHCP}}{Q_{tot}^{CONV}}}

(5)

for energy based optimization and the maximal cost factor for cost based optimization type:

{CF}_{opt} = max {\frac{{COST}^{CONV} - {COST}^{CHCP}}{{COST}^{CONV}}}

(6)

Equations and restrictions formulation

This section gives an overview of a set of limits, constraints and balance equations for each system component and subsystem. Capacity limits are defined as:

Gas engine; $P_{el, GE} \leq P_{el, GE, nom}$ (7)
Absorption chiller; $Q_{r, AC} \leq Q_{r, AC, nom}$ (8)
Gas boiler; $Q_{h, GB} \leq Q_{h, GB, nom}$ (9)

where subscript nom in eq. (7–9) denotes to a nominal power output of the given system component. From eq. (7–9) it can be concluded that in the proposed mathematical model every heat and refrigeration demand can be satisfied due to the fact that the heat pump and electric chiller have an infinite capacity. In the real physical model it is impossible, but for this analysis it is acceptable if the demands are in a reasonable range.

The gas engine unit can be described with following equations:

P_{el, GE} = δ_{GE} Q_{fuel, GE} η_{el, GE}

(10)

Q_{h, GE} = δ_{GE} Q_{fuel, GE} η_{h, GE}

(11)

{PLF}_{GE} = \frac{P_{el, GE}}{P_{el, GE, nom}}

(12)

η_{el, GE} = a_{1} {PLF}_{GE}^{2} + a_{2} {PLF}_{GE} + a_{3}

(13)

η_{h, GE} = b_{1} {PLF}_{GE}^{2} + b_{2} {PLF}_{GE} + b_{3}

(14)

where δ_GE is a binary on-off variable (δ_GE ∈{0,1} ) while η_el_,GE and η_h_,GE denote the electric and heat efficiencies of the gas engine respectively and PLF_GE is the part load factor of the gas engine. a_i and bi where i = 1, 2, 3 are dimensionless factors given in Table 1.

Similarly, the absorption chiller can be described as:

Q_{r, AC} = δ_{AC} Q_{h, AC} {COP}_{AC}

(15)

{PLF}_{AC} = \frac{Q_{r, AC}}{Q_{r, AC, nom}}

(16)

{COP}_{AC} = c_{1} {PLR}_{AC}^{2} + c_{2} {PLR}_{AC} + c_{3}

(17)

where δAC is a binary on-off variable (δAC ∈{0,1} ) while COP_ac is the coefficient of performance for the absorption chiller while PLF_AC is the part load factor of the absorption chiller. ci where i = 1, 2, 3 are dimensionless factors given in Table 1.

The gas boiler is described with following equations:

Q_{h, GB} = δ_{GB} Q_{fuel, GB} η_{GB}

(18)

{PLF}_{GB} = \frac{P_{GB}}{P_{GB, nom}}

(19)

where δ_GB is a binary on-off variable (δ_GB∈ {0,1} ) while η_GB denotes the efficiency of the gas boiler while PLF_GB is the part load factor of the gas boiler.

The hot water heat exchanger:

Q_{h, o, HW} = δ_{HW} Q_{h, i, HW} η_{HW}

(20)

where δ_HW is a binary on-off variable (δ_HW ∈{ 0,1} ) while η_HW is the efficiency of the hot water heat exchanger. Q_h,o,HW and Q_h,i,HW denote the heat input to and heat output from the hot water heat exchanger, respectively.

The heat pump and electric chiller:

Q_{h, HP} = δ_{HP} P_{el, HP} COP P_{HP}

(21)

Q_{h, EC} = δ_{HP} P_{el, EC} {COP}_{EC}

(22)

where δ_Ηρ and δ_ΕC are binary on-off variables (δ_Ηρ , δ_ΕC ∈{0,1} ) for the heat pump and electric chiller, respectively, while COP_hp and COP_ec are the coefficients of performance of the heat pump and electric chiller, respectively.

In order to completely define the mathematical model, five additional energy balance equations are needed.

Electric energy balance:

δ_{el} P_{el, p} + P_{el, GE} = P_{el, D} + (1 - δ_{el}) P_{el, s}

(23)

Heat energy balance:

Q_{h, GB} + Q_{h, o, HW} + Q_{h, HP} = Q_{h, D} + Q_{h, rel}

(24)

Q_{h, GE} = Q_{h, i, HW} + Q_{h, AC}

(25)

where Q_h,D and Q_h,rel denote the heat demand and extra cogeneration heat released to the environment, respectively. Q_h,rel can occur in some situations and it can be wasted without additional cost.

Refrigeration energy balance:

Q_{r, AC} + Q_{r, EC} = Q_{r, D} + Q_{r, rel}

(26)

where Q_r,D and Q_r,rel denote the refrigeration demand and absorption chiller extra refrigeration energy released to the environment, respectively. Q_r,rel is possible to occur in some situation and it also can be wasted without additional cost.

Fuel balance:

Q_{f} = Q_{f, GE} + Q_{f, GB}

(27)

All equations described above are applicable for both systems, the conventional one and the small-scale CHCP system. Of course some equations do not have relevance to the conventional system.

Optimization procedure

The optimization method is based on the two criteria – energy and cost. Both these criteria were applied on the conventional system and on the small-scale CHCP system. Optimization is based on the comparison between the conventional and small-scale CHCP system with respect to the total primary energy and on the total operation cost. The criteria were applied hierarchically. After the optimization was carried out by one of the criteria, the set of optimal solutions was found. The second criterion was then applied on the optimal solution set given by first criterion. Solution given by the second criterion is the optimal one. Therefore, two optimal operation strategies could be found, depending on which criterion is more relevant – energy savings or cost savings. The optimization flowchart is shown in Figure 3.

Figure 3.

Optimization method flowchart

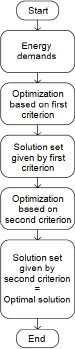
As mentioned above, the model is aggregated by two systems. The conventional system consists of three components and due to the assumption that all demands are known, this system has only one degree of freedom. It means that if the load of one component is determined, the loads of two other components are determined as well. Hence, by varying the load of the gas boiler it is possible to find out the optimal solution (minimal primary energy consumption or operation cost) for each observed moment i.e. for any demand combination. With the small-scale CHCP system the situation is slightly different. The system consists of six components and this system has three degrees of freedom. The strategy of the optimization method is to vary the load of the gas engine, gas boiler, and absorption chiller. In that way, the loads of all the others components are determined for each observed moment i.e. for any demand combination too. For the each observed moment, all the possible operation strategies of the CHCP system were carried out and energy or cost factors (depending on hierarchical policy) were calculated using the optimal solution of the conventional system for that observed moment. Those factors were compared and the maximal ones were remembered. They constitute the optimal solution set for the observed moment. The next step was to apply second criterion and from the optimal solution set, to derive the optimal solution.

It can be concluded that the optimization problem is three dimensional and it was solved by means of programme language MATLAB.

Input data

In order to carry out the optimization it is necessary to define some general features of the mathematical model. Characteristics of some components are set to fixed values and are given in Table 1.

The three components do not have constant parameters (eq. 13, 14, 17). Their dimensionless factors are given in Table 2.

Table 2.

Dimensionless factors [20], [21]

Characteristic	Value	Characteristic	Value	Characteristic	Value
a₁	−0.086	b₁	0.0375	c₁	−0.2361
a₂	0.1914	b₂	−0.0525	c₂	1.376
a₃	0.2618	b₃	0.498	c₃	−0.7656

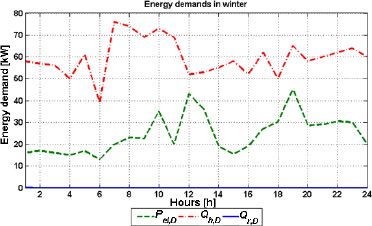
This model is applied to a characteristic building in the city of Zagreb (Croatia). The observed building is of energy class D with an annual consumption of approximately 125 kWh/m². The total useful area of the building is 1,800 m² with approximately 80 tenants. The specific heat and refrigerating demands for the observed building are modeled on the basis of [22] for two characteristic days, one in the winter season and the other in summer

season. The demands are shown in Figures 4 and 5 for the winter and summer day, respectively.

Figure 4.

Energy demands-winter day

Figure 5.

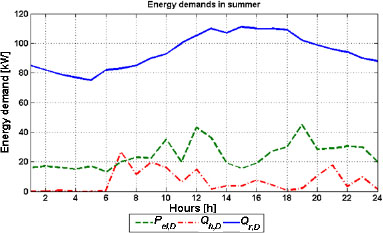
Energy demands-summer day

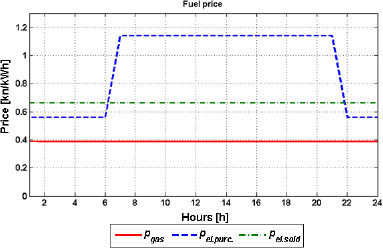
Price scenarios are also known and shown in Figure 6.

Figure 6.

Price scenario

RESULTS

As can be seen in Figure 4 during the winter season, refrigeration demand is equal to zero. Due to that fact, in winter days the small-scale CHCP system operates like the regular cogeneration system (CHP) and supplies only the electricity and heat. After the winter day results are presented and discussed, similar analyses will be given for the day in summer season. At the end of this section, it will be investigated which nominal power of the gas engine generates the highest energy and cost savings on the base of one characteristic day.

Winter day analyses

As it was explained earlier, two types of the optimization were carried out. First, the results for the energy cost optimization will be presented.

Energy cost optimization - winter day.

In Figures 7 and 8 are shown the optimization results for winter where the energy criterion was the dominant one. It can be seen that the energy factor follows the gas engine heat curve. It confirms that the energy factor is higher when the small-scale CHCP system is under higher load. These two figures must be observed together with Figure 4. It can be seen that when the heat demand decreases, the load ratio of the gas engine also decreases. This is in accord with eq. (13) and (14) due to the fact that the efficiency of the gas engine decreases as the load ratio decreases. The energy factor has decreased in the 15^th hour due to the fact that the electric demand has rapidly fallen while simultaneously the heat demand has increased. This combination leads to the fact that operation strategy of the CHCP starts getting closer to the conventional system. The cost factor is less than zero in the periods of the day when the electricity price is low (Figure 6). It means that in those periods the CHCP system is more expensive than the conventional system.

Figure 7.

Optimal operation strategy-winter day energy-cost optimization

Figure 8.

Savings factors-winter day energy-cost optimization

On the base of the entire winter day, total energy saving goes up to 31.9% in comparison with the conventional system while total cost saving reaches 22.3%.

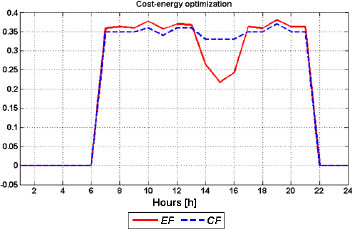
Cost energy optimization - winter day.

In the case of cost based optimization (Figure 9), the heat pump takes most of the heat demand, especially during the night hours when the electricity price is low. The gas boiler doesn’t participate in the energy balance. The heat pump operation regime is mostly determined by the electricity demand due to the fact that the CHCP has the intention of satisfying electricity demand. During the low electricity price period, cost and energy factor (Figure 10) are equal to zero, which implies that the CHCP system operates as efficiently as the conventional system. The total cost and total energy savings in the case of cost-energy optimization are 28.4% and 23.4%, respectively.

Figure 9.

Optimal operation strategy-winter day cost-energy optimization

Figure 10.

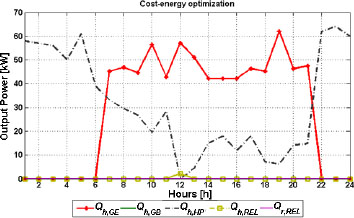
Savings factors-winter day cost-energy optimization

Summer day analyses

During the characteristic summer day in the area of the city of Zagreb the refrigeration demand is significant (Figure 5). In this case the small-scale CHCP system operates fully as the trigeneration system provides electricity, heat and refrigeration. The energy cost optimal strategy is introduced first.

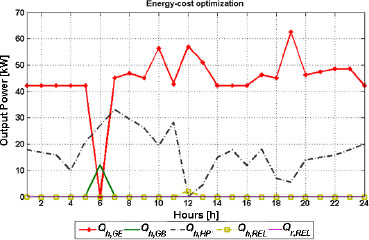
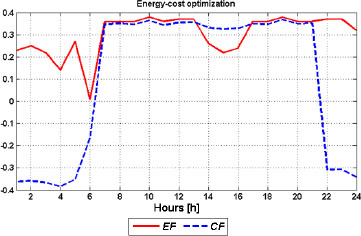
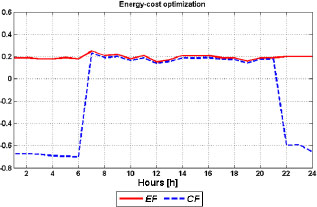
Energy cost optimization - summer day.

In Figures 11 and 12 are shown the optimal operation strategy for the energy cost optimization type and savings factors, respectively. The most exposed curve in Figure 11 is refrigeration by the electric chiller. This high rate of the electric chiller is a consequence of high refrigeration demand during the summer day (Figure 5) and fact that the absorption chiller cannot satisfy it since the gas engine power is limited. The energy factor is all the time around 20% while the cost factor sharply increases when the electricity price becomes higher and sharply decreases when the electricity again becomes cheaper. The same situation was in the winter day case where during the night hours the small-scale CHCP system operates in more expensive way than the conventional system. The total energy and cost savings are 19.1% and 2.9%, respectively.

Figure 11.

Optimal operation strategy-summer day energy-cost optimization

Figure 12.

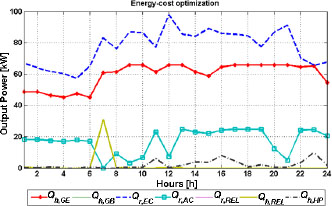
Savings factors-summer day energy-cost optimization

Cost energy optimization - summer day.

As is shown in Figure 13 the optimal operation strategy for the summer day under the cost energy optimization is similar to the energy cost optimization (Figure 11). The difference only exists during the night hours when the electricity price is low. In those periods all demands are covered by the electric chiller or the heat pump i.e. by the electricity as a base fuel.

Figure 13.

Optimal operation strategy-summer day cost-energy optimization

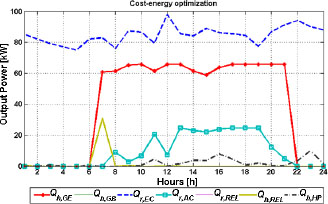
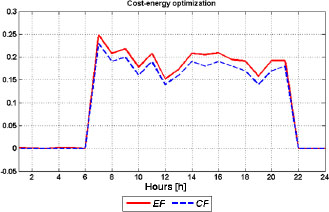
Savings factors in this case, as shown in Figure 14, are not expected since the energy factor is greater than the cost factor. However, those factors should be compared with the savings factors from section Energy cost optimization – summer day since the total cost and energy factor for the cost energy optimization are 14.5% and 13.4%, respectively, while in the energy cost optimization they are 2.9% and 19.1% respectively.

Figure 14.

Savings factors-summer day cost-energy optimization

Optimal gas engine power

Apart from finding the optimal operation strategy for the given technical system another important parameter is the nominal power of the system which satisfies all types of energy demands. Since the gas engine nominal power defines the power i.e. capacity of the small-scale CHCP system this chapter more carefully analyses the influence of the gas engine nominal power on the energy and cost factors. Analysis has been conducted for a characteristic winter and summer day and calculated factors represent savings for the entire day.

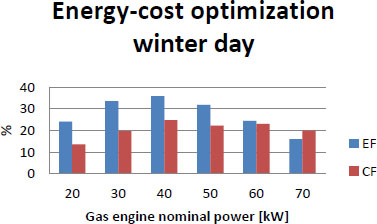
In Figures 15 and 16, the influence of the gas engine nominal power to the savings outcome during the winter day is given. It can be seen that the highest savings are reached when the power is set to the value of 40 kW, regardless of which optimization type is conducted. What is perhaps interesting is the fact that the CF is greater than the EF in Figure 15 even though it is energy cost optimization and it would be expected that the EF is always greater than the CF. It is acceptable if the CF value from Figure 15 is compared with the CF value from Figure 16 for the given nominal power. The value from energy cost optimization must be smaller than the value from the cost energy optimization and that is the case.

Figure 15.

Savings factors for different gas engine nominal power – Energy cost optimization-winter day

Figure 16.

Savings factors for different gas engine nominal power – Cost energy optimization-winter day

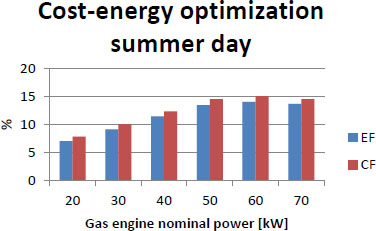
From Figures 17 and 18, it is obvious that optimal power for gas engine during summer season would be 60 kW. Due to the fact that for winter season optimal power would be 40 kW in all analysed cases 50 kW was the adopted value for the gas engine nominal power. In addition, it is possible to achieve much higher savings during the winter season regardless of the optimization criterion.

Figure 17.

Savings factors for different gas engine nominal power - Energy cost optimization-summer day

Figure 18.

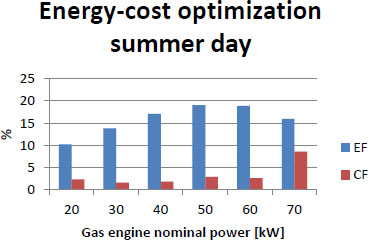
Savings factors for different gas engine nominal power – Cost energy optimization-summer day

CONCLUSIONS

In this paper a multi-objective optimization method for a small-scale trigeneration system is proposed. Trigeneration as a concept has very small, almost negligible, share in distributed generation in Croatia. Therefore, this paper and the findings in it can contribute to foster the deployment of small-scale trigeneration systems not only in residential houses but also in multi apartment buildings. Moreover, contemporary energy systems are faced with inevitable transition mainly due to increased share of RES. In that sense, the small-scale system for distributed generation could have a significant role in that transition.

The multi-objective optimization method was based on two criteria - energy savings criterion and cost savings criterion. The optimization procedure has shown that possible energy savings can yield the level of around 35% compared with conventional system in the case when energy savings are the dominant criterion. Somewhat lower savings are achieved (around 32%) when the cost saving is the dominant criterion. The second criterion is more relevant in the sense of the implementation of such energy systems. Moreover, the performance of the trigeneration system compared to the conventional system is significantly better during the winter period when in fact trigeneration system operates as a cogeneration. This is a direct consequence of an additional energy conversion (in absorption chiller), i.e. additional energy loss. Nevertheless, the benefits of the trigeneration system are more than obvious.

Results obtained in this research can be used not only for promotion of distributed generation, particularly the small-scale trigeneration systems suitable for domestic use, but also for creation, adoption, modification, and refining energy policies and regulations on national as well as on regional level. Particular attention should be paid to the small-scale trigeneration systems and their potential impact not only on the environment but also on the national and local economy. This should be taken into consideration primarily by policy makers. However, end users should also be involved.

Furthermore, the impact of fluctuating electricity prices on the optimal operation strategy of the small-scale trigeneration system is investigated in the paper. The price of natural gas was held constant even though it is possible to expect it to fluctuate on an hourly basis. The analyses of the fluctuating natural gas price as well as the impact of ratio of electricity to natural gas price on the optimal operation strategy should be one of the following steps in future research. In addition, the influence of heat storage tank coupled with the small-scale trigeneration system should also be done, together with determination of optimal operation strategy of such an extended system.

NOMENCLATURE

CF	Cost factor	[-]
COST	Total operation cost	[kn]
EF	Energy Factor	[-]
P	Electric power	[kW]
PEF	Primary energy factor	[-]
PLF	Part load ratio	[-]
Q	Heat	[kW]
δ	Binary	[on-off variable]

Superscripts

CHCP	Combined Heat, Cooling and Power system
CONV	Conventional system
i	The system type index (CONV or CHCP)

Subscripts

el	electric
h	heat
i	input
nom	nominal
o	output
p	purchased
r	refrigerating
rel	released
s	sold
tot	total

REFERENCES

Hernandez-Santoyo J., Sanchez-Cifuentes A., Trigeneration: An Alternative for Energy Savings, Applied Energy, Vol. Vol. 76 , :219-2272003, https://doi.org/10.1016/S0306-2619(03)00061-8
Schicktanz M., Wapler J., Henning H., Primary Energy and Economic Analysis of Combined Heating, Cooling and Power Systems Energy, Vol. Vol. 36 , :575-5852011, https://doi.org/10.1016/j.energy.2010.10.002
Serra L., Lozano M., Ramos J., Ensinas A., Nebra S., , Polygeneration and Efficient use of Natural ResourcesEnergy, Vol. Vol, 34 , :575-5862009, https://doi.org/10.1016/j.energy.2008.08.013
Chicco G., Mancarella P., Distributed Multi-generation: A Comprehensive View, Renewable & Sustainable Energy Reviews, Vol. Vol. 13 , :535-5512009, https://doi.org/10.1016/j.rser.2007.11.014
Lozano M., Cravalho M., Serra L., Allocation of Economic Costs in Trigeneration Systems at Variable Load conditions, Energy and Buildings, Vol. Vol. 43 , :2869-28812011, https://doi.org/10.1016/j.enbuild.2011.07.002
Martins L., Fábrega F., d’ Angelo J., Thermodynamic Performance Investigation of a Trigeneration Cycle Considering the Influence of Operational Variables, Procedia Engineering, Vol. Vol. 42 , :1879-18882012, https://doi.org/10.1016/j.proeng.2012.07.584
, Croatian Ministry of Economy, Labour and Entrepreneurship, Energy in Croatia 2010, Annual energy report, 2011
, , Polysmart, Technology and Literature Review.,
Lozano M., Cravalho M., Serra L., Operational Strategy and Marginal Costs in Simple Trigeneration Systems, Energy, Vol. Vol. 34 , :2001-20082009, https://doi.org/10.1016/j.energy.2009.08.015
Rong A., Lahdelma R., An Efficient Linear Programming Model and Optimization Algorithm for Trigeneration, Applied Energy, Vol. Vol. 82 , :40-632005, https://doi.org/10.1016/j.apenergy.2004.07.013
Ashouri A., Fux S., Benz M., Guzzella L., Optimal Design and Operation of Building Services using Mixed-integer Linear Programming Techniques, Energy, Vol. Vol. 59 , :365-3762013, https://doi.org/10.1016/j.energy.2013.06.053
Lozano M., Ramos J., Cravalho M., Serra L., Structure Optimization of Energy Supply Systems in Tertiary Sector Buildings, Energy and Buildings, Vol. Vol. 41 , :1063-10752009, https://doi.org/10.1016/j.enbuild.2009.05.008
Piacentino A., Cardona F., EABOT - Energetic Analysis as a Basis for Robust Optimization of Trigeneration Systems by Linear Programming, Energy Conversion and Management, Vol. Vol. 49 , :3006-30162008, https://doi.org/10.1016/j.enconman.2008.06.015
Fazlollahi S., Mandel P., Becker G., Maréchal F., Methods for Multi-objective Investment and Operating Optimization of Complex Energy Systems, Energy, Vol. Vol. 45 , :12-222012, https://doi.org/10.1016/j.energy.2012.02.046
Wang J., Jing Y., Zhang C., Optimization of Capacity and Operation for CCHP System by Genetic Algorithm, Applied Energy, Vol. Vol. 87 , :1325-13352010, https://doi.org/10.1016/j.apenergy.2009.08.005
Angrisani G., Rosato A., Roselli C., Sasso M., Sibilio S., Experimental Results of a Micro-trigeneration Installation, Applied Thermal Engineering, Vol. Vol. 38 , :78-902012, https://doi.org/10.1016/j.applthermaleng.2012.01.018
Ge Y., Tassou S., Chaer I., Suguartha N., Performance Evaluation of a Tri-generation System with Simulation and Experiment, Applied Energy, Vol. Vol. 86 , :2317-23262009, https://doi.org/10.1016/j.apenergy.2009.03.018
Wu J., Wang J., Li S., Multi-objective Optimal Operation Strategy Study of Micro-CCHP System, Energy, Vol. Vol. 48 , :472-832012, https://doi.org/10.1016/j.energy.2012.10.013
, Government of the Republic Croatia, Tariff System for the Production of Electricity from Renewable Energy Sources and cogeneration OG 63/12, 2012
Li S., Wu J., Theoretical Research of a Silica Gelewater Adsorption Chiller in a Micro Combined Cooling, Heating and Power (CCHP) system, Applied Energy, Vol. Vol. 86 , :958-672009, https://doi.org/10.1016/j.apenergy.2008.09.016
Energy and Environmental Analysis Inc. an ICF Company, , 2008
, Energy Demands in Building Sector in the City of Zagreb, from personal correspondence with Mrs. D. Maljković, Energy Institute Hrvoje Požar.,