The Heat Pump (HP) technology is used to produce heating water for household use. If the grid supply is decarbonised, using HP allows to significantly reduce the carbon dioxide emissions, compared to traditional technologies such as boiler [1]. Coefficient of Performance (COP) is a key point in product marketing and energy labelling. There are different test standards for HP Water Heaters (HPWHs) in use in different regions of the world. As a result, manufacturers have to undertake a different set of tests for each economy where they sell their products. This adds to product cost and slows the development of the global market. A way to avoid this is to develop a HPWH COP model based on a limited number of tests. Ideally, the model allows local regulators to determine the COP of products under local test conditions, without conducting additional physical tests.

The principles of HPWH operation are well understood and some existing models allow HPWH performance to be accurately simulated. Modelling a heat pump is generally divided into two categories: polynomial fits and semi-empirical. In the first category, the correlations are fitted to experimental data as the models presented in [2]-[4]. The semi empirical approach, for instance the model used in the papers [5]-[7], is based on thermodynamic evolutions of the working fluid through the components of the heat pump. The model requires data to calibrate its parameters. Some models can be used only for steady state working conditions, such as the model presented in [8], while others allow to study dynamic conditions including the start-up phase and defrosting phase [9], [10]. The common point of these cited works is that the models are used to predict the COP at an ambient condition which remains constant during the simulation. It is also possible to estimate the average COP over a season during which the ambient condition changes continuously in time [11], [12].

Reviews are presented in [13]-[15] on simulation techniques for heat pump systems, not only the well-established techniques but also the developing techniques such as the Artificial Neural Network (ANN) technique [16] and the fuzzy theory [17]. It should be noted that all these models are relatively sophisticated, require significant input data [13] and thus are difficult to use in a regulatory environment.

In this context, it is interesting to study the possibility of developing a simplified performance model built from a number of experimental test results and then to examine the predictive capability of the model developed.

Determination of the coefficient of performance. Under steady-state working conditions, the instantaneous coefficient of performance is defined as the ratio of the heating power Q˙ produced by the HPWH and the electric power W˙:

In general, COP_ins depends mainly on the operating conditions, including the ambient temperature and the water temperature. During a standard performance test, the ambient temperature is set to be constant but the tank temperature varies. In this situation, the coefficient of performance is defined by integration over the test duration:

where the subscripts int, i and f refer to integrated, initial moment and final moment respectively.

If the heat-up phase without a draw off cycle is considered in isolation, the heating power can be calculated from the tank temperature variation as follows:

where:

• m is the water mass contained in the tank;

• c_p is the specific heat capacity of the water;

• T_t is the tank water temperature (T˙_t is then derivative of temperature as function of time).

In addition, the principal variable can be changed from time to the tank water temperature as follows:

because m and c_p are practically constant. (Eq. 4) allows the COP_int to be calculated if the variation of COP_ins as a function of T_t is known. The next section presents some correlation-based models of COP_ins as a function of T_t, drawn from the scientific literature.

Existing correlation models. According to [18], for an air cooled HPWH, the instantaneous performance can be expressed by:

where a₁, a₂, a₃ are constants; and the subscripts d, w and dew refer to dry bulb, wet bulb and dew point of the surrounding air temperature, respectively. This correlation model was validated using experimental data from two HPWHs: one with a wrap-around condenser coil and the other with an external condenser. The tests were carried out under different ambient conditions without a draw-off cycle. Compared to the measured values, the correlation model gave an average error of 4% with a maximum error of about 15%.

During the development of the Australian/New Zealand Standard (AS/NZS) [19], a number of alternative correlation functions, including the model presented above, were investigated from which the following model was selected:

In another analysis of an air-cooled HPWH, known as the EnergyPlus simulation [20], the following correlation is proposed:

where the c coefficients are constants, and T_a is either the dry bulb temperature or the wet bulb temperature of the ambient air.

It should be noted that all these correlations were developed to predict the HPWH performance for the whole range of operating conditions. For this reason, they require much experimental data to determine correctly the coefficients. In addition, they were only tested in the heat-up phase, their predictive capability is then not known during a whole cycle including both heat-up and draw-off phases.

Objective of the current study. The main objective of the current study is to propose a methodology of simulation which can be used for both a heat-up phase considered in isolation and a whole working cycle including draw-off phases. The model will be based on polynomial functions where the variables are water and air temperatures and the regression coefficients are derived from a very limited experimental data. In particular, we will use the AS/NZS standard test data because, among the existing standards, the AS/NZS standard requires the greatest number of different test conditions during the heat-up phase. The model estimates the COP of the same HPWH under other test standards (i.e. US, Japanese, European and Korean standards), and the simulation results will be compared to measured values.

Specifically, the accuracy of the AS/NZS model of COP, which is the last developed instantaneous COP model, will be tested against a HPWH data. This model contains 4 variables of temperature. It is worth noting that the air temperatures (T_d, T_w and T_dew) are generally correlated in the test standards.

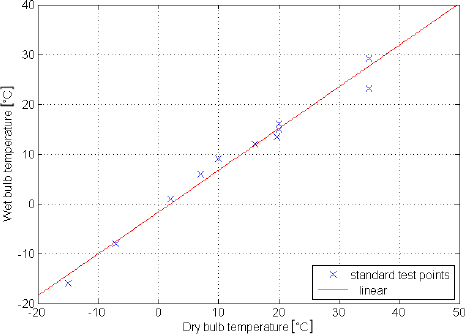
Figure 1 shows dry bulb and wet bulb temperatures collected from different standards, the coefficient of determination R² is equal to 0.98. Therefore including all 3 air temperatures in the correlation model presents a degree of redundancy and is therefore probably inappropriate. For this reason, we propose to test a three-variable model based on T_d and T_w and a two-variable based only on T_w. In summary, the current study investigates the following correlation models:

Figure 1.

Coincident wet bulb and dry bulb temperatures of the different test standards, including Australian/New Zealand, US, Japanese, European and Korean standards [19], [21]-[24]

The coefficients can be determined by regression using physical test data. While the air temperatures are obtained from measurements made of the ambient air, the most appropriate data used to define the water temperature T_t varies with the HP system technology. In general, T_t should be the average water temperature in the condenser. In the case of separate HPWHs that have a circulation pump between the tank and the HP, T_t is a function of the temperature at the inlet and outlet of the condenser. For integral condenser HPWHs, the definition of the tank water temperature should be based on the average water temperature over the depth of the condenser coil positioned in the tank or wrapped around the tank. Due to the difficulty of applying this definition in real life, an alternative way is to consider T_t as the tank water temperature averaged over the whole depth of the tank. In principle this could introduce significant error if the temperature at the condenser inlet significantly differs from the water tank temperature (for separate tank-HP systems) or if the tank is stratified (for integral condenser HPs).

This section illustrates how a HPWH COP model can be developed and investigates the precision of the models derived.

Figure 2 summarises the main modelling steps, which are subsequently explained in the text.

Figure 2.

Methodology for modelling HPWH energy performanc

Data pre-treatment. First, the raw data needs to be pre-treated. When the data is recorded at a short interval of time, a high level of statistical noise may be observed. Given this, it is better to average the measured data over an appropriate period of time during which the water temperature variation is significant, especially when compared to the measurement uncertainty. In this paper, two levels of temperature variation are studied: 1 K and 5 K.

Correlation model determination. The least squares method is used to determine the parameters of the three correlation models presented in (eq. 8-10).

Outliers. An outlier is defined as an observation that is separated in a particular way from the rest of the data set. In a heating-up phase test, there are generally outliers at the beginning and at the end of the test. The outliers should be removed from the data because they can significantly affect the parameters derived for the correlation model. One effective way to find outliers is via residual analysis. In this analysis, a criterion of a “studentised residual” of greater than 3 is used to define an outlier.

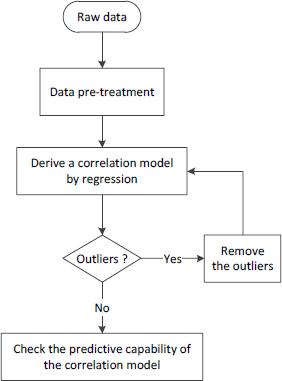
Once the outliers have been excluded, a regression model can then be refitted to the data. It is for this reason that an iterative loop is required to repeat the regression until there are no outliers left.

Validation of the correlation model. In order to test the validity of the correlation model experimental data of another test is used to check the predictive capability of the correlation model obtained. Specifically, the estimated COP_ins derived from the correlation model is compared to the measured values. Finally, the COP_int over the entire test is determined using (eq. 4). The predictive capability of the model is quantified via the error of the model, which is defined as:

Description. The machine tested in this study is an air source heat pump water heater. It is monobloc type and uses the basic refrigeration cycle, as shown in Figure 3. The water heater is connected, via hydraulic pipes, to a storage tank. The tank volume is not directly measured, but taken from the technical documentation of the tank. Sensors are installed according to the AS/NZS standard [19]. In particular, water temperatures and flowrate are measured, with sensor uncertainties of 1 K and 2%, respectively. The electric consumption of the HPWH is also measured (sensor uncertainty of 2%), allowing to calculate the COP of the system.

Figure 3.

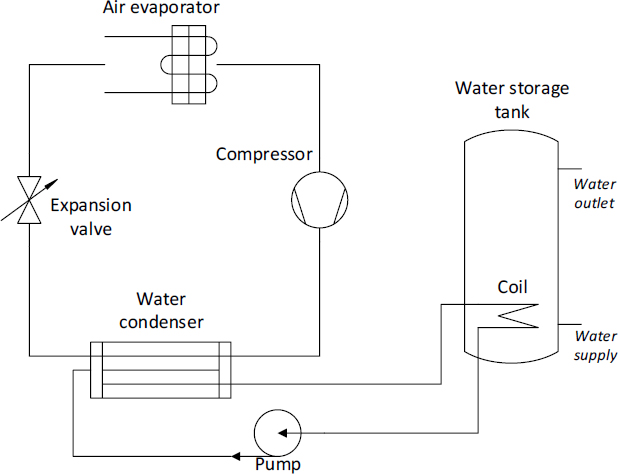
Scheme of the tested HPWH

Among existing international performance test standards, the AS/NZS standard [19] is the standard that requires the greatest number of different test conditions during the heat-up phase (Table 1). So, in principle a correlation model fitted to the AS/NZS test data could help in predicting heat-up phase performance of other international test standards. For this reason, regression models are derived from a set of four AS/NZS standard tests applied to a HPWH, according to the methodology proposed in Figure 2.

The predictive capability of the models obtained is then verified using test data for the same HPWH measured under the following standards: USA [21], Europe [22] and Japan [23]. The assessment only considers and applies to the heat-up phase without drawoff. The predictive capability of the correlation models are also compared to three sets of test data measured under the Korean Standard [24]. These tests are performed under steady state conditions where the water is continuously drawn off with a constant water flow rate. Table 2 summarises the operational conditions applied in the different test standards.

Predictive capability of the model developed. As an example for the regression step, Figure 4 shows the regression model of three variables developed from the data of AS/NZS tests. The model gives satisfactory regression R² coefficients of 90%. One can observe that the outliers are at the beginning and at the end of each test.

Figure 4.

COP_ins correlation models derived from the four AS/NZS standard tests

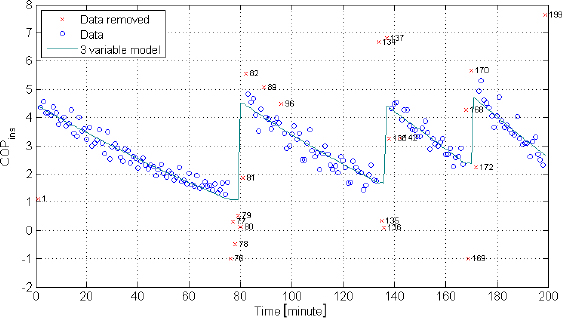
Figure 5 shows the correlation models from US standard test, compared to the measured data, where the correlation models are built from 1 Kelvin interval data. The COP_ins values predicted by the models are relatively close to the measured values.

Figure 5.

COP_ins predictive from the correlation models compared to COP_ins measured

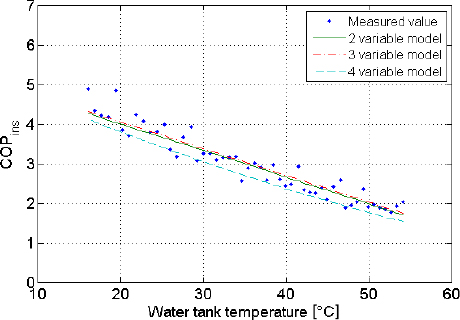
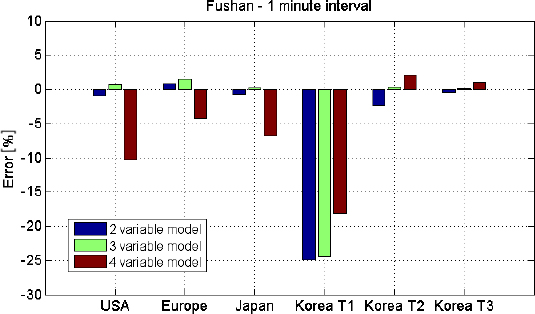
Figure 6 and Figure 7 exhibit graphically the error ε in the 1-Kelvin interval data and 5-Kelvin interval data models. In both cases, the models obtained have reasonable precision for almost all the test standards, except for the Korean test n°1. The main difference between this test and the others relates to the very low inlet water temperature when compared to the water tank temperature. As discussed in part “HPWH simulationfundamentals”, this is because the correlation models are likely to be inaccurate when the tank water temperature differs greatly from the condenser water temperature.

Figure 6.

Error in COP_int predicted by the correlation models derived from 1-Kelvin interval data compared to experimental measurements

Figure 7.

Error in COP_int predicted by the correlation models derived from 5- Kelvin interval data compared to experimental measurements

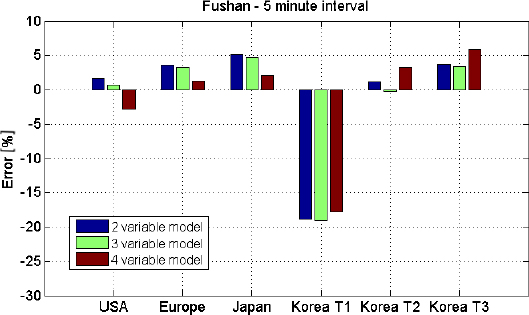
Except for the Korean test n°1, the two-variable and three-variable models have a precision better than 5%. In almost all cases, the four-variable model produces relatively large errors. This may lead to a conclusion that the two-variable and three-variable models are the most appropriate models to be used. Yet the models are all derived from the AS/NZS tests where the air temperatures (dry bulb and wet bulb) are highly correlated. In this case models using both dry and dew point air temperatures may be less accurate as they use redundant data. However, in principle the situation could be reversed in the case of uncorrelated temperature data. In general then, the four-variable model, which is derived from thermodynamic concepts, may give better results.

The models based on 1 Kelvin interval are not always better than those based on 5 Kelvin interval. Indeed, they are better in the Korean test n°3 (errors of about 1% against 5% in the case of the model based on 5 Kelvin interval). However, they are worse in the Japanese test in the case of the 4 variable model.

This section investigates the feasibility of applying the same approach to model a full test that includes a draw-off pattern. In order to do so, the following issues need to be addressed:

• Tank heat losses to the environment; while, tank heat losses can be neglected when compared to the heating capacity of the HPWH during a heat-up phase, they need to be accounted for over a longer time period during which the heat losses represent a significant part of the energy balance;

• Modelling draw-off cycles requires a time simulation of the tank temperature. Therefore, a COP model depending only on temperature variables is insufficient.

The HP’s heating capacity has to be simulated. This can be done via a supplementary model that gives electricity consumption as a function of temperature variables;

• A control-logic model is also required. It should indicate the start and stop times of the HP when operated under a given standard test cycle.

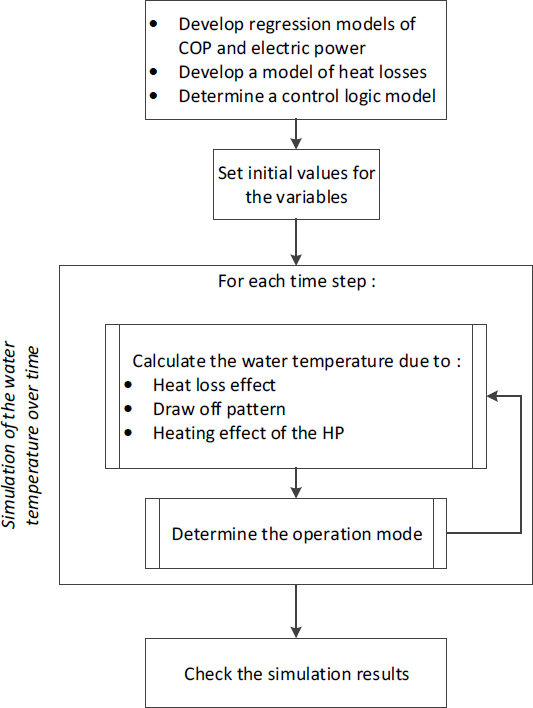
Figure 8 summarises the methodology put forward to model the HPWH operation over a full test cycle including draw-off periods. The following steps are required:

• First, regression models of COP and electric power are developed, using experimental test data measured under limited operational conditions (in our study the AS/NZS test cycle). It is also necessary to develop a heat loss model, from the analysis of a cooling-down period. In addition, a control logic model needs to be determined by observing the operation of the HP;

• Second, the initial variable values are set in accordance with the specifications of the test standard in question;

• The third step is to model the water temperature over time. For each time step, the water temperature is calculated by considering the heat losses, the draw off flow and the HP heating effect. Then, the operational mode of the HP (on or off) is determined;

• Finally, the simulation results are checked by comparison with the measured values.

Figure 8.

Methodology for modelling HPWH operation over a full test cycle

Tank heat losses to the environment. Water tank heat losses is generally modelled as follows:

where T_amb is the temperature of the ambient air surrounding the tank and UA is the tank heat loss coefficient. This approach requires a cooling period (i.e. where the HP is stopped and the water tank temperature decreases due to the heat losses), in order to determine the factor UA. In addition, the variation of T_t must be large enough to allow the UA factor to be accurately determined. For these reasons, the following model is used in place of:

where ΔT_t is the variation of T_t over a period of time Δt, and the factor C_loss can be determined from available test data.

Electric power modelling. As for the COP model development, three electric power models are investigated: a linear model of three variables based on the dry bulb and wet bulb air temperatures and the tank water temperature; a linear model of two variables based on the wet bulb air temperatures and the water temperature and finally the model proposed in the AS/NZS standard [19].

Tank temperature model during a draw off cycle. During a draw-off period, the water tank temperature is considered to be homogeneous in the whole tank. This temperature is the equilibrium of the inlet water supply at a temperature T_supply and the water already in the tank at temperature T_t. Thus, the variation of the tank water temperature over a period of time Δt may be calculated as follows:

where q is the water flow rate and V is the volume of the tank.

Control logic. A model of the control logic is necessary to simulate the evolution of the tank water temperature over time when a draw-off occurs or when the system is under stand-by operation. The control logic indicates the stop/start times of the HPWH.

This methodology is applied to the same HPWH considered in previous parts, in order to develop a model such that regression models are derived using four sets of AS/NZS tests. The heat loss model and control model are determined from the analysis of data taken from a test period where the HPWH is in stand-by operation. The performance of the HP is then simulated according to the US test conditions [21] and the predicted results compared to the measured values. Simulation results are subsequently shown.

Tank heat losses to the environment. Data for four cooling phases are extracted and used to calculate C_loss (one of them shown in Figure 9). All four phases show that C_loss ≈ 0.031 K/min. This value is then used in the subsequent full-test simulations.

Figure 9.

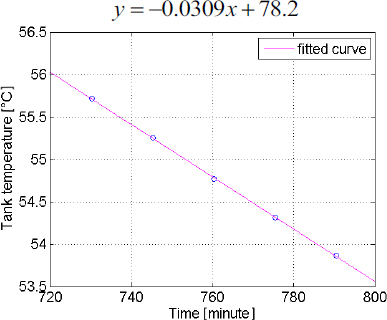
Evolution of the tank water temperature over time for a cooling phase

Electric power modelling. The electric power models obtained are compared to the measured values over the heat-up phase of the US test (Figure 10). The results show that all the models have excellent predictive capability, with errors ranging from 2.2% for both the linear models down to as lows as 0.9% for the AS/NZS model. As it produced the best result the AS/NZS model was selected for the rest of the analysis.

Figure 10.

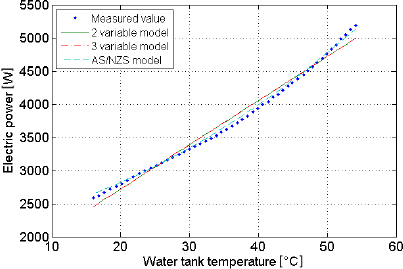
Electric power predictive capability of the correlation models

Control logic. In principle, the electric power drawn by the HP operating in stand-by mode should also be modelled to fully account for the total electric power demand over a complete test. Stand-by power is generally constant and easily measured owing to a stand-by period in the test cycle. In our case, the stand-by power is small enough to be neglected.

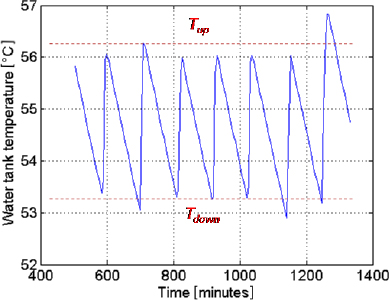
Observations of a period of stand-by operation (shown in Figure 11) indicate that the start/stop of the specific HP is controlled so that the water temperature remains within a narrow temperature band around 55 °C. The control logic is likely to be as follows:

• During a heating phase (when the HP operates) the water temperature increases to an upper set-point temperature T_up = 56.3 °C above which the HP stops;

• During a cooling phase (when the HP is in stand-by mode) the water temperature decreases until it reaches a lower set-point level T_down = 53.3 °C under which the HP restarts.

Figure 11.

Evolution of the tank water temperature over time during a stand-by period

Simulation results during a whole working cycle. Figure 12 shows the evolution of the water tank temperature for both simulated values and experimentally measured values. The simulation values are generally close to the measured values, especially in the heat-up phase. A delay is observed in the simulated stand-by phases (with or without draw-offs) due to inaccuracy in the control model.

Figure 12.

Predictive capability of the full test cycle model developed under the US test standard conditions

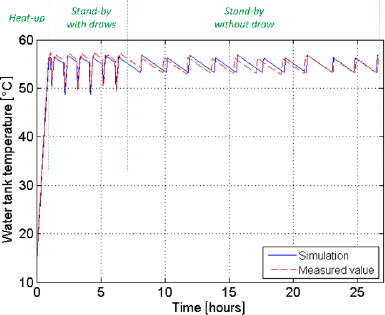
Table 3 compares the simulation results with the measured values. From this it is seen that the heating up time is predicted precisely, with an error as low as 0.6%. The COP error during the heat up phase is small, at about -1%. The temperature loss, defined as the decrease of the tank water temperature due to the heat loss effect and/or the draw-off pattern, has an error of 1.2% over the “stand-by and without draw” period. This indicates that the heat loss model is correct. The error of the temperature loss over the “stand-by with draw” period is higher (-7.5%), probably due to the stratification effect when a drawoff occurs. The COP error in this phase is relatively high (-8.2%), resulting in an error of -6.7% for the whole test.

The results presented above show that it is possible to correctly model a HPWH that only uses a heat pump i.e. that does not also use a back-up electric resistance heater. This section aims to evaluate the feasibility of modelling a heat pump system that includes a back-up electric resistance heater. The experimental test data from a second HPWH are analysed for this purpose.

The following three operational modes are considered:

• Periods when only the heat pump is activated;

• Periods when only the electric resistance heater is activated;

• Periods when both the heat pump and electric resistance are used.

In principle it is necessary to develop a performance correlation model for each of these operational modes. A supplementary model of the control system is also required to be able to predict when each of these modes is operational. This model needs to determine the operational mode as a function of the operating conditions i.e. the air and water temperatures.

The control logic of the HPWH in question is as follows:

• At the beginning of the test period both the HP system and electric resistance heater are used;

• When the water tank temperature reaches a specified limit the resistance heater is turned down/off and only the HP works.

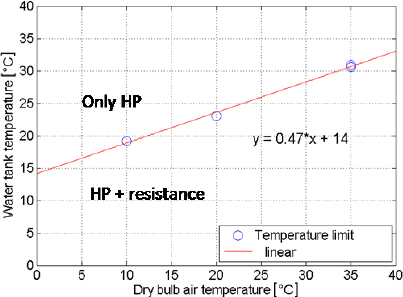
Figure 13 shows the water temperature operational-mode limit (i.e. threshold at which the HPWH operates in either the HP-only mode or HP and resistance heater mode) as a function of the dry bulb air temperature, observed from four sets of experimental tests under the AS/NZS standard. From these, the following linear-correlation function (with a coefficient of determination R² = 0.99) is derived for the threshold tank water temperature T_lim as a function of the dry bulb air temperature T_d: T_lim = 0.47 x T_d + 14

Figure 13.

Temperature limit (thresholds) that separate the two operational modes of the HPWH n°2, as observed from four sets of AS/NZS experimental test data

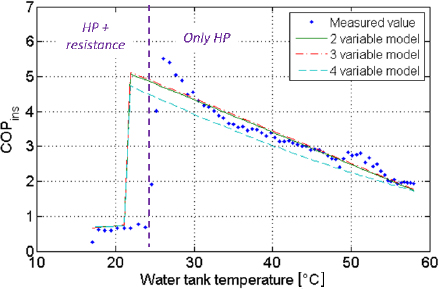
The AS/ZNS test data are also used to develop COP performance correlation models for each operational mode. Three types of models are derived and tested, using two, three and four variables (eq. 8-10). The models obtained are then used to estimate the heat-up phase COP (i.e. without draw off) that would be expected under the Japanese standard test and the estimates are compared to the corresponding test data (Figure 14). It appears that the control model is not completely satisfactory for the Japanese test standard. Indeed, it underestimates the operational mode temperature limit by about 2 K. This error is probably due to the following factors:

• The control logic is not exactly determined from the tank water temperature, but from temperature sensors which are imperfectly correlated with the tank water temperature e.g. the condenser water temperature, or the refrigerant temperature;

• The control logic may be more complicated than a simple linear model of air and water temperatures.

Figure 14.

Predictive capability of the correlation models of the HP n°2 using an electric resistance

The relatively small error in the control correlation model leads to a significant overestimation of the predicted COP compared to the measured COP, with the error ranging from +15 to +22% depending on the model type (Table 4).

The observed error is explicable due to the following considerations:

• The HP-resistance heater operational mode only occurs for a short period of time, but nonetheless represents about 50% of the total energy consumption because the design capacity of the resistance heater is much higher than the capacity of the HP;

• Inaccuracy in the control model results in a significant underestimation of the length of the HP-resistance operational mode such that the time the resistance heater is working in practice is twice as high as the model estimate.

Despite this the COP correlation models are reasonably accurate during the HP mode, especially for the two-variable model.

In principle COP_ins depends on the water temperature surrounding the condenser. Depending on the specific configuration of the HP under consideration, the water temperature surrounding the condenser may be the temperature of the inlet water, the temperature of the outlet water, or even a combination of the two. Due to a lack of appropriate experimental test data, it has been necessary to use the average tank water temperature as the correlating variable for the current study. This is likely to be an appropriate choice when the water being supplied to the condenser is drawn from the water storage tank and the water in the latter is well mixed i.e. is not stratified; and these conditions are more or less satisfied in almost all of the experimental tests investigated in this study. However, it is important to recognise that a model based on average tank water temperature is unlikely to produce reliable results for the following situations:

• When the water supplied to the condenser is drawn directly from the mains water supply (but not from the storage tank), which is true for the Korean tests. In this case, significant error could occur when the inlet water temperature differs appreciably from the tank water temperature, as occurs in Korean test n°1;

• When tank stratification occurs. In the tests studied, this phenomenon is observed in the case of the second HP and only at the beginning of the test (probably due to the activation of the electric resistance heater). The lack of information regarding the exact configuration of the HPWH (i.e. of the geometry of the condenser coil and location of the resistance heater in the tank) and of the inlet and outlet water temperatures does not permit an in-depth study of the impact of this phenomenon on the predictive capability of the model developed.

To avoid these problems, the tank water temperature used in the correlation model should be replaced by a more appropriate variable, depending on the specific configuration of the HPWH.

Due to the lack of appropriate test data, the heat loss model is reduced to a simpler form which is only appropriate in specific conditions (ambient air temperature constant, little variation of the tank water temperature). In order to generalize the methodology for other conditions, a heat loss model based on (eq. 12) would need to be developed.

In addition, the proposed methodology considers that the control logic is the same in all operational modes (heat up, stand-by with or without draw-offs). While this is relatively true for the HPWHs studied, the method may not be appropriate for a HP that uses different control logic dependent on the operational mode. For example, the case when full-load control is used in the heat-up phase and part-load control in the stand-by phase. Additional information on the control system (frequency control, cyclic operation control) used by the specific model of HPWH would then be required to simulate the overall COP. This appears to be a particularly difficult challenge due to the range of differing part load circuitry and control logic used by different manufacturers and it seems unlikely the control logic could be deduced from experimental data. Thus, this limitation could only be overcome if information about the part load circuitry and control logic were to be made available by the manufacturer. In principle, the provision of such information could enable the development of performance models allowing reliable performance prediction over a full test cycle including draw-off patterns.