Renewable energy generation is important due to environmental concerns, increased global demand, and fossil fuel limitations [1]. Sources, such as biomass, solar and hydro energy, have been considered worldwide to reduce dependence on fossil resources. As countries evaluate their energy resources, many have recognized hydrokinetic energy as a significant contributor to their portfolio regarding this commodity [2]. For instance, Ersoy et al. modeled water scenarios in Southern Marocco for renewable energy development [3].

Human development requires access to electricity because it is essential for basic activities such as lighting, refrigeration, and running household appliances [4]. Many rural regions in poor and developing countries lack reliable access to national power grids, and they utilize hydro energy for electrification. For this reason, a decentralized micro-hydro power plant has been developed in North-Eastern Afghanistan [5]. Moreover, [6] examined hydro power-boosting using an underwater power generator based on a gravity vortex siphon. Hydropower has become an attractive source of renewable energy for electricity generation because it is eco-friendly, pollution-free, natural, and favorable for future development. Dependency on fossil fuels can be reduced by increasing renewable energy production [7] and applying small-scale hydro power in locations where available head and discharge are relatively low [8]. The hydropower plant could provide cheap, clean, and reliable electricity [9]. However, hydropower plants are highly water-intensive because large volumes of water evaporate from the increased reservoir surface [10]. Many countries have a significant but unused hydropower potential with head differences below 2.5 m. Standard turbines appear uneconomical because they require large turbine diameters, extensive civil engineering works, and ecological effect considerations [11]. The hydropower plants capture the energy in flowing water and make it useful. Recent studies showed that conventional technologies such as water wheels are suitable devices for low-head sites [12].

Many countries have used irrigation channels for pico-hydro and micro-hydro power plants. Examples include a 0.5 kW electric power generation in Padang Panjang, Indonesia [13], a 160 kW hydropower in Thailand [14], and a micro-hydro in Srilangka [15]. Typically, the micro-hydro power plant capacity is less than 500 kW [16]. Micro-hydro power plants have attracted increasing attention for renewable energy conversion systems due to their simplicity and low-cost installation. As a result, many micro-hydro plants have been successfully developed and tested, as reported by Kamran et al. [17], Jawahar and Michael [18], Nasir [19], and Pigaht and Van der Plas [20]. A stream water wheel seems suitable for a micro-hydro power plant for an irrigation channel.

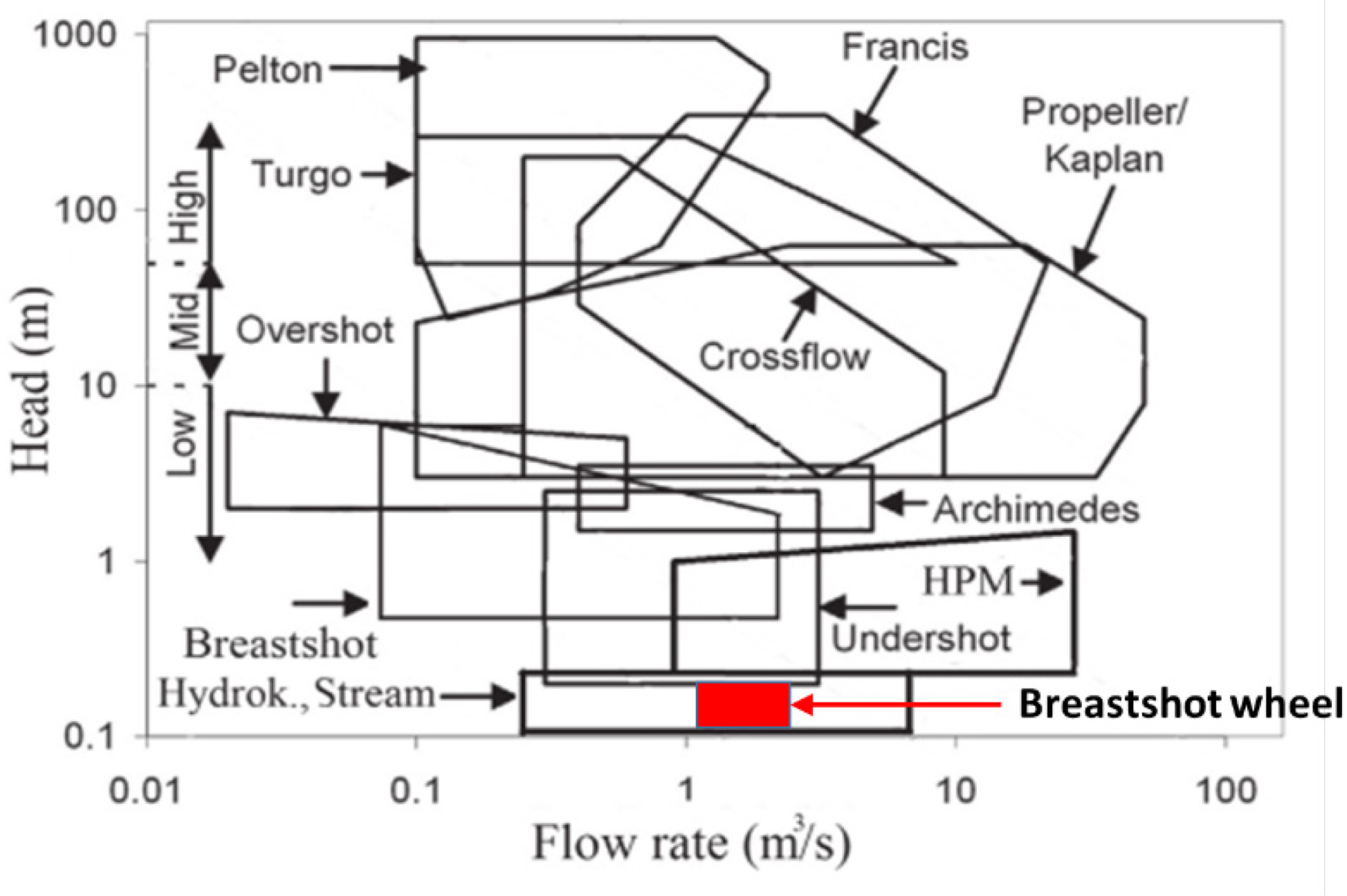
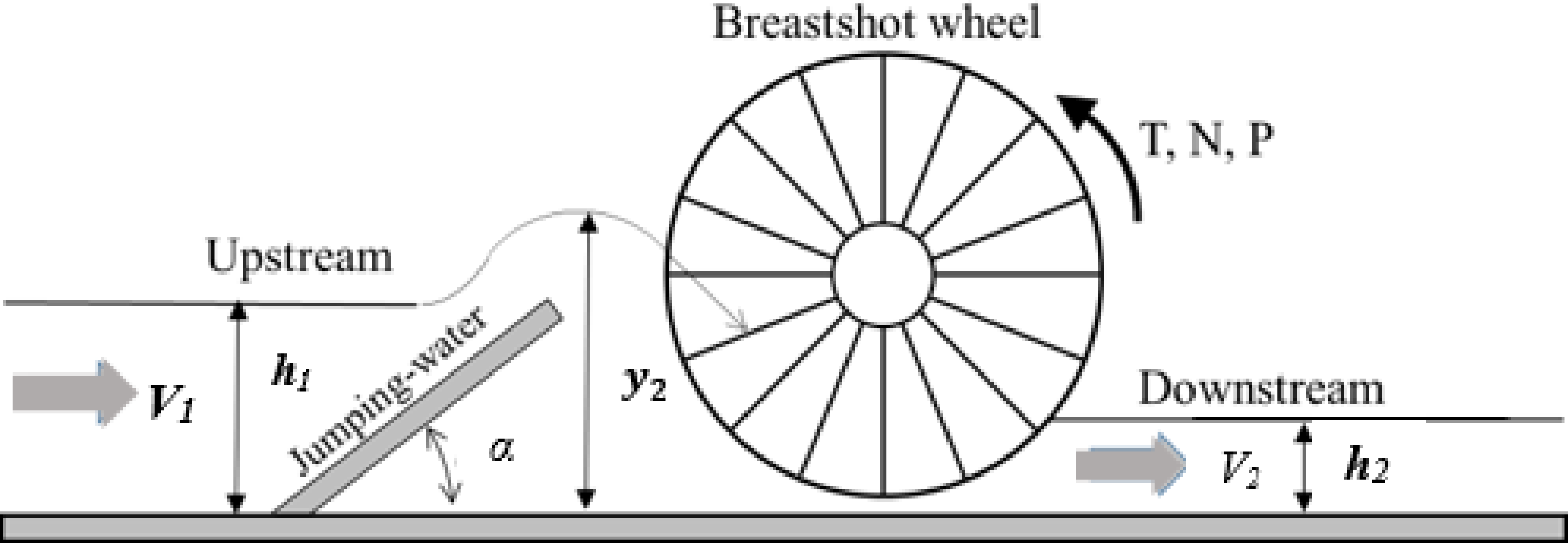
Stream water wheel could be divided into undershot, overshot, and breastshot [21], as shown in the schematic diagram in Figure 1. Many studies examined stream water wheels, such as Quaranta and Ravelli [22], which investigated output power and power losses estimation for an overshot water wheel. The study of [23] also evaluated breastshot water wheels performance using different inflow configurations. Moreover, Quaranta et al.[24] analyzed the efficiency of a traditional water wheel, while the performance evaluation of a breastshot water wheel was experimentally conducted by Vidali et al. 2016 [25] and Muller and Kauppert [26]. Small-hydro power plants intended for low head difference, such as irrigation channels, have also been reported by Bakis et al. [27] and Senior [28]. Other studies performed simulation work to investigate breastshot water wheel performance. For instance, Adanta et al., 2020 [29] simulated the effect of channel slope on breastshot water wheel performance. Budiarso et al. 2018 [30] simulated the impact of bucket shape and kinetic energy on breastshot water wheel performance. A suitable stream water wheel could be selected using the diagram in Figure 2, as suggested by Quaranta [31].

Figure 1.

Categories of the stream water wheel

Figure 2.

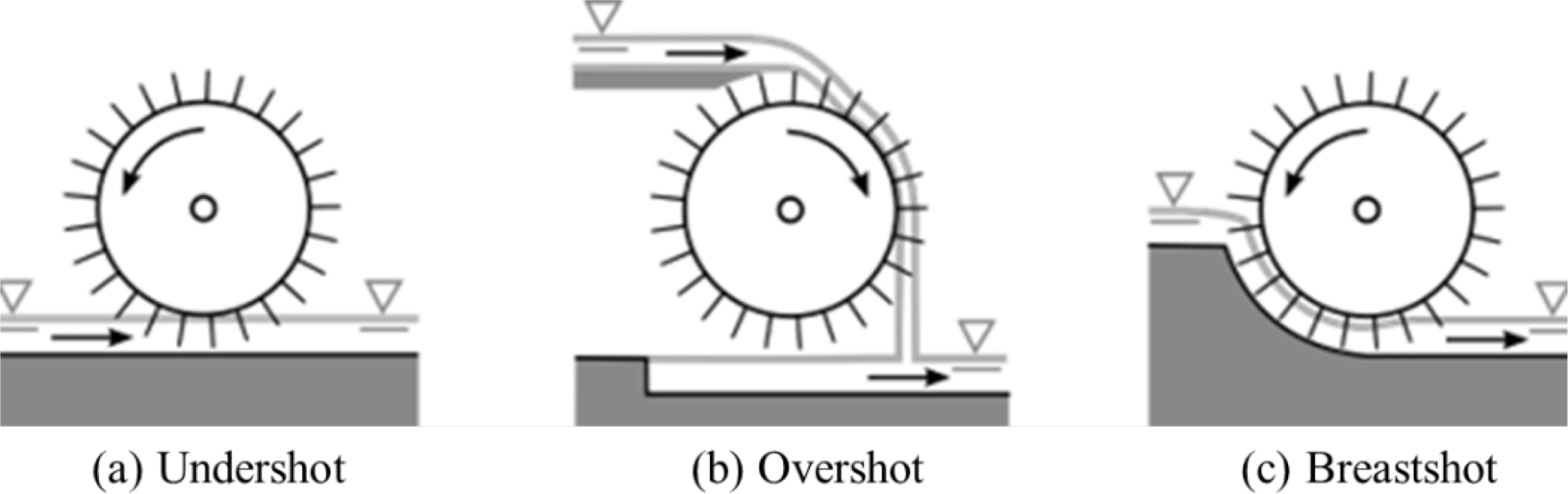
Diagram for selection of water wheel [31]; HPM - Hydrostatic Pressure Machine

The common problem in the micro hydropower plant is operation discontinuity due to low stream velocity in the channel during the dry season. A sustainable operation could be achieved using a water-jumper at the wheel upstream. The blocking effect of the water-jumper may increase the water depth in the conveying channel, increasing the stream’s potential energy. However, the blocking of the flow may affect the velocity of the water downstream and the stream’s kinetic energy. The effect of the water-jumper on depth and velocity results in the availability of the gross head flow.

This study designed the breastshot water wheel for a laboratory-scale open channel. It aimed to investigate the effect of the water-jumper slope angle on the breastshot wheel performance at various upstream velocities. This kind of experiment has not been conducted by any study.

The experimental test rig and measurement devices were set before data collection and analysis.

Experiment Description

The experimental test rig was installed at Institut Sains & Teknologi AKPRIND Indonesia laboratory. Figure 3a shows the experimental test rig comprising a water pump plenum chamber, adapter, jumping-water, breastshot wheel, conveying channel, exit gate, and draught passage. The test rig also has measurement devices, including a digital flow meter, disk brake, load cell, and tachometer, as shown in Figure 3b. The channel is made of a Mild Steel (MS) plate measuring 10 m in length, 0.56 m in width, and 0.4 m in depth. The water-jumper with an adjustable angle (α) was attached at the wheel’s upstream. The breastshot wheel was hand-made from MS plate, measures 0.8 m in diameter, and has 16 galvanized blades, each measuring 0.4 m and 0.5 m in width and length, respectively. The stream velocity was measured using a digital flow meter, while a tachometer measured the wheel’s rotational speed. Furthermore, a disk brake dynamometer was used to obtain the wheel’s torque. The experiment was conducted at stream velocities of 1.1, 1.2, 1.3, 1.4, 1.5, and 1.6 m/s and water-jumper slope angles of 5°, 10°, 15°, 20°, 25°, 30°, 35°, and 40°.

Figure 3.

Schematic diagram (a) and photograph (b) of experimental test rig; dimensions are given in mm

Data Analysis

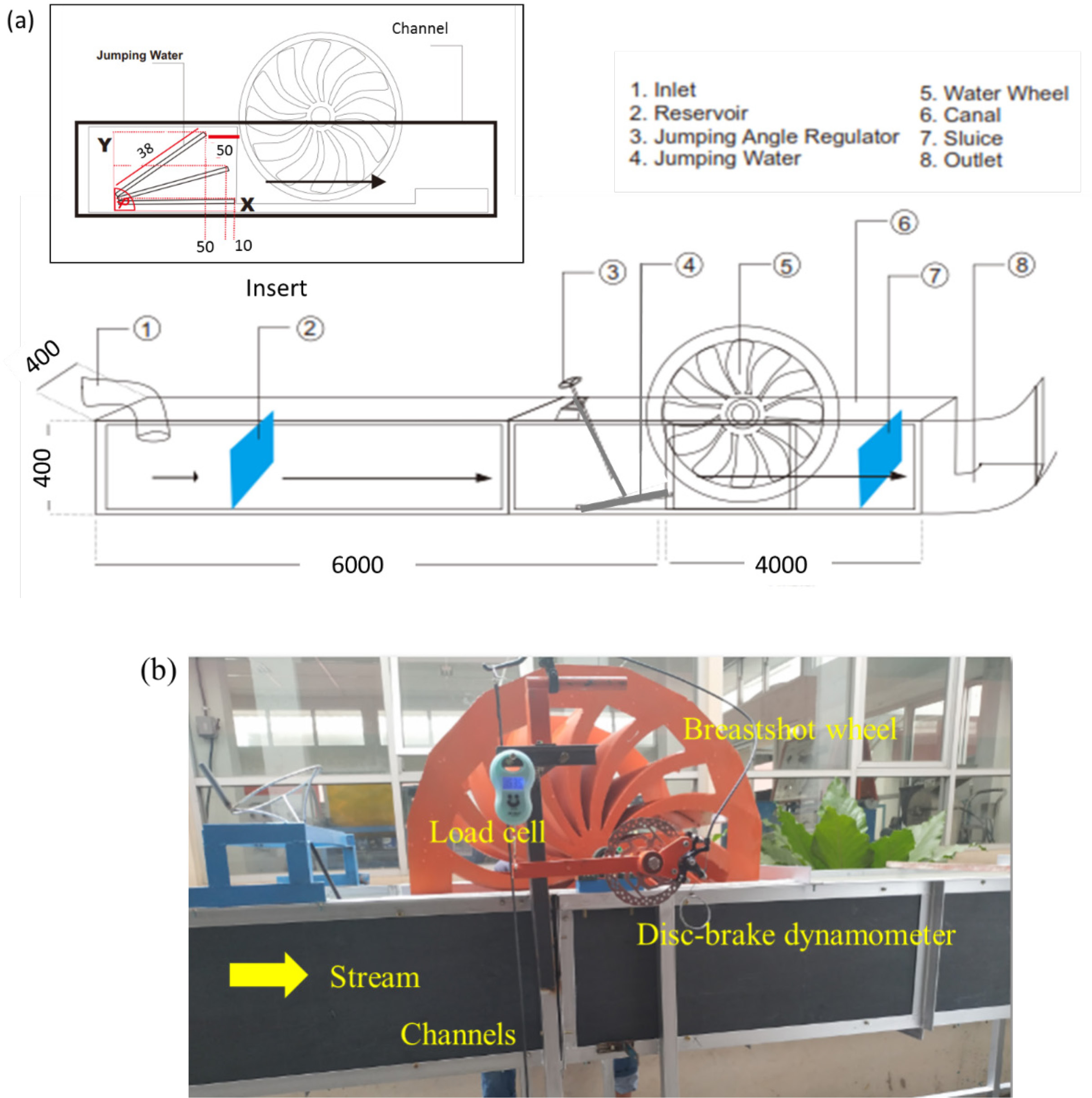
Figure 4 shows a schematic diagram of a breastshot wheel in the channel without a water-jumper. Water flows with velocity v₁ and depth h₁ at the upstream and v₂ and h₂ at the downstream. The diagram governs the flow’s head gross equation. Head gross would be converted to rotate the wheel to produce mechanical energy. In this case, the flow head gross is the difference between the energy head comprising pressure, kinetics, and upstream and downstream potential, as shown in Eq. 1. Since the upstream and downstream pressure is the same (p₁ = p₂) and the channel is horizontal (z₁ = z₁), Eq. (1) simplifies as Eq. (2):

$H_{gr}=\left\{\frac{p_1}{\gamma }+\frac{{\upsilon }_{{}_1}^2}{2g}+(z_1+h_1)\right\}-\left\{\frac{p_2}{\gamma }+\frac{{\upsilon }_{{}_2}^2}{2g}+(z_2+h_2)\right\}$ (1)

$H_{gr}=(\frac{{\upsilon }_1^2-{\upsilon }_2^2}{2g})+(h_1-h_2)$ (2)

Where H_gr is the head gross [m], v is the stream velocity [m/s], h is the stream height [m], g is the gravitational acceleration (9.81 m/s²), and subscripts 1 and 2 indicate the wheel’s upstream and downstream, respectively.

Figure 4.

Schematic diagram of the wheel in the channel without water-jumper

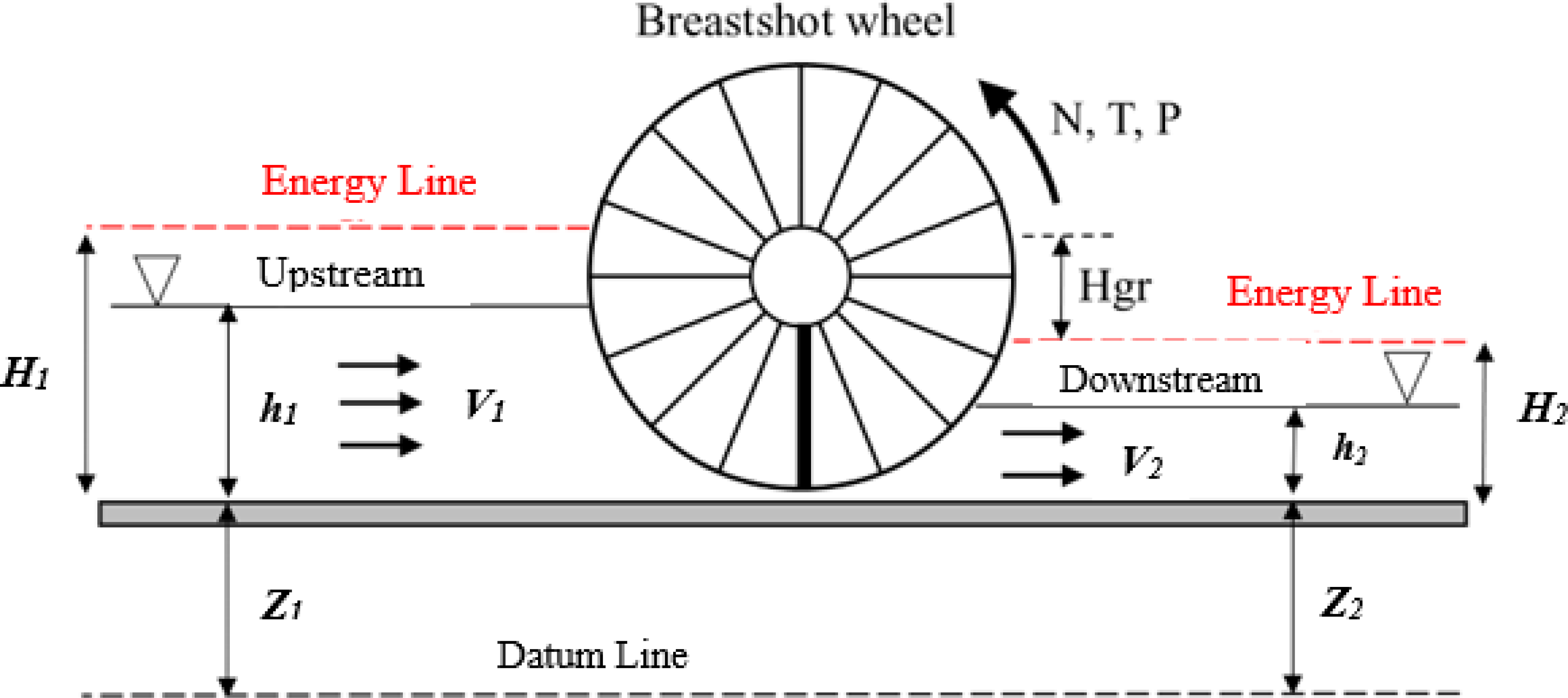
Figure 5 shows the schematic diagram of the water wheel installed in the channel with a water-jumper. The upstream head (h₁) was effectively replaced by water jumping height (y₂) following the hydraulic jump theory [32]. Therefore, the flow’s head gross equation with the water-jumper changes to:

$H_{gr}=\left(\frac{{\upsilon }_1^2-{\upsilon }_2^2}{2g}\right)+(y_2-h_2)$ (3)

Based on hydraulic jump theory and assuming the use of a water-jumper with a length of 0.4 m and slope angle α, the height of hydraulic jump at the wheel’s upstream becomes:

$y_2=2.2h_1+(0.4sin\alpha -h_1)$ (4)

By substituting Eq. (4) into Eq. (3), the head gross for the channel with water-jumper is given by Eq. (5):

$H_{gr}=\left(\frac{{\upsilon }_1^2-{\upsilon }_2^2}{2g}\right)+\left\{\left(\left(2.2\times h_2\right)+\left(0.4sin\alpha -h_1\right)\right)-h_2\right\}$ (5)

Figure 5.

Schematic diagram of the wheel in a channel with water-jumper

Comparing the water-jumper with the broad caster weir [32], the discharge coefficient is calculated using Eq. (6). The volumetric flow rate of the channel is derived from the flow rate equation, Eq. (7).

$C_d=1.125{\left(\frac{1+\left(y_2-h_1\right)/0.4\sin \alpha }{2+\left(y_2-h_1\right)/0.4\sin \alpha }\right)}^{1/2}$ (6)

$Q^{\prime }=C_d\times b\times {\upsilon }_1\times h_1$ (7)

Substituting Eq. (6) into Eq. (7) and assuming the water-jumper width b = 0.56 m, the volumetric flow rate becomes:

$Q^{\text{'}}=0.63{\left(\frac{1+\left(y_2-h_1\right)/0.4\sin \alpha }{2+\left(y_2-h_1\right)/0.4\sin \alpha }\right)}^{1/2}\times {\upsilon }_1\times {\upsilon }_2$ (8)

Once the head gross and volumetric flow rate are known, input hydraulic power to the water wheel is calculated using Eq. (9), where ρ is the density of water (1000 kg/m³).

$P_{in}=\rho g{Q}^{\text{'}}{H}_{gr}$ (9)

The wheel’s torque, output power, and efficiency are obtained using Eqs. (10), (11), and (12), respectively.

$T_a=m_b\times g\times l$ (10)

$P_{out}=\frac{2\times \pi \times N_a\times T_a}{60}$ (11)

$\eta =\frac{P_{out}}{P_{in}}\times 100\%$ (12)

where T_a is the torque [N m], m_b is the mass of the load cell [kg], l is the distance from the wheel's axis to the load cell (0.4 m), P_in is the output power [W], and N_a is the rotational speed [rpm].

This study analyzed the effect of slope angle on gross head, hydraulic power, torque, output power, and efficiency.

Effect of slope angle on the gross head

Figure 6 shows the effect of the water-jumper slope angle on head gross at different upstream velocities. The head gross increases significantly at slopes above 10º (the height of the hydraulic jump increases with slope, resulting in increased potential and gross head). Figure 6 also shows that the gross head increases with upstream water velocity for the same jumper angle due to increased hydraulic jump.

Figure 6.

Gross head (Hgr)as a function of the slope angle of water-jumper

Effect of slope angle on hydraulic power

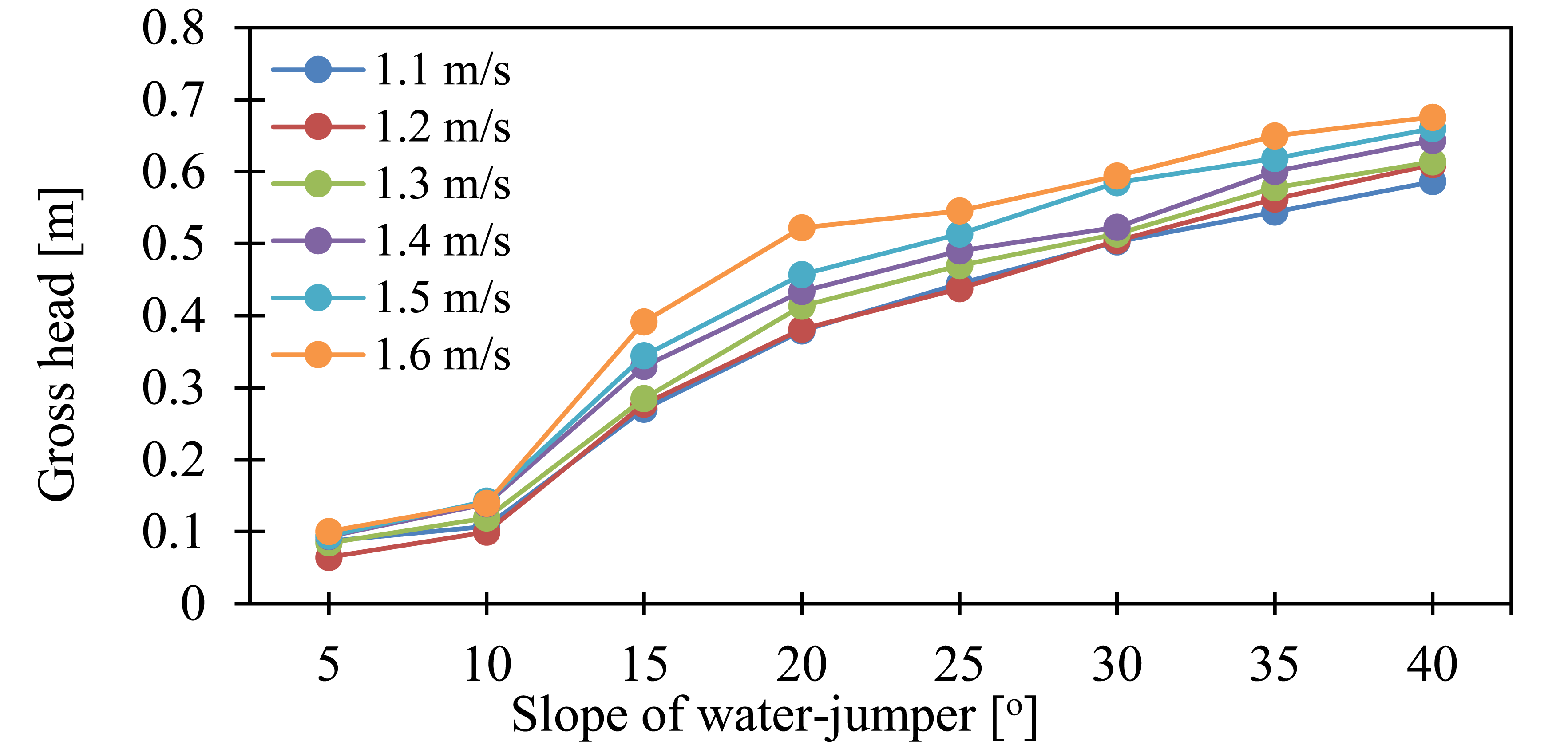
Figure 7 shows the effect of the water-jumper slope angle on the wheel’s hydraulic power. At the same upstream velocity, the hydraulic power increases from 15º and steps up significantly at 10º–20º. The hydraulic power is influenced by discharge and gross head, and its graph is similar to the trend of the gross head and discharge, which increase with the water-jumper slope angle. The hydraulic power is enhanced with increased upstream velocity for a particular slope angle.

Figure 7.

Hydraulic power (P_in) as a function of the slope angle of water-jumper

Effect of slope angle on torque

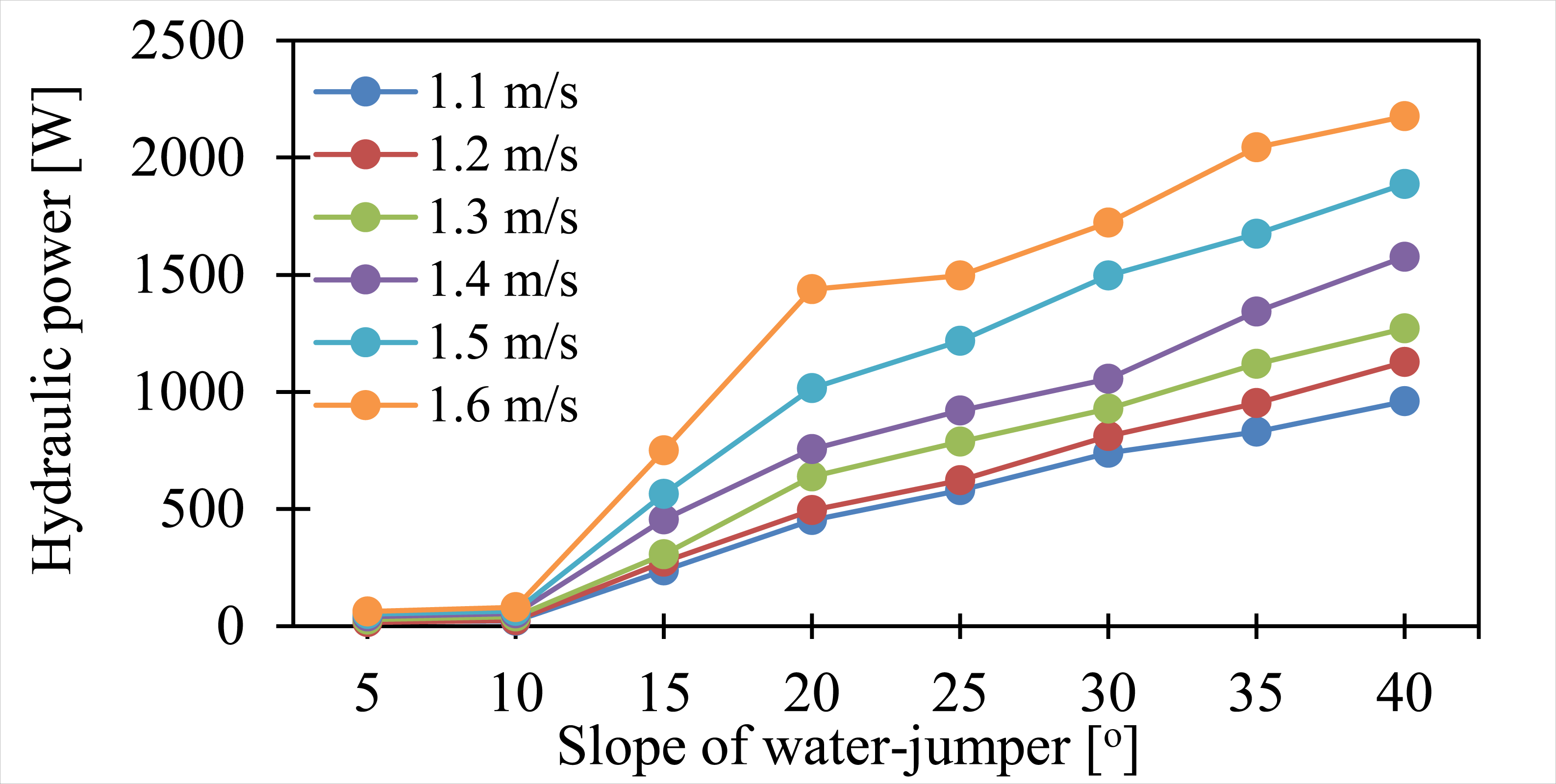
Figure 8 shows that the torque increases with slope angle. It means that a larger angle produces more power to improve the torque. From Figure 7, the torque and hydraulic power trends are similar.

Figure 8.

Torque (T_a) as a function of the slope angle of water-jumper

Effect of slope angle on output power

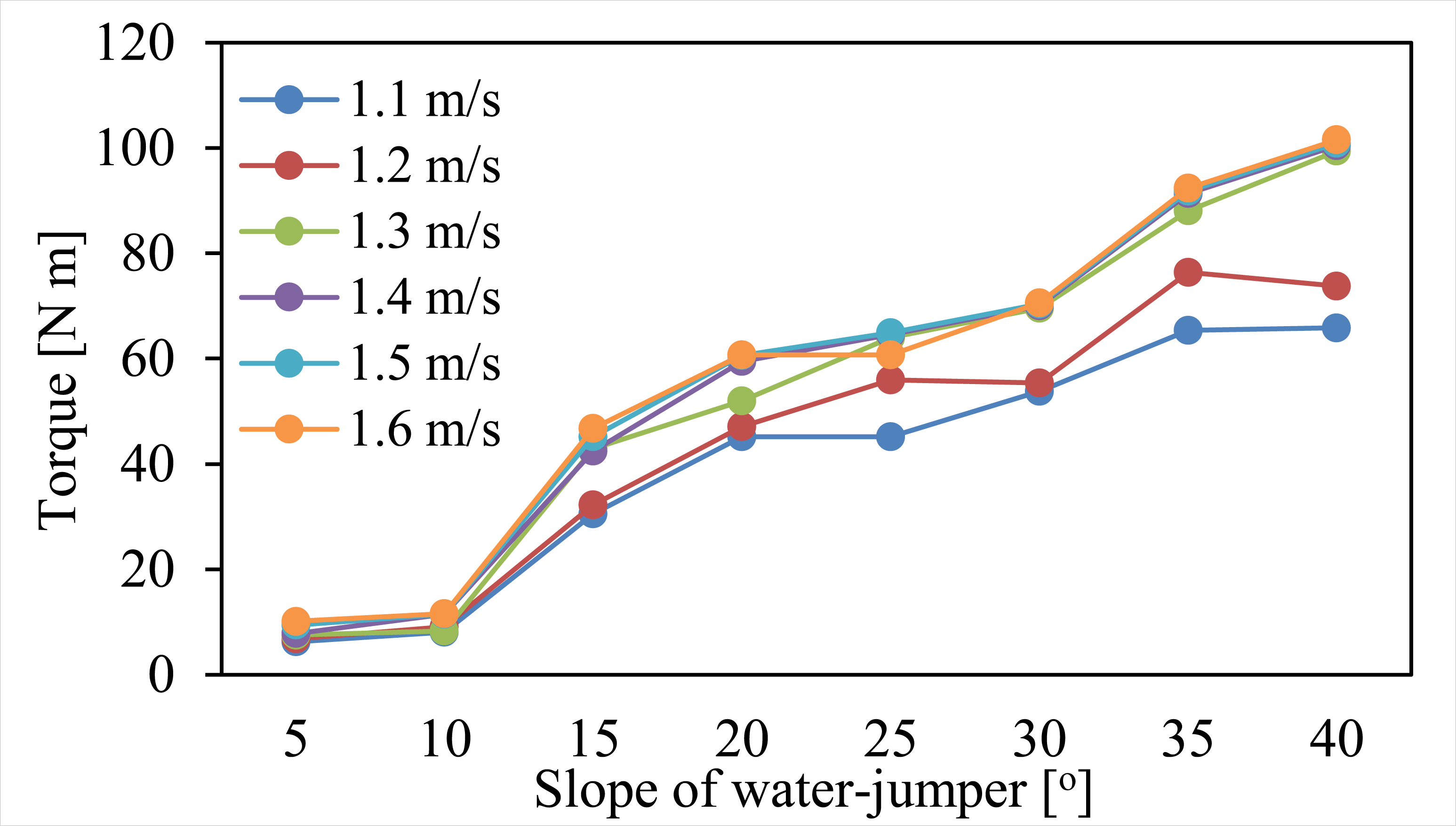
Figure 9 shows the effect of slope angle on the breastshot’s actual power, which increases significantly at 10º–20º at all upstream velocities. The actual power remains the same or decreases at a slope angle greater than 20º due to decreased breastshot’s rotational speed (the wheel’s output power is directly proportional to rotational speed, as shown in Eq. (11)). However, a different trend of output power at a slope angle higher than 30º is observed for a stream velocity of 1.6 m/s. The output power decreases significantly from 35º to 40º, even as the hydraulic power increases, due to more momentum losses at 35º to 40º for a higher stream velocity of 1.6 m/s.

Figure 9.

Output power (P_out) as a function of the slope angle of water-jumper

Effect of slope angle on efficiency

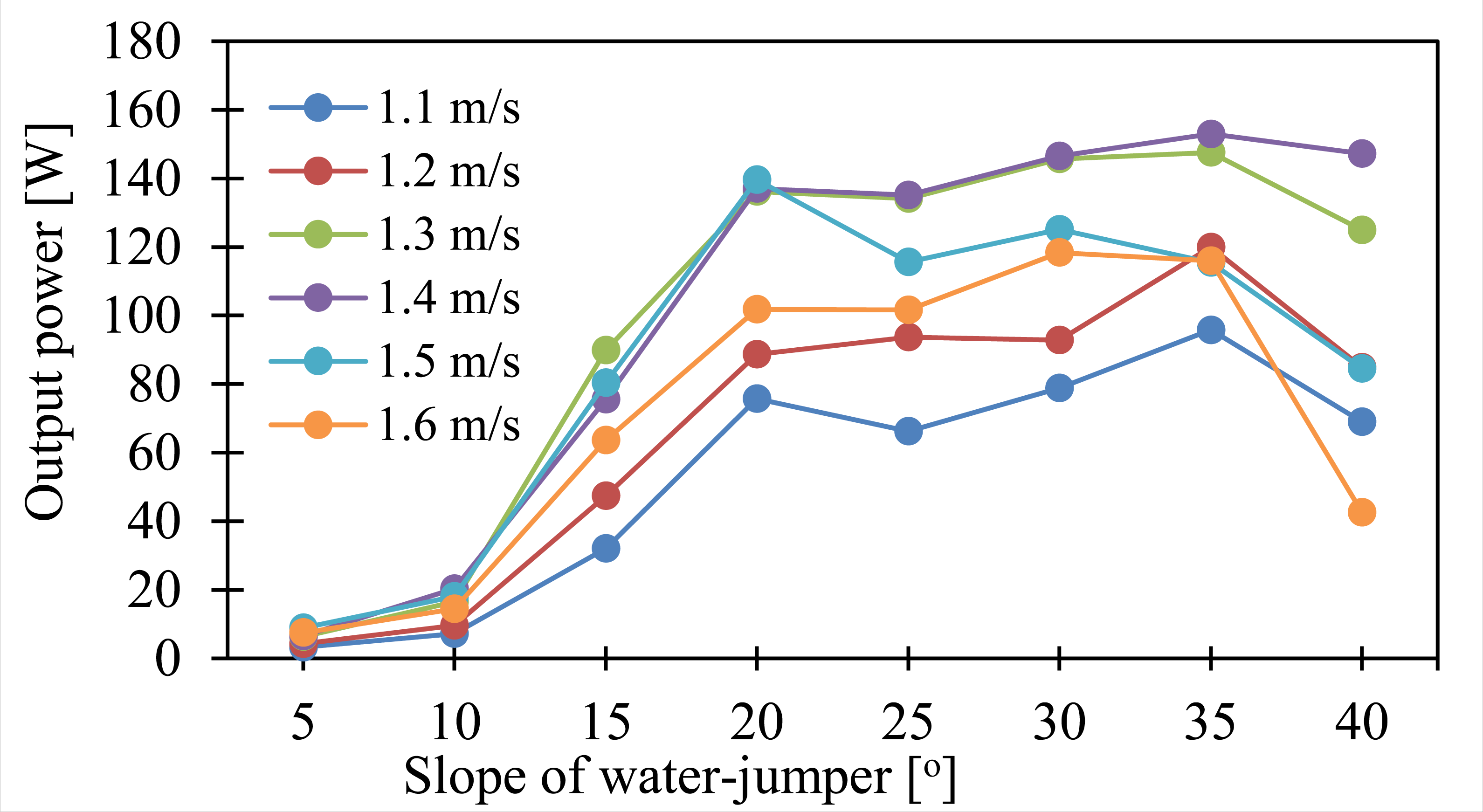
Figure 10 shows the effect of slope angle on the wheel’s efficiency, which becomes highest for each upstream velocity at 10º. At a slope angle of 10º, maximum efficiency of 41.73% is obtained for an upstream velocity of 1.3 m/s. The efficiency steps up from 5º and reaches a maximum value at 10º, but decreases at higher slope angles. The water-jumper slope angle higher than 10º is ineffective in improving breastshot performance. Therefore, the slope angle must be set at 10º when the stream velocity varies from 1.1 m/s to 1.6 m/s.

Figure 10.

Efficiency (η) as a function of the slope angle of water-jumper

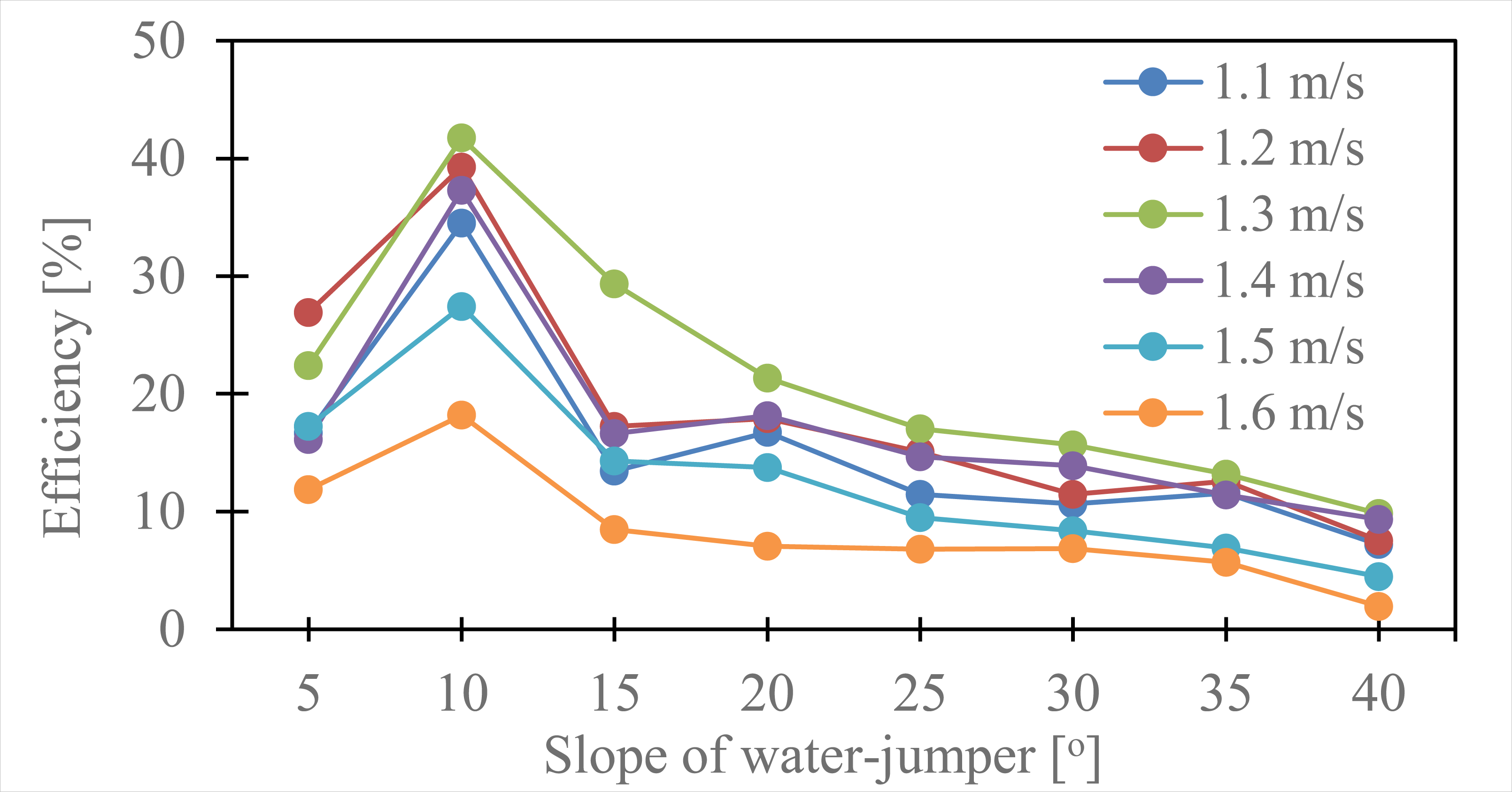
This study aimed to investigate the effect of water-jumper slope angle on breastshot water wheel performance at low stream velocities. The results showed that a water-jumper increases gross head, torque, and hydraulic and output power. However, the highest efficiency is achieved at a slope angle of 10º and stream velocity of 1.3 m/s. The water-jumper significantly affects the water wheel performance, specifically when stream velocity is lower than 1.3 m/s. The hydraulic power is influenced by discharge and gross head, which increase with the water-jumper slope angle. Significant momentum losses occur at the wheel for stream velocity higher than 1.3 m/s, decreasing the breastshot’s output power and efficiency, even as hydraulic power increases. Therefore, a water-jumper could be useful in maintaining continuous breastshot wheel operation in the irrigation channel during the dry season when the slope angle is set at 10º.

The authors are grateful to Institut Sains dan Teknologi AKPRIND Yogyakarta for the financial support to pursue a Doctoral program in the Mechanical Engineering Department of Universitas Diponegoro, Central Java, Indonesia.