Access to electricity is nowadays recognized as an essential condition for economic, social and political development. The weakness in the field of electricity supply is a major obstacle to social and economic development in Africa, particularly in Sub-Saharan Africa [1]. Despite its enormous renewable energy potential, Africa remains the continent with the lowest electricity production and access to electricity networks [2]. To increase the population's access to electricity, several African countries are multiplying renewable energy initiatives. One of these is Togo, which aims to ensure universal access to electricity for all Togolese between now and 2030 through an intelligent combination of national grid extension and off-grid technologies (microgrids, mini-grids and solar kits). This goal is aligned with the objectives of its new national development plan (NDP 2018-2022) [3]. Since then, Togo has increased the use of photovoltaic energy through several photovoltaic energy plant projects inauguration to improve and increase access to electricity by the population.
Despite these efforts, electricity is still considered a luxury in some rural areas today. Because of this situation, mobile network operators continue to deploy thermal generators as the primary energy source for their sites in rural areas when serving them with telecommunications networks. These thermal engines have very high maintenance costs, and are the sources of greenhouse gas emissions. They require regular fuel supplies, while roads in these areas are often unmotorable during the rainy seasons. Consequently, there is frequently a lack of services for long periods during the year because of lack of energy. In addition, citizens in these areas are very resourceful in recharging their cell phone batteries by many different means (car batteries, transporting many phones to neighboring towns sometimes located tens of kilometers away).
To overcome these difficulties caused by the absence of electrical networks in rural areas, microgrids composed of photovoltaic panels as the primary source with which generators are associated, and storage batteries, are suggested as an alternative. Indeed, these microgrids can serve as links between universal telecommunications and electrical energy services access because, surplus productions can be exploited to provide electricity to local populations.
This new model made of multiple sources and multiple loads will induce difficulties in the planning and operation process, because of the stochastic nature of solar energy, and the electricity demand of the local population. In order to ensure stable long-term operation under various load conditions, the microgrids must have an optimal energy management system.
In the literature review, there are several recent research contributions that are focused on the optimization problems of microgrids. In the research presented in [4] intelligent energy management and control systems (EMS) can enhance the efficient use of electricity and maintain the balance between supply and demand by using energy forecasting and storage technologies. These EMSs require optimization algorithms to minimize the energy cost. For this purpose, the author [5] used two optimization techniques, namely Particle Swarm Optimization (PSO) and Differential Evolution (DE) to manage the energy produced by a power plant composed of a diesel generator, a natural gas-fired generator, a photovoltaic (PV) generator and a wind generator. The effectiveness of the two optimization algorithms was shown through tests in grid-connected and islanded modes to demonstrate the effectiveness of the optimization algorithms. In grid connected mode, the optimal use of grid during on- and off-peak hours achieved the lowest operational cost. Likewise, for islanded mode of operation, the use of all generators to match the load demand achieved the lowest operational cost. The authors in [6] used PSO algorithm to optimize the network for improved microgrid performance. Simulation results in MATLAB/Simulink environment showed that the proposed model is able to reduce the prediction errors. In [7], the authors used simulation software Hybrid Optimisation Model for Electric Renewables (HOMER) to analyse and optimise the of grid-connected PV, wind turbines, and battery packs for Syiah Kuala University. The techno-economic performance and optimisation analysis showed that connecting solar PV and wind turbines to the local grid contribute up to 82% of the electricity required. MATLAB software was uses by the author in [8] to design a solar off-grid PV system for supplying the required electricity to residential units in Malaysia. The results showed that the PV array can meets the desired load profile during the day, and the storage units (battery) at night can meet the desired load. The software MATLAB/SIMULINK was used by [9] to implemented the platform with the solar radiation on a sunny and wintery day. They presented a detailed design of an independent solar home system for a typical residential building in the southern part of Bangladesh, Khulna. Simulated results indicate that the proposed model meet the load demand and show satisfactory performance. In [10], the authors proposed a method based on genetic algorithms for optimisation of an off-grid wind/PV/battery power system for remote water desalination system. Their results showed the weather data in the selected site is very helpful for a long period of energy production to feed such systems.
Other artificial intelligence techniques have been used by other authors for intelligent energy management and control systems (EMS). These include [11] who proposed an Internet of Things (IoT) Energy Management System, realised via the Remote XY platform for a standalone photovoltaic system with storage batteries. Novel constant battery operating algorithm is proposed for EMS of the System. All the loads are connected through IoT and hence their status maybe monitored and controlled from remote location. The authors in [12] chose as a solution the application of a recent nature-inspired metaheuristic optimization algorithm, called delayed particle swarm multimodal optimization. The proposed system comprises photovoltaic panels (PV), wind turbines (WTs), battery storage systems, and diesel generators (DGs) in a fishing village that is located in the coastal city of Essaouira, Morocco. The results of the optimization show that the solution is very promising and using renewable energy is a good alternative to enhance energy access in remote areas. In the [13], the authors presented a sizing optimization methodology of panel and battery capacity in a standalone photovoltaic system with lighting load. Performance of the system is identified by performing Loss of Power Supply Probability (LPSP) calculation. The results show that design space approach offers several advantages than using other methods. The authors in [14] proposed a tool for the design of stand-alone rural electrification systems based on photovoltaic technologies, including both microgrid or individual supply configurations. This tool is formulated as a Mixed Integer Linear Programming model including economic, technical and social aspects was used to design electrification systems in three real communities. The results highlight the benefits of the developed tool. The authors in [15] proposed a techno-economic analysis of commercial-scale photovoltaic (PV) systems deployed in five selected cities in Punjab, Pakistan for commercial agricultural farms. For the PV system design, the K-means approach was used to cluster data from 93 farmers into nine clusters with similar electrical consumption. The result of this study demonstrates that renewable energy sources are a more dependable, cost-effective, and financially viable solution than traditional energy sources for supplying electric energy to agricultural farms.
Microgrids can operate in synchronization with the general grid or in islanded mode with storage solutions and an intelligent control system. In a grid-interfaced system, power management is essential to maintain system reliability. Thus, the authors in [16] used the Grey Wolf Optimizer (GWO) algorithm to model and build a unique controller for a grid-interfaced PV system to achieve optimal power management in the system. The performance of the system was evaluated and the results were compared with existing control techniques such as BSO and PSO. The proposed model’s simulation results show that the system’s efficiency improved. The feasibility of an off-grid PV system design for the greenhouse was analysed in Sabha City, Libya by [17]. Their results show that the PV generation system is competitive compared with diesel-powered installations on the basis of the available incident solar radiation in that site. In the [18], the authors presented an analysis component required for the design of a stand-alone photovoltaic system that will power all electric appliances at a medium-energy-consumption residence in Hilla City, Iraq. It was show that, the process of designing, selecting and calculating the ratings of the equipment’s employed in the system depends on a variety of factors such as geographical location, solar irradiation, and load requirements. An economic analysis of a PV system integrated with WT, fuel cells (FC) and an electrolyser with a hydrogen tank working as the energy storage was presented by [19]. The presented results showed the effectiveness of the proposed approach at the optimal configuration and the limits of investment costs necessary to build the system in detail. To overcome the absence of the area-specific generation capacity and economic feasibility data for solar energy, the authors in [20] assessed the potential and economic viability of utilizing an off-grid solar PV system for rural electrification in the Punjab province of Pakistan. The research results reveal that there is an excellent solar irradiance in the rural areas of Punjab for electricity generation. The authors in [21] optimised an off-grid hybrid solar/wind energy system, considering two energy storage devices: hydrogen (as a form of chemical storage) and batteries (as a form of electrochemical storage), using three optimisation algorithms (simulated annealing, harmony search and chaotic search) for Island electrification in Iran. The optimization results demonstrate that a wind and solar energy based hybrid system with electrochemical storage offers more cost effective and reliable energy than a hybrid system for renewable energy with chemical storage. The studies of [22] showed the technical–economic, operational and environmental feasibility of four off-grid hybrid power systems to supply energy to the Cerrito de los Morreños community in Ecuador. In [23], the authors presented a design and analysed the off-grid photovoltaic (PV) system for village electrification in a rural site in Iraq. Their study confirmed that the use of PV systems for electrification is suitable for long-term investments with the cost of $ 0.51/kWh.
In recent times, many researchers have presented various works on the design of standalone PV (SPV) systems. The stand-alone diesel generator and photovoltaic/diesel configurations showed higher Net Present Costs, instability problems and higher CO2 emissions. The authors in [24] examined hybrid renewable energy power production systems with a focus on energy sustainability, reliability due to irregularities, techno-economic feasibility, and being environmentally friendly. The goal functions, constraints from design, system components, optimization software tools, and meta-heuristic algorithm methodologies were highlighted in this work. In [25], the authors proposed an interesting methodology for the optimal sizing of stand-alone Photovoltaic (PV) and Wind Generator (WG) systems for residential household. The proposed methodology aimed to select the components of the system from the commercially available in the market that is guaranteed to minimise the total system cost of 20 working years. The simulation results verify that hybrid PV/WG systems feature lower system cost compared to the cases where either exclusively WG or exclusively PV sources are used. The authors in [26] presented a study a design and economic comparison of the two most feasible methods of solar power production for rural areas in Afghanistan. In the first method, a stand-alone Solar Photovoltaic (PV) system has individually been considered in every single house of a village. In the second method, energy for the whole village is produced by a micro solar power station in a centralized manner and then distributed through a 0.4 kV islanded Mini grid all around the village. The result indicates that implementation of the centralized Mini grid is not only best affordable but also more viable and can create other socio-economic opportunities. The authors in [27] presented a detailed design of a stand-alone photovoltaic system based on a practical approach for the all-weather condition. An elaborate cost analysis considering the entire life span of solar PV module installation and maintenance was considered. The results show that the proposed system can be used in rural areas where the electricity grid is not available.
In order to solve the multi-objective optimization problem to simultaneously minimize the operating cost, pollutant emission level as well as the power loss of the conversion devices, many authors proposed a new daily energy management system in a microgrid. Thus, authors in [28] used the fuzzy logic approach to satisfy the multi-objective optimization dispatch problem to simultaneously minimize the operating cost, pollutant emission level as well as the power loss of conversion devices. The aim is to satisfy system load and technical constraints by ensuring high penetration of renewable energy and optimal scheduling of battery storage system charge/discharge based on a fuzzy logic approach. The obtained simulation results demonstrate that the proposed methodology guarantees a real time operation control and optimization dispatch of MG, considering technical, economic and environmental tasks simultaneously. In the research presented in [29], the genetic algorithm was used to evolve the microgrid comprising photovoltaic arrays, diesel generators and storage systems configuration towards an optimum and allows visualizing the trade-offs between all the design goals. The multi-objective optimisation method was proposed to design these microgrids considering three objectives: economical, environmental and reliability. The results have shown that reliability can be optimised with a high level of renewable integration with little extra cost.
Previous research has shown that microgrids with PV panels and batteries provide substantial cost savings compared to the alternative of consuming only electricity from the grid. The authors in [30] focused their research in this direction by investigating the economic viability of a PV-only system and a PV + battery system based on the pricing scenario. In order to do that, they analysed residential microgrid projects under seven tariff designs in seven countries of the European Union (Belgium, Greece, Italy, Denmark, Finland, Germany and Spain), and compare the economic viability of photovoltaic systems with and without batteries. The findings show that the conditions most favourable to batteries are given by a capacity tariff scheme allowing price arbitrage. The authors in [31] demonstrated that batteries are the most common and economical storage devices in the medium power range and require a DC-DC bidirectional converter to allow energy exchange between the battery and the rest of the system. To this end, they implemented converters with Loss-Free Resistor (LFR) behavior to manage the three constituent blocks of a nanogrid namely, photovoltaic energy, AC mains connection, and bidirectional battery operation. In [32], the authors performed Optimization and techno-economic analysis to design the hybrid renewable energy system by using HOMER Software to provide uninterrupted power and meet different load demands of different communities in Doddipalli village, Chittoor, Andhra Pradesh, India. The results showed that the proposed system is more economical when solar energy becomes the primary source and is integrated with the battery. The authors in [33] used HOMER software as a tool for optimization analysis by investigating the techno-economic and environmental performance of photovoltaic (PV)/diesel/battery HES. The results show that variations in critical parameters, such as battery minimum state of charge, time step, solar radiation, diesel price, and load growth, exert considerable effects on the performance of the proposed system.
Hybrid renewable energy sources are sustainable and eco-friendly and challenge the alternative sources of conventional energy production facilities. Thus, the study of [34] addresses the situation of solar photovoltaic power in Libya, the use of solar energy, and proposes strategies adopted by Libya to encourage future applications of solar photovoltaic energy and electricity generation. They investigated an opportunity to exploit solar photovoltaics to meet the deficiency in energy demand and by the affordable way.
It is clear from this literature review that previous academic research has extensively examined energy flow management in microgrids as well as management algorithms.
According to some analysts, Africa can count on two gigantic reservoirs of development. The first is its potential for green electricity production, particularly via solar energy, which is still largely under-exploited. The second is the development of the telecommunications sector, particularly mobile telephony, whose network coverage has extended far beyond the electricity network and which is at the origin of the main developments on the continent [1]. The novelty in this work is to see how effective management of energy flows in microgrids based on photovoltaic energy in rural areas in developing countries, can foster the convergence of universal access to telecommunications and electricity services in order to contribute to the achievement of Sustainable Development Goals SDGs 7 and 9c. Thus, the Particle Swarm Optimization (PSO) algorithm is used to provide intelligent and optimal management of multiple sources in real time, to keep the continuous supply of electricity to operators' sites, and to use the excess production to provide electricity at a lower cost to the local population. This optimization algorithm is required to determine the minimum Levelized Cost Of Energy (LCOE), the Loss of Power Supply Probability (LPSP), and the Maximum Renewable Factor (MRF) to show the effectiveness of the proposed solution.
This work presents first, the current situation at the telecommunications operators' sites in rural areas, and gives an overview of the new energy model studied. The second part is focused on the study and modeling of the different components of the microgrid. The third part treats the choice of the intelligent energy management model. Finally, the case study, the results of simulations are presented followed by the conclusion and the perspectives.
Mobile telecommunications networks need permanent electrical power to provide services. However, in the African context, where the electricity grid is not available in rural areas, network operators often use thermal generators as their primary power source in these areas, as shown in Figure 1.
Operators’ sites in rural areas with low population density
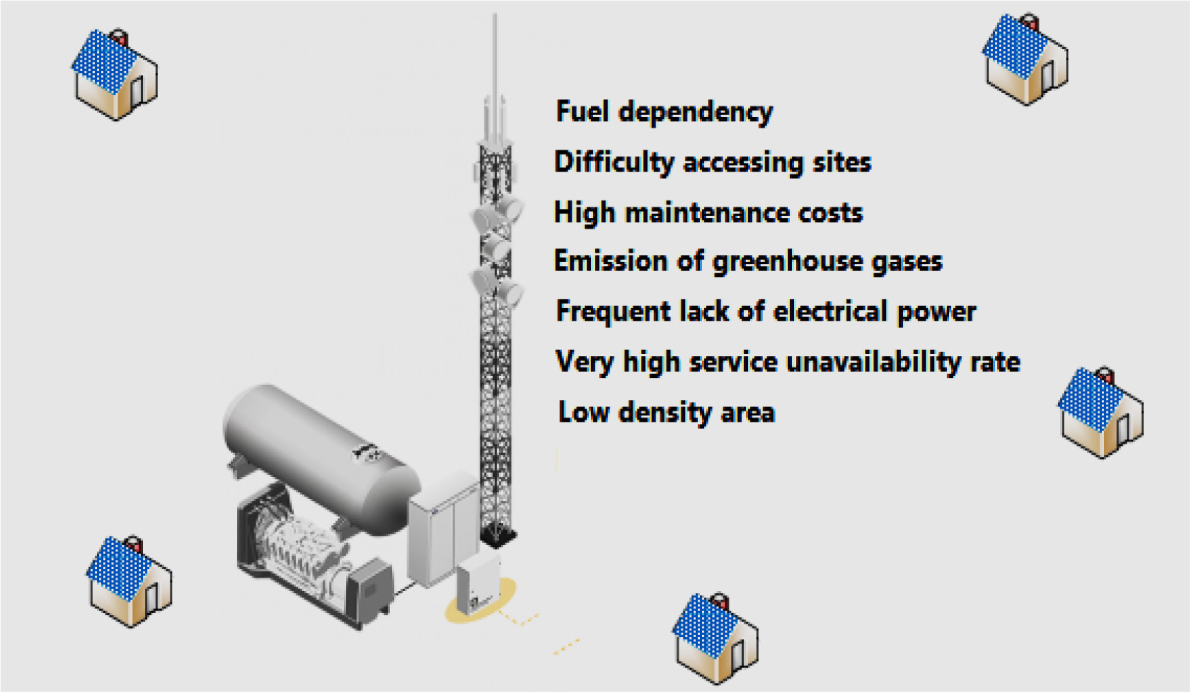
In order to solve the problems often encountered on these sites, namely: frequent service interruptions caused by the lack of energy, high maintenance costs and greenhouse gas emissions, it is proposed to supply operators' sites in rural areas with intelligent microgrids composed of photovoltaic panels as the primary source with which batteries and generators will be associated as shown in Figure 2. In this way, the surplus production can be used to satisfy the needs of the local population such as lighting, handset recharging, etc.
Proposed new energy model for rural operator sites
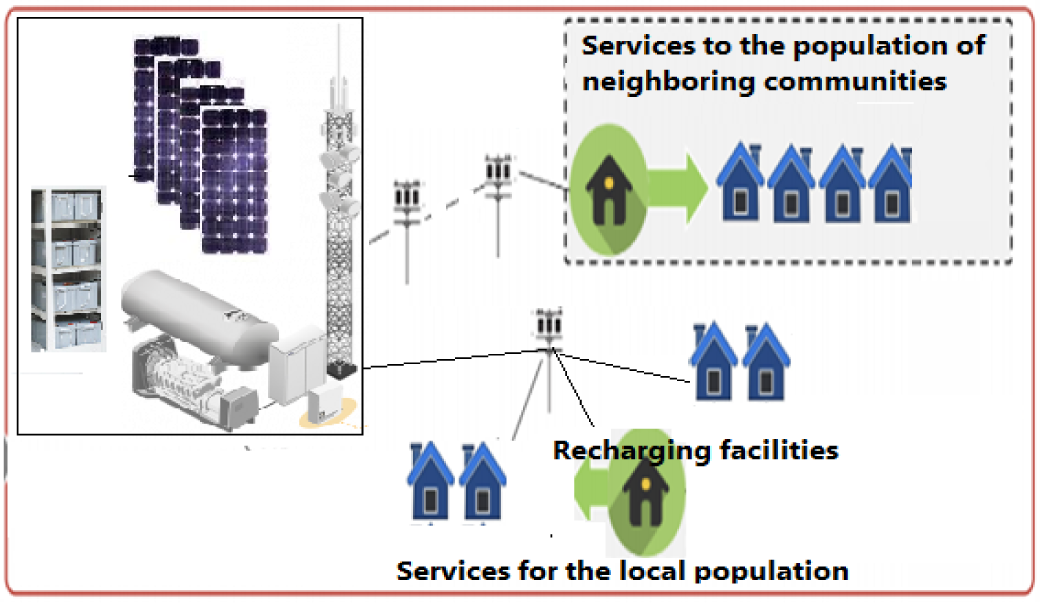
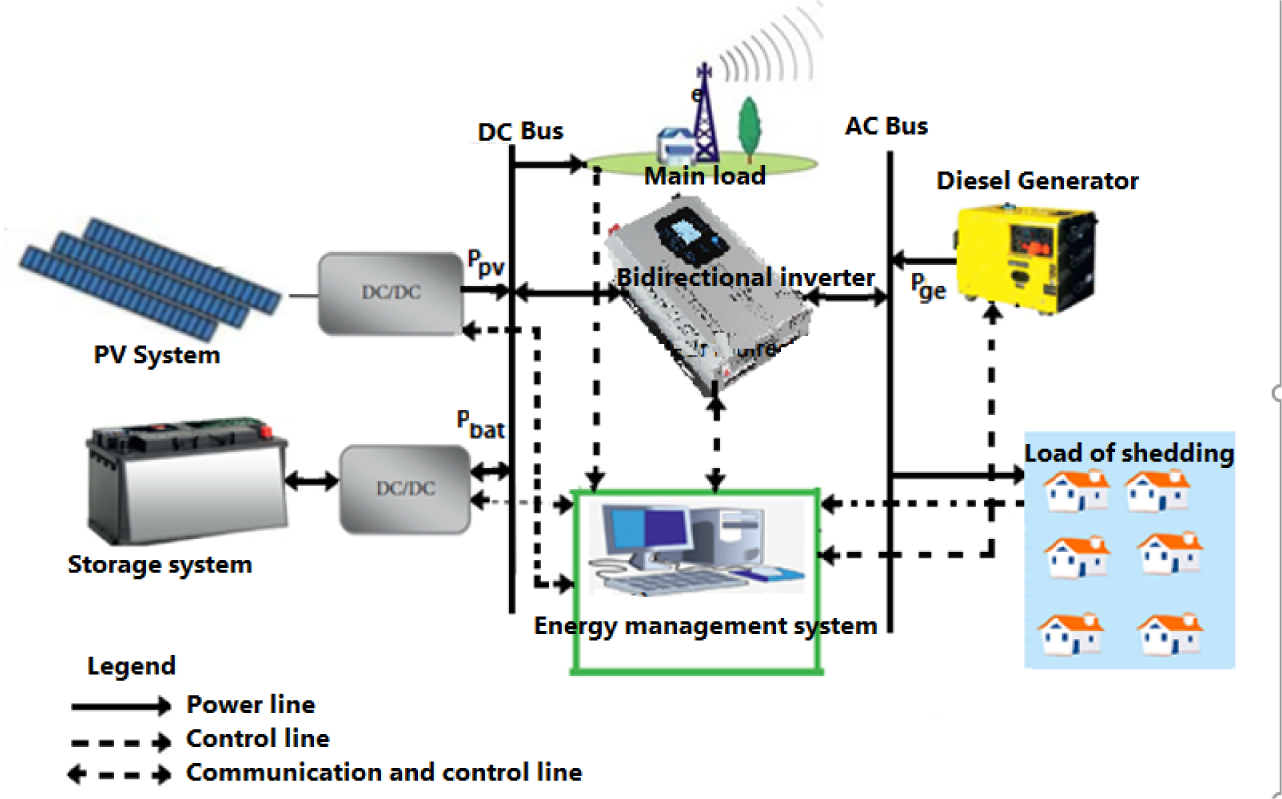
Microgrid is defined as a cluster of interconnected distributed energy resources, energy storage systems, and loads which can operate in parallel with the grid or in an islanded mode. Microgrid can be an DC [35], AC or hybrid AC-DC [36] grids depending on the elements constituting it, such as the sources of production and the loads to be supplied. The classification by scale of microgrids was done by [37]. The system proposed in this study is a hybrid DC-AC microgrid illustrated in Figure 3.
Flow diagram of the hybrid microgrid
Many electrical models of Photovoltaic modules have been developed in the kinds of literatures, such as [38] and [39]. Simplified model that considers the ambient temperature and solar irradiance, expressed by eq. (1) is used in this work.
(1)
where:
- is the output power of PV in watts (W);
- G is the solar radiation in W/m2;
- is the solar radiation at standard test conditions (STC) ( = 1000 W/m2);
- is the rated power in watts (W) at the STC;
- K is the temperature coefficient estimated as -3,7 × 10-3 (1/°C);
- is the ambient temperature in °C ( = 25 °C);
- is the nominal operating temperature of the cell;
- is the cell temperature in °C at STC.
The storage system is modeled as having [40]:
- a total storage capacity measured in MWh;
- a power of storage system, measured in MW;
- a State Of Charge (SOC).
The capacity of the batteries is calculated according to the number of days of autonomy required to satisfy energy demand during periods of unavailability or absence of solar energy. This capacity is estimated by eq. (2):
(2)
where:
- is power of the load;
- DOD is depth of discharge (20%);
- is inverter efficiency (95%);
- is battery efficiency (85%);
- is number of days of autonomy which can be up to 3 or 5 days.
The production of photovoltaic panels is dependent on climatic parameters. It can be either higher than the load requirement or insufficient to satisfy the load requirement. In case of the excess production, is positive and represents power consumed by the storage system [41]. In case of the insufficient production, is negative and represents the additional power that storage system provides to satisfy the load's energy requirement [12]. The battery power is expressed by eq. (3):
(3)
The batteries State Of Charge (SOC) can be determined by the function SOC(t). Its value is between two extreme values: maximum limit and minimum limit . Therefore, the SOC(t) can be expressed by eq. (4) [42].
(4)where:
- γ is the hourly self-discharge rate of battery storage;
- SOC(t) and SOC (t -1) represente the Battery states of charge (Wh) at times t and (t -1) respectivily;
- is inverter efficiency;
- PBat (t) is power of the battery.
It can take three characteristic values, such us: the maximum capacity , the nominal capacity and the minimum capacity , which represents the maximum depth of discharge (DOD). The storage device charges when the following two conditions expressed by eq. (5) are met:
(5)
To guarantee efficient operation and long life of batteries, they must charge and discharge within a given range. This constraint is indicated by eq. (6):
(6)
where:
- is the minimum allowable discharge value for batteries;
- is the maximum charge capacity of batteries.
The diesel generator (DG) is used when the following two conditions are met:
- no or insufficient photovoltaic power generation and;
- storage capacity below the minimum capacity (SOC(t) < ).
The presence of DG in the hybrid system has several advantages, including, reducing the capacity of the storage device and therefore investment cost and increasing the microgrid reliability. The fundamental parameters to be considered for the genset when sizing hybrid systems are [11]:
- Hourly fuel consumption;
- Maximum power it can produce (efficiency);
- Minimum uptime.
The hourly consumption of genset is expressed by the following eq. (7) [43]:
(7)
where:
- is the genset generated (kW);
- Q(t) is the hourly quantity of fuel consumed (L/hour);
- is the nominal power (kW) of the genset;
- a and b are constant parameters (L/kW) representing the fuel consumption coefficients approximated as 0.246 and 0.08415, respectively [44].
To calculate the efficiency of the genset, the following eq. (8) is used [45]:
(8)
where:
- is the genset global efficiency;
- is the genset brake thermal efficiency.
In order to optimize the performance of the genset, it is essential to control the energy it produces. Therefore, eq. (9) is used to restrict the energy produced by DG:
(9)
where:
- is the energy produced by the genset;
- is the genset rate capacity;
- is the genset operating time.
At any time and in any condition, power produced by microgrid must be greater than or equal to site requirement. This constraint is expressed by eq. (10). The sign ("-" or "+") of battery's power depends on fact that battery can discharge or charge:
(10)
where:
- (t) is the main load power at time t;
- is the PV generator power at time t;
- (t) is the storage battery power at time t;
- (t) is the genset power at time t.
Each generator is constrained by a maximum value (t) and a minimum value (t) which can fluctuate from one extreme to the other. This constraint is expressed by eq. (11):
(11)
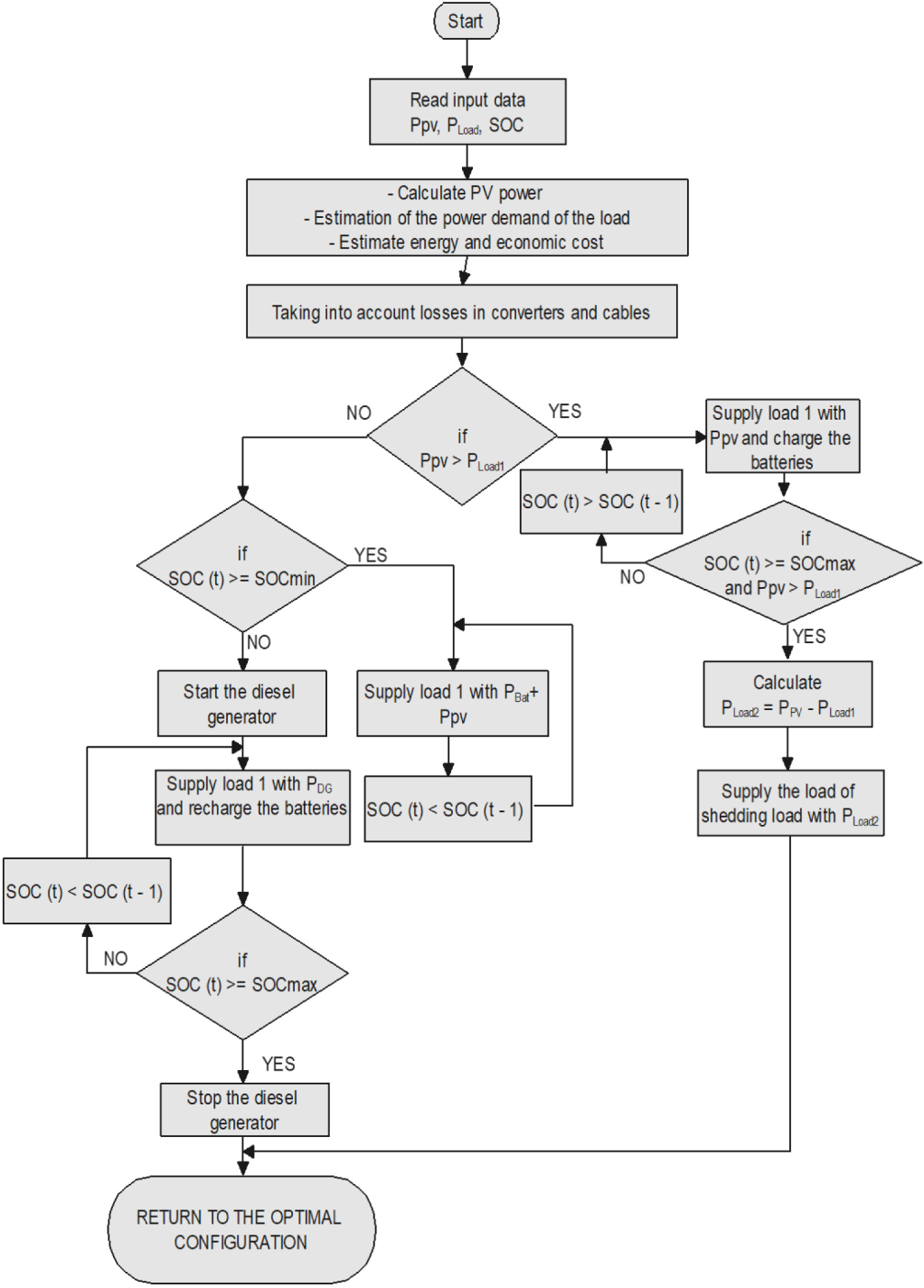
The proposed solution allows to coordinate the energy flow in the microgrid by prioritizing using solar photovoltaic energy systems. The objective is to provide the operators' equipment considered as the main load () and using the excess production to provide electricity to the local population considered as load shedding (). The system operates according to the following conditions:
Condition 1: The PV generator's production exceeds the main load demand , then:
if SOC(t) < , the surplus is used to recharge the storage device;
if SOC(t) = , the surplus is used to supply the shedding load ;
Condition 2: The PV generator's production is less than the main load demand , then:
if , the demand of the main load is satisfied by the contribution of PV production and the batteries energy ;
if , the demand of the main load will be satisfied by the contribution of the generator DG and the energy produced by the solar panels ;
Condition 3: No production of the PV generator , then:
if , the need of the main load will be satisfied by the contribution of the energy stored in the batteries ;
if , then the main load will be provided by the genset only. The surplus production of the genset will be used to charge the batteries . But, as soon as the PV generator production is resumed or , the DG is switched off.
Figure 4 describes the flowchart for intelligent energy management.
The optimization problem addressed in this paper is a nonlinear problem and traditional optimization methods are not suitable for solving this kind of problem. Thus, there is a set of methodologies and computational approaches inspired by nature to treat these complex problems in the real world, such as, artificial neural networks (ANN) [46], fuzzy logic [47], genetic algorithm (GA) [48], Dynamic Programming [49], PSO (Particle Swarm Optimization) algorithm [50], etc. However, none of these methods is considered to be ideal for all situations [51], [52]. Each one of the optimization approaches has its advantages and limitations. Thus, the choice of the best optimization approach depends on the problem to be analyzed to find the solution that maximizes or minimizes a function to be optimized [53]. The algorithm to be used in this study should provide smart and optimal management of microgrids for the smart management of multiple sources in real-time, to always ensure an uninterrupted supply of electric power to the operators' sites, and using the excess generation to provide electricity at a lower cost to the local population. Several authors have made comparative studies of these smart algorithms. For example, according to the authors [54], Particle Swarm Optimization (PSO) is the most widely optimization algorithm for microgrid management used method for microgrid optimization problems because of its robustness, flexibility and fast convergence. The authors [55], [56] and [57] have used it to solve energy management problems involving microgrids.
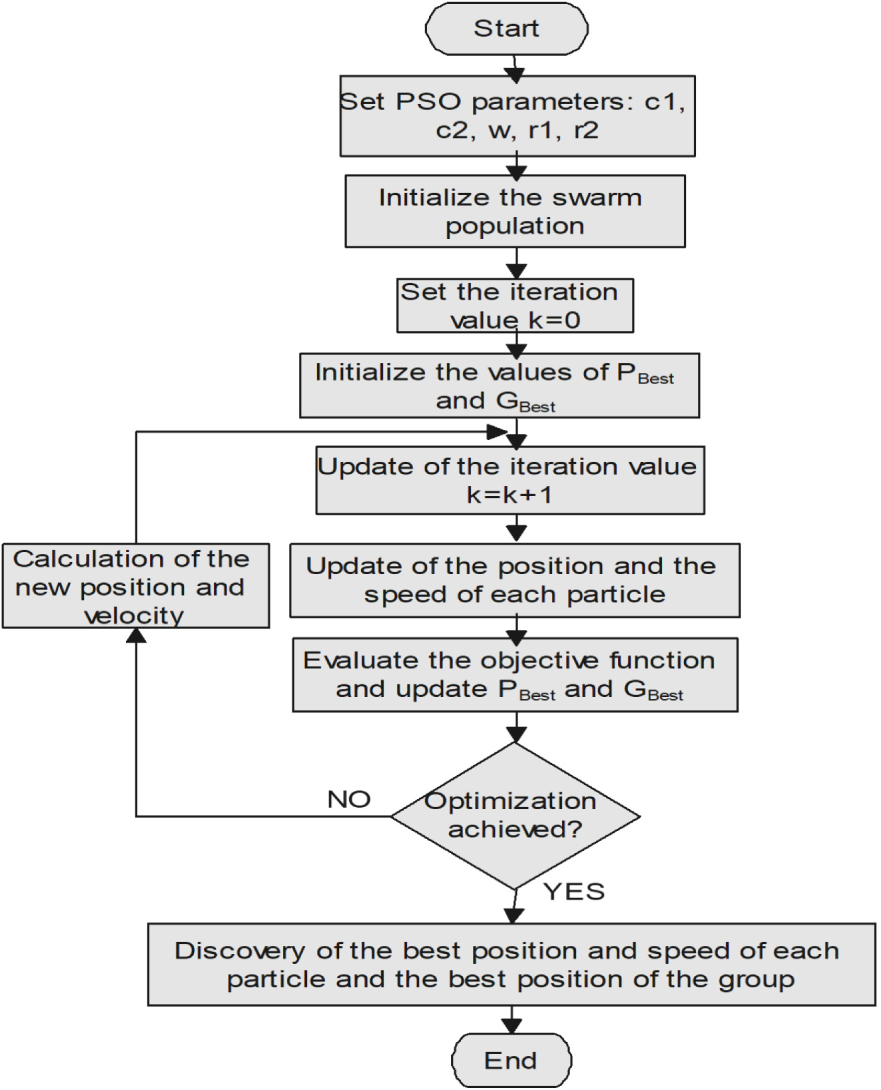
Flowchart for intelligent energy management
Therefore, PSO is chosen in this work to minimize the production and operation cost to ensure the efficient management of energy production and the need. Its practical implementation is done using the PySwarms python package [58].
The PSO algorithm was first proposed in 1995 by Eberhart and Kennedy. It is an optimization method that has been widely used in several fields governed by complex optimization problems. The search strategy of the PSO algorithm is inspired by the social behaviors of bees or birds that act together in a complex way, based on simple "rules", to find a solution to specific optimization problems [59], [60].
In the resolution of optimization problems, two characteristic values are important. The first value, called the best individual value, is the best value recorded solution that each particle has taken up until a given date. This value is called the best individual value. The second, called the global best value, is the best known solution of the whole swarm among the population.
Each particle i in the swarm is characterized, at the given time t, by its position in the search space, that represent the value of the variables and a velocity that directs the particle to the best individual and global values [61]. Thus, the position of each particle in the swarm is updated using the following eq. (12):
(12)
where:
- is the particle position;
- is the velocity of the particle in iteration k.
The velocity of particle i in iteration k is calculated by the following eq. (13):
(13)
where:
- is the best solution of a particle;
- is the best global solution of the swarm;
- k is the number of the current iteration;
- ω is the inertia weight (denotes the coefficient of inertia);
- and are the cognitive and the social confidence coefficient, respectively;
- is coefficient;
- and are random numbers from a uniform distribution on [0, 1] [62].
The fitness function expressed by eq. (14) is a particular type of "objective function" use in this paper to find the optimal possible solutions [12]:
(14)
where:
- F(x) is the vector representing the "objective functions";
- is the individual goals to be achieved;
- x is the vector of the design search space;
- H(x) is the equality constraints;
- G(x) is the inequality constraints.
The indicators that was used as objective functions to arrive at an optimized and reliable system in our study are:
- Economic efficiency indicator (LCOE: Levelized Cost Of Energy) which means the cost of electricity;
- Reliability indicator (LPSP: Loss of Power Supply Probability) which means the probability of loss of generated power;
- Maximum Renewable Factor (MRF), which means the operating time of the DG unit.
In optimizing of hybrid systems, the LCOE (Levelized Cost Of Energy) indicator, estimated by eq. (15), is often used. It expresses the price ($USD/kWh) per unit of energy produced over the system’s lifetime. Low value of LCOE corresponds to a low cost of electricity [63], [64], [65]:
(15)
where:
- TC is the total system cost including the capital, spare parts, the exploitation, and the maintenance costs;
- is the hourly power consumed by the load;
- CRF is the capital recovery factor, expressed by eq. (16).
(16)
where:
- n is the system lifetime, most of the time equal to the lifetime of the PV panels [66];
- β is the economic evaluation discount rate of the proposed system.
To calculate the loss of power supply probability, one often uses the indicator, Loss of Power Supply Probability (LPSP), determined by eq. (17) [64], [67], to evaluate the reliability of the system:
(17)
where:
- is the power produced by the PV generator at time t;
- is the power produced by the genset at time t;
- is the power consumed by the load at time t;
- is the minimum allowable power of the storage system.
The MRF (Maximum Renewable Factor) indicator, expressed by eq. (18), is the utilization rate of the genset. It is used to determine the amount of the energy from the genset compared to the photovoltaic generators. The objective is to minimize the use of GE, reduce CO2 emissions, and reduce exploitation costs. A low utilization rate of the genset involves a reduction in greenhouse gases and operating costs [12]:
(18)
The MRF allows to evaluate the energy produced by the genset compared to the energy produced by the photovoltaic panels. Therefore, MRF = 0, means that the energy produced by the PV generator is zero, MRF = 1, means that energy produced by the genset is zero.
The optimization procedure involves determining the economic parameters of an isolated microgrid for an optimal sizing [68]. These parameters include production, installation and operating costs during the lifetime and payback period of the system. The flowchart of the algorithm applied to the sized system is shown in Figure 5 below.
Flowchart of PSO Algorithm
The following pseudocode describes the main steps of the technical and economic analysis of the dimensioned system.
- Acceleration coefficients, and ;
- Coefficient of inertia ω;
- Number of iteration k;
- Number of iteration n;
Step 1) Initialization phase (Input parameters).
Loading of the annual production data of the dimensioned photovoltaic system.
Loading the annual load characteristics data (load requirements, battery state of charge);
Define the economical parameters of the system;
Define the constants:
Randomly initialize the individual position and the global position ;
Step 2) Set the iteration variable;
Step 3) Set the positions and velocities of each particle in the swarm;
Step 4) Determine the initial value of the objective function;
Step 5) Update the best individual position and global position ;
Step 6) Calculate the parameters LCOE, MRF and LPSP of the objective function;
Step 7) Determination of . The particle with the LCOE and LPSP low, will be considered as the ;
Step 8) Check the stopping Condition. If , stop the algorithm and display the results. If , go to step 2.
Note that in each iteration, the individual targets such us, LPSP, MRF, and LCOE, to be achieved by the generated particles are calculated. In cases they satisfy the constraints, they will be accepted as PSO particles in the population.
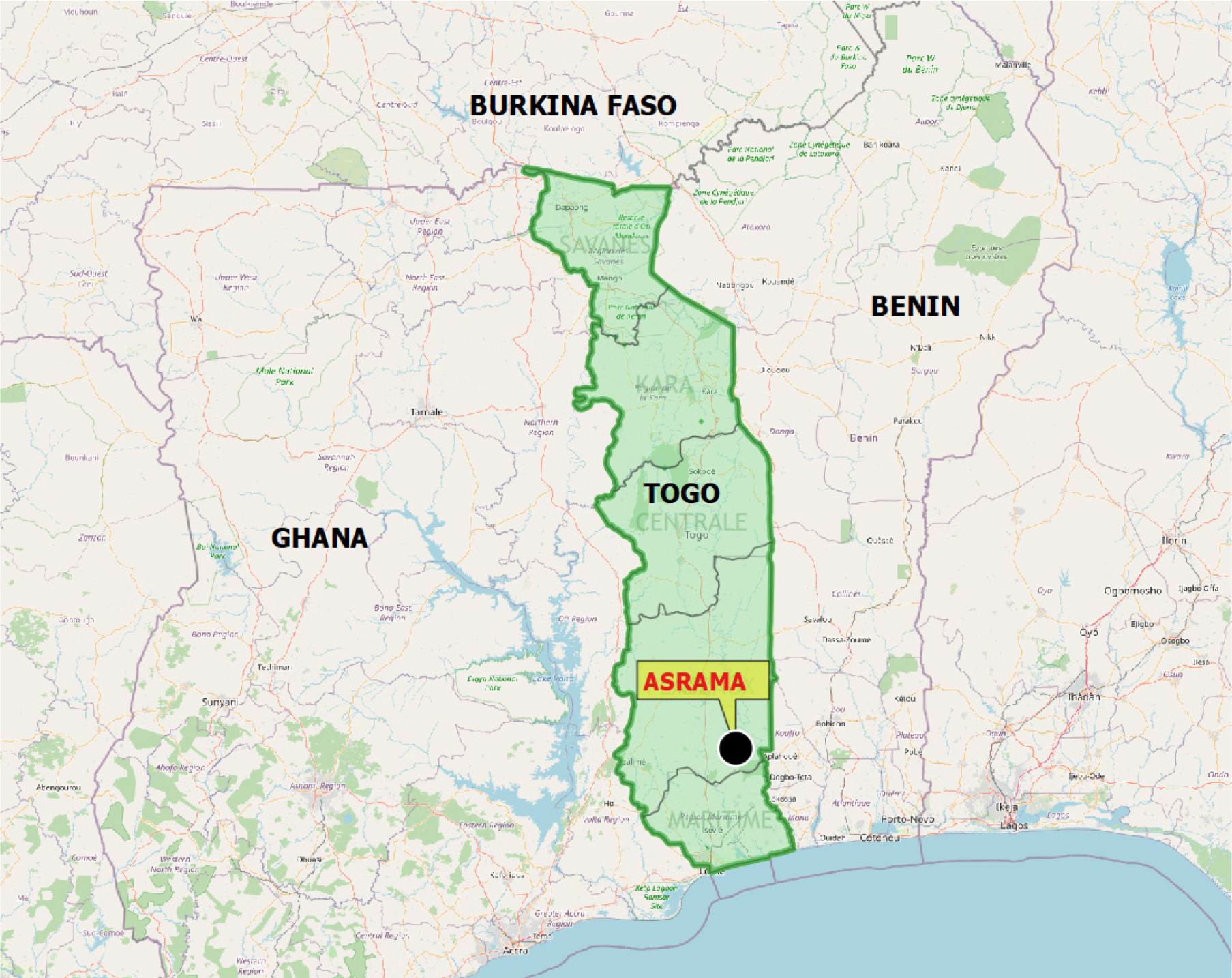
Mobile network operators have set up infrastructures in rural areas to cover these areas with telecommunications networks. These sites are powered by genset, which emit greenhouse gases and generate very high operating costs. One of these sites, which is the subject of this study, is Asrama, located around 120 km from Lomé, capital of Togo. Asrama lies in the Haho prefecture in the Plateaux region of Togo at the Latitude: 7.0023 N, Longitude: 1.4586 E and, altitude: 140 m, as shown in Figure 6.
Geographical location of Asrama
One of the aims of this project is to promote renewable energies, particularly photovoltaics, and to increase the rate of access to electricity in rural areas. To this end, a microgrid has been installed on this site, including solar panels, storage batteries and genset.
The simulations were performed using the PSO algorithm with parameters as inputs: technical and economic data, electrical parameters provided by the microgrid, and the meteorological data on sunshine at a site.
The sizing and installation of microgrid required investments. The technical and economical characteristics of the microgrid installed at the Asrama site are presented in Table 1 below. The initial investment costs were expressed in dollars with 1 $USD = 603.00 FCFA on April 20, 2022.
Technical and economic data on the study electrical system
| System elements | Economic parameters | Values |
|---|---|---|
| Photovoltaic generators | Energy workshop & panels (kWC) | 14.00 |
| Lifetime (years) | 25.00 | |
| Initial cost [$USD/kW] | 212.98 | |
| DC/DC converter efficiency (%) | 95.00 | |
| Genset | Lifetime (hours) | 43,800.00 |
| Initial cost [$USD /kVA] | 67.36 | |
| Power rating (kVA) | 13.00 | |
| Energy storage device | Capacity (Ah) | 2,000.00 |
| Efficiency (%) | 85.00 | |
| Lifetime (years) | 5.00 | |
| Initial cost ($USD /Ah) | 11.30 | |
| Number of days of autonomy | 3.00 | |
| Economic parameters | Operating and maintenance cost (%) | 4.73 |
| Lifetime of the project (years) | 25.00 |
Meteorological data and electrical parameters on the site were measured for 1 year in order to assess the characteristics of the site. These parameters are:
- the annual hourly solar irradiation;
- the energy required for the load;
- the power produced by the PV generator;
- the evolution of the level of charge and discharge of batteries.
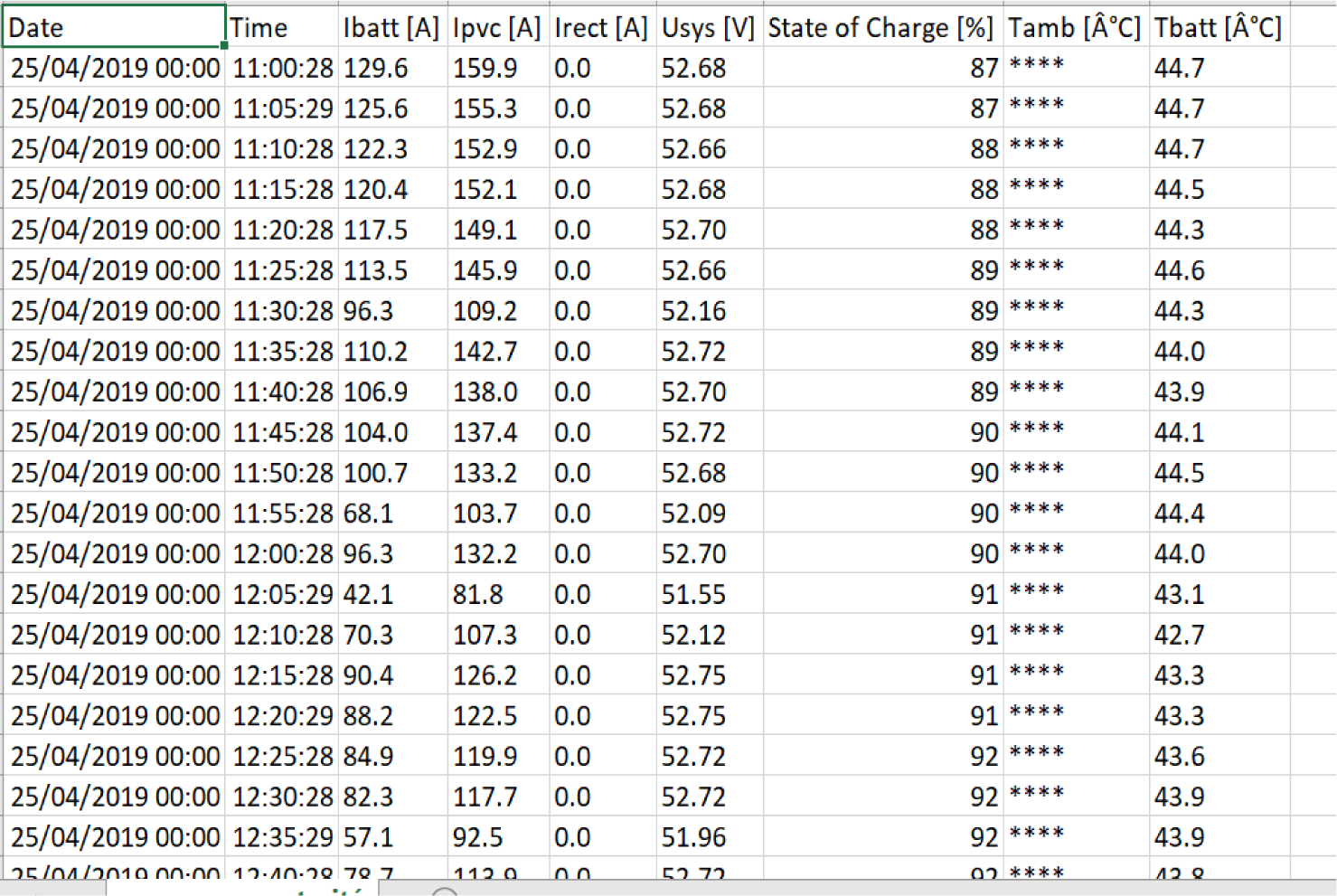
The energy characteristics, such as the energy requirement of the site, the output power of the PV generator, the variation of charge and discharge of the storage device, were measured at the study site for one year. The Figure 7 shows an extract of the measured energy characteristics.
Extract of energy parameters measured at the study site
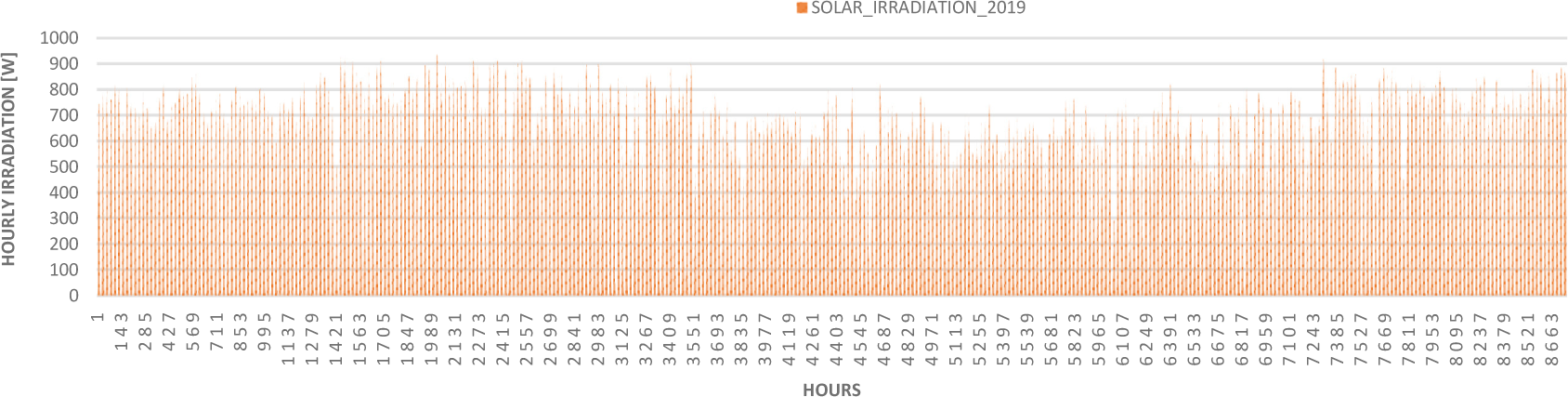
Solar irradiation data are a prerequisite for the sizing of a photovoltaic energy production system. Thus, the hourly solar irradiation for 1 year (January 1 to December 31, 2019, equivalent to 8760 measurements with an hourly step), has been evaluated to assess the solar potential of the study site. Figure 8 illustratesthe solar irradiance potential of the Asrama site [69].
Annual hourly solar irradiation at the Asrama site
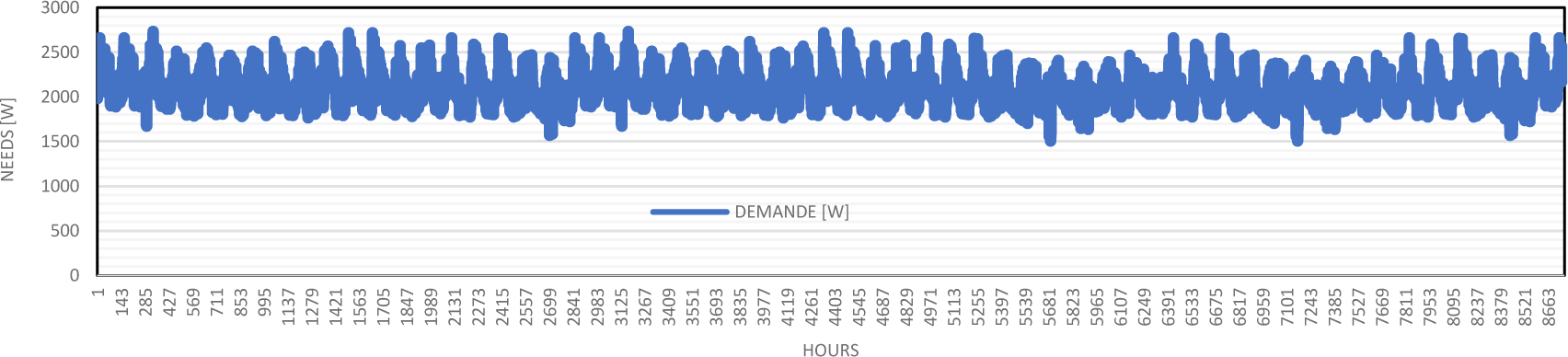
The electrical consumption on the studied site were measured for one year. These data, shown in Figure 9, allowed us to evaluate and assess the consumption needs of the site.
It can be seen in Figure 9 that the consumption needs of the site are almost constant throughout the year and vary between 1.50 kW and 2.73 kW.
Electrical energy requirement of the load
The data of the level of charge and discharge of the batteries were recorded for one year and are shown in Figure 10. It appears in this figure that the genset is not requested during the entire year because the level of charge of the battery varies between 60% and 100%.
Variation of charge and discharge of the battery

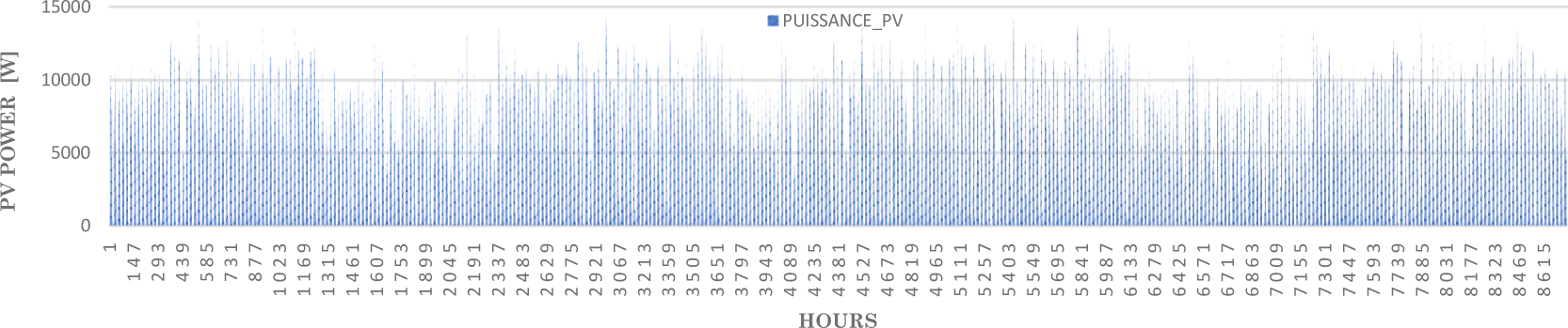
The power produced by the photovoltaic generator, recorded for 1 year at regular intervals, is shown in Figure 11.
Illustration of the power produced by the PV generator
The following section presents the simulation results. The proposed optimization model was simulated with Pyomo software in Python. The solver used in Pyomo was a Gurobi Optimizer v9.5.2 with an academic license. This simulation requires input data, and the simulation parameters.
To achieve a good convergence speed and obtain good expected results, it is important to choose the simulation parameters accordingly. Thus, the simulation parameters chosen in this work are shown in the Table 2 below.
Parameters used in the present work
| Definition | Parameters | Value |
|---|---|---|
| Acceleration coefficients | C1 | 1.495 |
| C2 | 1.495 | |
| Random numbers | r1 | 0.5 |
| r2 | 0.6 | |
| Inertia weight | Ω | 0.729 |
| Number of iteration | K | 100 |
| Number of particles | n | 100 |
To evaluate the performance of the proposed system, the following input data were used:
- the technical and economic data in Table 1;
- the weather data from the site shown in Figure 8;
- the electrical parameters provided by the microgrid, such us, the energy demand of the site shown in Figure 9;
- the output power of the PV generator shown in Figure 11;
- the power of the storage device.
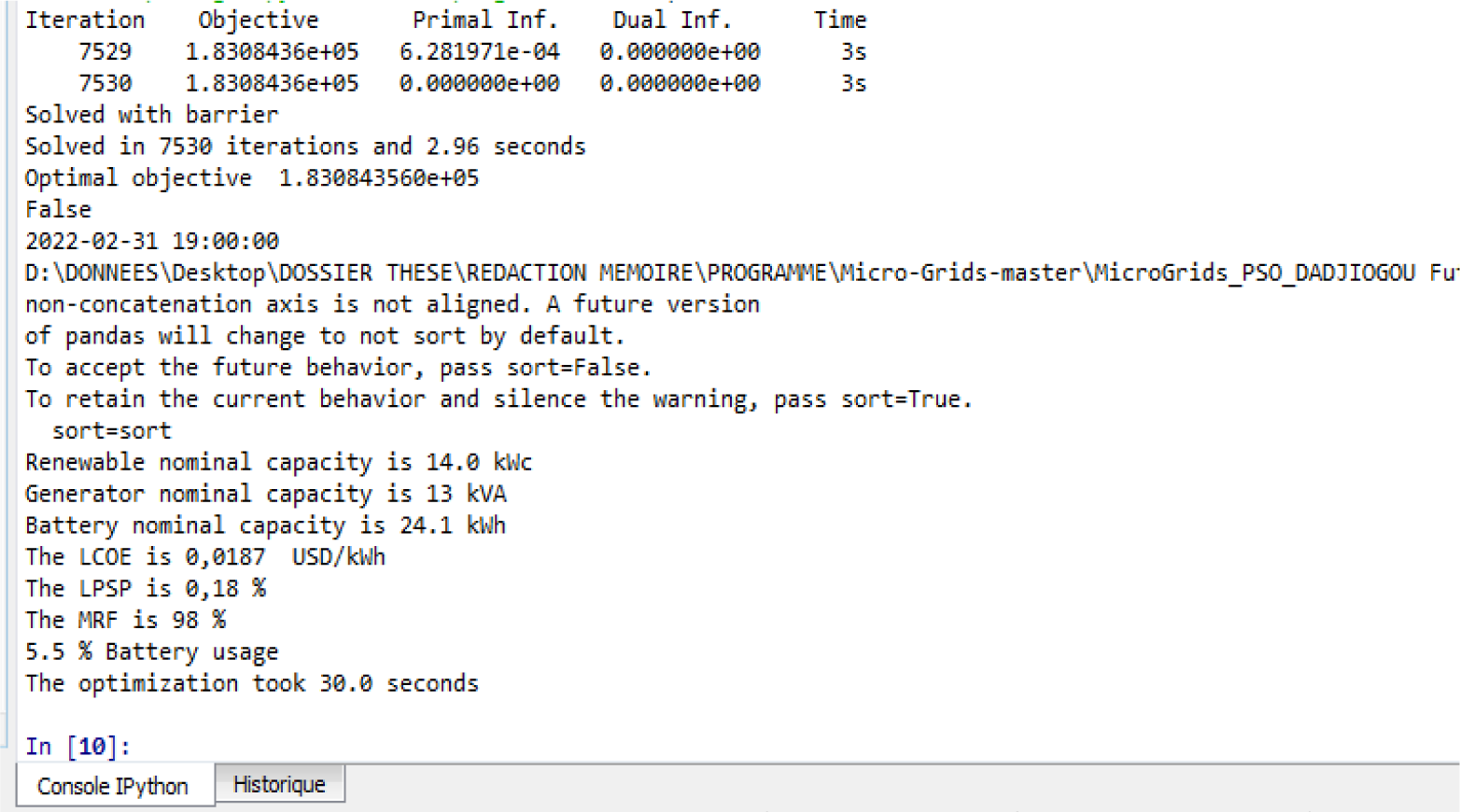
The parameters that were determined are: the cost of electricity generation (LCOE), the probability of loss of power supply (LPSP) and the Maximum Renewable Factor (MRF), which are all the objective functions of the system. Figure 12 shows the results obtained from the simulation of the optimization algorithm in Python.
Results of simulation in Python
The output results are shown in the Table 3 below.
PSO Results
| Parameters | Value | |
|---|---|---|
| Simulation parameters | Number of iterations | 100 |
| Number of particles | 100 | |
| Output Results | LPSP (%) | 0.18 |
| LCOE ($USD/kWh) | 0.0187 | |
| REF (%) | 98 | |
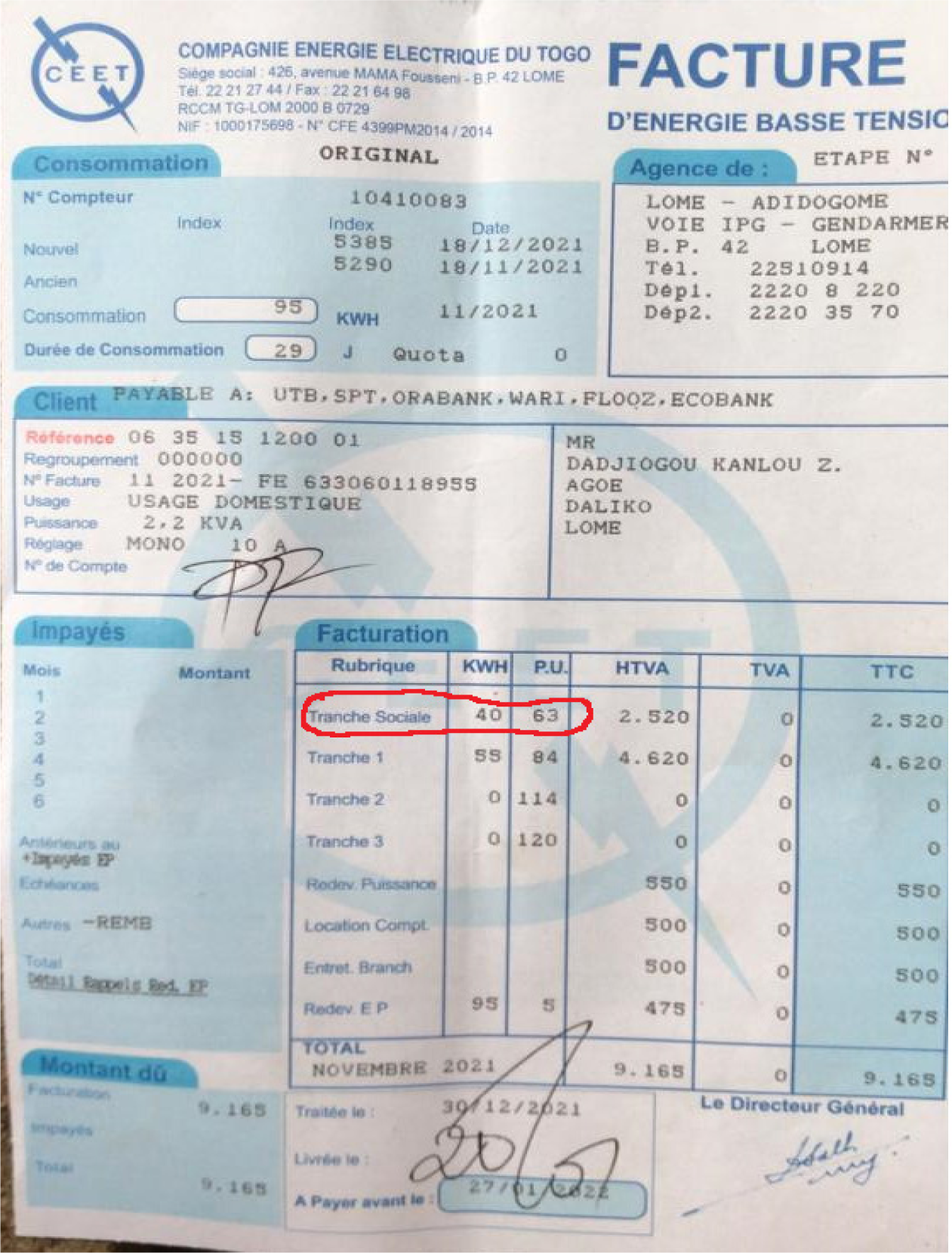
The simulation results obtained show that the system is well optimized with a considerable reduction in the risk of outages, fuel consumption, generator run time and greenhouse gas emissions. Moreover, the overproduction recorded on the operator’s sites can be used to satisfy part of the local population's electrical energy needs. In addition, the solution is very promising and suitable for the low-income population with a low LCOE value equal to US$0.0187 compared to the price charged in urban areas by the national electricity company (CEET) which is US$0.105 for the social class as shown in the following Figure 13.
Bill from the electricity company
A comparative analysis of the three energies, such as, the site requirements, the energy produced by the PV array, and the battery power, is illustrated in Figure 14. A negative battery value (black) indicates that the battery is charging and a positive value indicates that the battery is discharging.
Illustration of energy production and site energy requirements
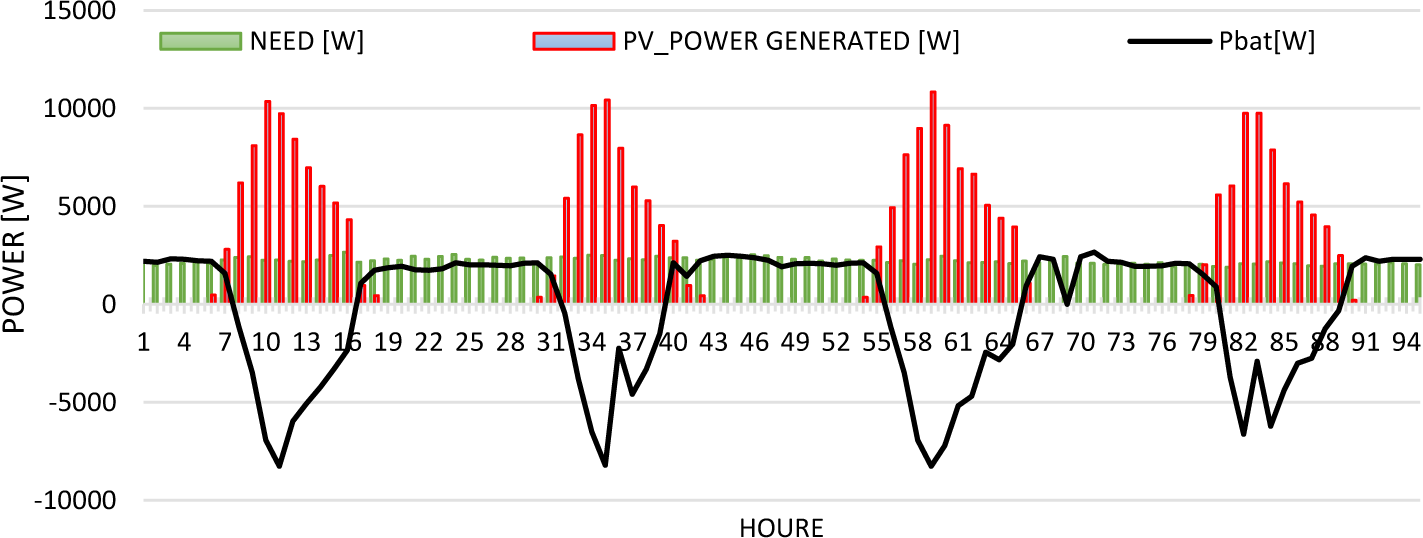
The results of this comparative study show that between 4:00 p.m. and 7:00 a.m., the photovoltaic array production is lower than the site's energy demand. During these times, the site's energy needs are provided by the batteries. During the daytime between 7:00 a.m. and 4:00 p.m., the production of the PV module is greater than the site's energy needs. The excess energy produced by the PV generator is used to recharge the batteries. However, the charge/discharge curve of the batteries shown in Figure 10 indicates that the batteries are underutilized. During the entire year, the genset is rarely used as indicated by the value of MRF=98%.
This work is a contribution to the intelligent management of microgrids that are installed in mobile network operator’s sites in rural areas, in order to achieve the dual objective of universal access to telecommunications and electricity. For this purpose, the PSO (Particle Swarm Optimization) algorithm is used to ensure a real-time intelligent management of the various sources constituting the microgrids and multiple loads to be powered. The uncertain nature of the demand and production of renewable energy is considered to ensure continuity of supply electrical energy to requirement of the main load and to use the excess production to provide electricity at lower cost to the local population.
The simulation of the proposed intelligent energy management scheme using the Asrama site technical and economic parameters allowed the calculation of the evaluation parameters, LPSP, LCOE, and MRF that are defined as objective functions. The low cost of electricity (LCOE) obtained shows that this solution could allow to increase universal access to electrical energy for low-income populations in rural areas. In addition, the MRF value reflects a significant reduction of exploitation costs related to gensets, and greenhouse gas emissions. The energy produced on operator’s sites can be increased according to the demand of the local population.
Operator sites already exist in rural areas in developing countries. Applying this solution to all operator sites, who guarantees a loss of power supply probability (LPSP) value equal to 0.18 % and a cost of electricity (LCOE) value equal to US$ 0.0187, will increase the rate of access to electricity in rural areas, particulary in Sub-Saharan Africa and ensure the convergence of universal access to energy and telecommunications. This convergence will contribute to the development of access to electricity and telecom networks in rural areas through individual or community offers. The synergies between these two sectors will also be a catalyst for investment in broadband telecom infrastructure and power generation capacity.
| a and b | fuel consumption coefficients | [L/KW] |
| C1 | cognitive confidence coefficient | |
| C2 | social confidence coefficient | |
| CB | batteries nominal capacity | [Ah] |
| CDG | rate capacity of the DG | |
| CRF | capital recovery factor | |
| EDG | energy produced by the DG | [kWh] |
| DOD | depth of discharge | |
| fi(x) | individual goals to be achieved | |
| F(x) | vector representing the "objective functions" | |
| G | solar radiation | [W/m2] |
| G(x) | set of equality constraints | |
| Gbest | best global position | |
| Gref | solar radiation at standard test conditions (STC) | [W/m2] |
| H(x) | set of inequality constraints | |
| k | number of the current iteration | |
| K | temperature coefficient | [°C] |
| LCOE | Levelized Cost of Electricity | [$USD/kWh] |
| LPSP | Power Supply Probability | [%] |
| MRF | Maximum Renewable Factor | [%] |
| n | system lifetime, often equal to the lifetime of the PV panels | [years] |
| NDA | number of days of autonomy | [day] |
| PDG | power of the generator DG | [kWh] |
| PDmin(t) | minimum allowable discharge value for batteries | [kWh] |
| PBat | power of the storage battery | [kWh] |
| PBatmin | minimum allowable power of the storage system | [kWh] |
| Pbest | best position of the individual particle | [kWh] |
| PCmax(t) | maximum charge capacity of batteries | [kWh] |
| PLoad | amount of energy consumed per hour | [kWh] |
| PLoad1 | power of the main load | [kWh] |
| Pmax | maximum value of power | [kWh] |
| Pmin | minimum value of power | [kWh] |
| PPV | output power of PV | [kWh] |
| Pr | rated power of the DG | [kWh] |
| Q | fuel consumption | [L/hour] |
| r1 and r2 | random numbers from a uniform distribution | |
| SOC | battery states of charge | [Ah] |
| SOSmax | maximum capacity | [Ah] |
| SOSmin | minimum capacity | [Ah] |
| Tamb | ambient temperature | [°C] |
| TC | total system cost of the whole system including the capital, spare parts, the exploitation, and the maintenance costs | [$USD] |
| TNOCT | nominal operating temperature of the cel | [°C] |
| Tref | cell temperature | [°C] |
| X | vector of the design search space | |
| xi | position of the particle | |
| Vi | velocity of the particle in iteration | [m/s] |
| β | discount rate used in the economic evaluation of the proposed system |
| ηInv | inverter efficiency |
| ηBat | battery efficiency |
| ηg | overall efficiency of diesel generator |
| ηTF | thermal efficiency of the brake of DG |
| γ | hourly self-discharge rate of battery storage |
| ∆t | operating time of the DG |
| ω | coefficient of inertia |
| AC | Alternating Current |
| ANN | Artificial Neural Networks |
| DC | Direct Current |
| DE | Differential Evolution |
| EMS | Energy Management Systems |
| GA | Genetic Algorithm |
| GWO | Grey Wolf Optimizer |
| IoT | Internet of Things |
| LFR | Loss-Free Resistor |
| NDP | National Development Plan |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| SDGs | Sustainable Development Goals |
The authors would like to express their gratitude to ENSI for its technical support and to the University of Lome for allowing access to its laboratory facilities. The authors are grateful to the LARSI laboratory in which this research was done and the CERME for its financial support. Sincere thanks to Dr. Widi TCHALA for his availability and his constructive criticisms which helped to improve the clarity of this document.
Special appreciation is also credited to all the reviewers for their valuable comments and those who contributed to the realization of this work.
- , Électricité et télécom en Afrique: la convergence?, 2017
- ,
Electricity Access in Sub-Saharan Africa ,Washington, DC 20433: Africa Development Forum Series , 2019, https://doi.org/https://doi.org/10.1596/978-1-4648-1361-0_ch1 - Plan National De Developpement (PND), 2018, https://www.togofirst.com/media/attachments/2019/04/02/-pnd-2018-2022.pdf
- ,
Decentralized Energy Management System in Microgrid Considering Uncertainty and Demand Response ,Electron , Vol. 12 (1),pp 1-19 , 2023, https://doi.org/https://doi.org/10.3390/electronics12010237 - , Energy management system of a microgrid with distributed generation, M.Sc. Thesis, University of Ontario Institute of Technology, 2019
- ,
Energy Management Model for a Standalone Hybrid Microgrid through a Particle Swarm Optimization and Artificial Neural Networks Approach ,Energy Convers. Manag. , Vol. 267 ,pp 115920 , 2022, https://doi.org/https://doi.org/10.1016/j.enconman.2022.115920 - ,
Techno-Economic Analysis and Optimisation of Campus Grid-Connected Hybrid Renewable Energy System Using HOMER Grid , 2022, https://doi.org/https://doi.org/10.3390/su14137735 - ,
Simulation of Solar Off-Grid Photovoltaic System for Residential Unit ,Int. J. Sustain. Green Energy. Spec. Issue Eng. Solut. High Perform. Sol. Energy Syst. , Vol. 4 (1),pp 29-33 , 2014 - , Design and simulation of an independent solar home system with battery backup, 4th Int. Conf. Adv. Electr. Eng. ICAEE 2017, 2017
- ,
Size optimization based on design of experiments of a water desalination process supplied by hybrid PV / Wind system with battery storage , (Sge),pp 3-5 , 2018 - , Design and realization of smart energy management system for Standalone PV system, IOP Conference Series: Earth and Environmental Science, 2022
- ,
Multiobjective Sizing of an Autonomous Hybrid Microgrid Using a Multimodal Delayed PSO Algorithm: A Case Study of a Fishing Village ,Comput. Intell. Neurosci. , Vol. 2020 , 2020, https://doi.org/https://doi.org/10.1155/2020/8894094 - ,
Standalone photovoltaic systems sizing optimization using design space approach: Case study for residential lighting load , 2015 - ,
Optimizing PV Microgrid Isolated Electrification Projects-A Case Study in Ecuador ,Mathematics , Vol. 10 (8), 2022, https://doi.org/https://doi.org/10.3390/math10081226 - ,
Techno ‑ economic analysis of PV systems installed by using innovative strategies for smart sustainable agriculture farms ,Environ. Dev. Sustain. , (0123456789), 2023, https://doi.org/https://doi.org/10.1007/s10668-023-02919-5 - ,
Robust Optimal Utilization in a Grid-Interfaced PV System Using an Efficient Controller with a GWO Control Strategy ,pp 4 , 2022, https://doi.org/https://doi.org/10.3390/materproc2022010004 - ,
A stand-alone Photovoltaic System Design and Sizing: a Greenhouse Application in Sabha City : Case study in Libya A 013 A stand-alone Photovoltaic System Design and Sizing : a Greenhouse Application in Sabha City : Case study in Libya , Vol. 7480 , 2016 - ,
Design & Sizing of Stand-alone Solar Power Systems A house Iraq ,Recent Adv. Renew. Energy Sources ,pp 145-150 , 2013 - ,
An analysis of hybrid power generation systems for a residential load , Vol. 20 , 2017, https://doi.org/https://doi.org/10.1051/e3sconf/20171401020 - ,
A techno-economic analysis of off-grid solar PV system: A case study for Punjab Province in Pakistan ,Processes , Vol. 7 (10),pp 1-14 , 2019, https://doi.org/https://doi.org/10.3390/pr7100708 - ,
Optimization with a simulated annealing algorithm of a hybrid system for renewable energy including battery and hydrogen storage ,Energy , Vol. 163 ,pp 191-207 , 2018, https://doi.org/https://doi.org/10.1016/j.energy.2018.08.112 - ,
Feasibility Study for Off-Grid Hybrid Power Systems Considering an Energy Efficiency Initiative for an Island in Ecuador ,Energies , Vol. 15 (5), 2022, https://doi.org/https://doi.org/10.3390/en15051776 - , Off-grid photovoltaic systems as a solution for the ambient pollution avoidance and Iraq's rural areas electrification, E3S Web Conf., 2016
- ,
A Comprehensive Review on Techno-Economic Analysis and Optimal Sizing of Hybrid Renewable Energy Sources with Energy Storage Systems ,Energies , Vol. 16 (2), 2023, https://doi.org/https://doi.org/10.3390/en16020642 - ,
Methodology for optimal sizing of stand-alone photovoltaic/wind-generator systems using genetic algorithms ,Sol. Energy , Vol. 80 (9),pp 1072-1088 , 2006, https://doi.org/https://doi.org/10.1016/j.solener.2005.11.002 - ,
Assessment of Stand-Alone Photovoltaic System and Mini-Grid Solar System as Solutions to Electrification of Remote Villages in Afghanistan , Vol. 4 (2),pp 92-99 , 2021, https://doi.org/https://doi.org/10.53894/ijirss.v4i2.62 - , Design of a standalone PV system for the all-weather condition: A practical approach, AIP Conf. Proc., 2022
- ,
Multi-Objective Optimal Dispatching and Operation Control of a Grid Connected Microgrid Considering Power Loss of Conversion Devices ,J. Sustain. Dev. Energy, Water Environ. Syst. , Vol. 10 (3), 2022, https://doi.org/https://doi.org/10.13044/j.sdewes.d9.0404 - ,
Isolated Microgrid Design with High Renewable Energy Penetration with a Reliability Objective ,Docteur de l'Université de la Reunion , 2022 - ,
A cross-european analysis of the impact of electricity pricing on battery uptake in residential microgrids with photovoltaic units ,J. Sustain. Dev. Energy, Water Environ. Syst. , Vol. 9 (3), 2021, https://doi.org/https://doi.org/10.13044/j.sdewes.d8.0368 - ,
Modelling and Control of Modular DC-Nanogrids Based on Loss-Free Resistors ,IEEE Access , Vol. 8 ,pp 33305-33317 , 2020, https://doi.org/https://doi.org/10.1109/ACCESS.2020.2974036 - ,
Optimal Design of a Hybrid Off-Grid Renewable Energy System Using Techno-Economic and Sensitivity Analysis for a Rural Remote Location , 2022, https://doi.org/https://doi.org/10.3390/su142215393 - ,
Energy management and optimization of a PV/diesel/battery hybrid energy system using a combined dispatch strategy ,Sustain. , Vol. 11 (3), 2019, https://doi.org/https://doi.org/10.3390/su11030683 - ,
Solar photovoltaic (PV ) applications in Libya : Challenges , potential , opportunities and future perspectives ,Clean. Eng. Technol. , Vol. 5 ,pp 100267 , 2021, https://doi.org/https://doi.org/10.1016/j.clet.2021.100267 - ,
Modeling and control of a solar-thermal dish-stirling coupled PMDC generator and battery based DC microgrid in the framework of the ENERGY NEXUS ,Energy Nexus , Vol. 5 ,pp 100048 , 2022, https://doi.org/https://doi.org/10.1016/j.nexus.2022.100048 - ,
Hybrid AC/DC microgrid test system simulation: grid-connected mode ,Heliyon , Vol. 5 (12), 2019, https://doi.org/https://doi.org/10.1016/j.heliyon.2019.e02862 - , A brief review on microgrids: Operation, applications, modeling, and control, International Transactions on Electrical Energy Systems
- , Microgrid modeling approaches for information and energy fluxes management based on PSO, ICINCO 2019 - Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics, 2019
- ,
An Improved PSO Algorithm for Smooth Path Planning of Mobile Robots using Continuous High-Degree Bezier Curve , 2021, https://doi.org/https://doi.org/10.1016/j.asoc.2020.106960 - ,
Battery Energy Storage System Models for Microgrid Stability Analysis and Dynamic Simulation , 2017, https://doi.org/https://doi.org/10.1109/TPWRS.2017.2740163 - ,
www.etasr.com Dhaked et al.: Battery Charging Optimization of Solar Energy based Telecom Sites in India , 2019, https://doi.org/https://doi.org/10.48084/etasr.3121 - ,
Battery State of Charge calculation with EPC Converters ,Appl. Note - AN026 , Vol. 5 , 2020 - ,
Hybrid Diesel/PV Multi-Megawatt Plant Seasonal Behavioral Model to Analyze Microgrid Effectiveness: Case Study of a Mining Site Electrification ,Processes , Vol. 10 (11),pp 2164 , 2022, https://doi.org/https://doi.org/10.3390/pr10112164 - ,
Techno-economic optimization of small-scale hybrid energy systems using manta ray foraging optimizer ,Electron. , Vol. 9 (12),pp 1-23 , 2020, https://doi.org/https://doi.org/10.3390/electronics9122045 - ,
Sustainable electricity generation for rural and peri-urban populations of sub-Saharan Africa: The "flexy-energy" concept ,Energy Policy , Vol. 39 (1),pp 131-141 , 2011, https://doi.org/https://doi.org/10.1016/j.enpol.2010.09.021 - ,
Energy Management Method of Hybrid AC / DC Microgrid Using Artificial Neural Network , 2021, https://doi.org/https://doi.org/10.3390/electronics10161939 - ,
A Fuzzy-Logic Based Control Methodology for Secure Operation of a Microgrid in Interconnected and Isolated Modes ,pp 1-17 , 2017, https://doi.org/https://doi.org/10.1002/etep.2389 - ,
Voltage Regulation in an Islanded Microgrid using a GA- based Optimization Technique , Vol. 70 (4),pp 15-20 , 2022, https://doi.org/https://doi.org/10.14445/22315381/IJETT-V70I4P202 - ,
Iterative Dynamic Programming - An Efficient Method for the Validation of Power Flow Control Strategies ,pp 542-562 , 2022, https://doi.org/https://doi.org/10.3390/electricity3040027 - , PSO Algorithm for an Optimal Power Controller in a Microgrid, IOP Conference Series: Earth and Environmental Science, 2017
- ,
A survey on computational intelligence applications in distribution network optimization ,Electronics (Switzerland) , Vol. 10 (11), , https://doi.org/https://doi.org/10.3390/electronics10111247 - ,
Particle Swarm Optimization: A Comprehensive Survey ,IEEE Access , Vol. 10 ,pp 10031-10061 , 2022, https://doi.org/https://doi.org/10.1109/ACCESS.2022.3142859 - ,
Smart energy management system for optimal microgrid economic operation , Vol. 5 ,pp 258-267 , 2011, https://doi.org/https://doi.org/10.1049/iet-rpg.2010.0052 - ,
A comprehensive review of planning, modeling, optimization, and control of distributed energy systems ,Carbon Neutrality , Vol. 1 (1), 2022, https://doi.org/https://doi.org/10.1007/s43979-022-00029-1 - ,
Power Dispatching of Multi-Microgrid Based on Improved CS Aiming at Economic Optimization on Source-Network-Load-Storage ,Electron. , Vol. 11 (17), 2022, https://doi.org/https://doi.org/10.3390/electronics11172742 - ,
Optimization Algorithms in Smart Grids: A Systematic Literature Review ,pp 1-19 , 2023 - ,
Particle swarm optimization for micro-grid power management and load scheduling ,Int. J. Energy Econ. Policy , Vol. 10 (2),pp 71-80 , 2020, https://doi.org/https://doi.org/10.32479/ijeep.8568 - ,
Swarm Intelligence: Coding and Visualising Particle Swarm Optimisation in Python , 2022 - ,
A novel framework-based cuckoo search algorithm for sizing and optimization of grid-independent hybrid renewable energy systems ,Int. J. Green Energy , Vol. 16 (1),pp 86-100 , 2019, https://doi.org/https://doi.org/10.1080/15435075.2018.1533837 - ,
PSO-Based Model Predictive Control for Load Frequency Regulation with Wind Turbines ,Energies , Vol. 15 (21),pp 8219 , 2022, https://doi.org/https://doi.org/10.3390/en15218219 - ,
An Overview of Variants and Advancements of PSO Algorithm ,Applied Sciences (Switzerland) , Vol. 12 (17), , https://doi.org/https://doi.org/10.3390/app12178392 - ,
An Improved PSO Algorithm for Smooth Path Planning of Mobile Robots using Continuous High-Degree Bezier Curve , 2020, https://doi.org/https://doi.org/10.1016/j.asoc.2020.106960 - ,
Optimal Configuration for Design of Stand-Alone PV System ,Smart Grid Renew. Energy , Vol. 03 (02),pp 139-147 , 2012, https://doi.org/https://doi.org/10.4236/sgre.2012.32020 - ,
Optimal Design of Hybrid Renewable Energy Systems Considering Weather Forecasting Using Recurrent Neural Networks ,Energies , Vol. 15 (23), 2022, https://doi.org/https://doi.org/10.3390/en15239045 - ,
Review on the cost optimization of microgrids via particle swarm optimization ,Int. J. Energy Environ. Eng. , Vol. 11 (1),pp 73-89 , 2020, https://doi.org/https://doi.org/10.1007/s40095-019-00332-1 - ,
Sizing and Design of a PV-Wind-Fuel Cell Storage System Integrated into a Grid Considering the Uncertainty of Load Demand Using the Marine Predators Algorithm ,Mathematics , Vol. 10 (19), 2022, https://doi.org/https://doi.org/10.3390/math10193708 - ,
Multi-Objective Hybrid Optimization for Optimal Sizing of a Hybrid Renewable Power System for Home Applications ,Energies , Vol. 16 (1), 2023, https://doi.org/https://doi.org/10.3390/en16010096 - ,
Energy management system in microgrids: A comprehensive review ,Sustain. , Vol. 13 (19),pp 1-33 , 2021, https://doi.org/https://doi.org/10.3390/su131910492 - ,
Analysis of the Solar Potential and Realization of the Atlas of the Solar Irradiation of Togo for the Production of Photovoltaic Energy ,J. Eng. Sci. Technol. Rev. , Vol. 15 (5),pp 140-144 , 2022, https://doi.org/https://doi.org/10.25103/jestr.155.18




