Transient regimes correspond to a fraction of a gas turbine life. However, it is known that during changes in the turbine operating conditions (e.g., start-up, load change, shut-down) instabilities and violations of operating constraints may occur, which not only reduce the equipment useful life, but can also lead to total damage and, in extreme cases, to explosions [1]. In this context, this work presents a comprehensive gas turbine control strategy as a means to avoid unsafe or inappropriate operation.
The most important limitations related to gas turbine operation are associated with the compressor and the turbine. Regarding the compressor, main concerns are related to the surge onset, characterized by airflow instabilities associated with a pressure drop in the discharge. Concerning the turbine, metallurgical issues must be considered with regard to the inlet temperature. Outlet temperature may also be limited when a gas turbine is used in a combined cycle, in order to achieve adequate steam quality level. Another restriction that may be considered is related to the environmental impact, where emission reductions may be achieved using combustion controls. Besides operational constraints, there are constructive limitations. For instance, valves cannot provide more clearance than their constructive limit. Moreover, actuators can only open or close with a speed limitation. Thus, it is only possible to manipulate fuel flow gradually.
Process control is the tool to address solutions to safety, environmental, or constructive constraints. Although Proportional-Integral-Derivative (PID) control strategy is routinely applied to gas turbines, such approach does not explicitly cope with all the aforementioned constraints. The present work aims to examine the application of a nonlinear Model-based Predictive Control (MPC) to a gas turbine. The proposed methodology advantageously includes constraints in the optimization procedure explicitly, and, therefore, guarantees that variables will not exceed their limits [2].
Additionally, the optimization algorithm may consider not only the controlled variables, but also include further goals. Concerning a sustainable approach, the model-based predictive control can cope with objectives such as the minimization of greenhouse emissions or the reduction of fuel consumption, for instance.
Model predictive control is widely used in energy systems control, such as photovoltaic system [3], building energy [4], regenerative braking system [5] and interconnected power systems [6]. However, in the literature, works on gas turbine control are mostly focused on PID. In general, those studies that deal with the application of MPC to gas turbines make use of simplified mathematical linear models. Applications of MPC with nonlinear first principle models are found in chemical processes controls in refineries [7]. The representation of the nonlinear dynamics of a gas turbine in the present strategy is accomplished through the DESTUR program, a comprehensive first principle computational modeling tool [8].
Thus, although there are several works on modeling and control of gas turbines, the nonlinear models are obtained from identification techniques of a gas turbine around a specific operating point. Such technique is suitable for turbines operating in close range of operation. The novelty of the present work is the use of a nonlinear model that represents a wide range of operation, appropriate for modelling and control a situation such as load rejection.
In this work, MPC is implemented in the MATLAB® software, integrated with the DESTUR process simulator. The control process relies on an optimization problem, where the objective function to be minimized is the error between the predicted output of the system and the desired value during a certain future period (control horizon). The minimization technique employed is the differential evolution algorithm [9], implemented as in Pires et al. [10]. Results are obtained for three simulated cases of the gas turbine control problem: fuel consumption reduction, load removal/addition and load rejection.
Research on MPC applications to gas turbine control starts in 1997 [2]. Nevertheless, there have been few publications directly related to the subject. Linear models are usually employed to represent the gas turbines. In addition, few works seem to investigate the possibility of hierarchical model predictive control to gas turbines, where the action of decentralized controllers is coordinated by an algorithm operating at a higher level. A most comprehensive work on the application of MPC to gas turbines is presented by Viassolo et al. [11], which shows the advances from the pioneering ideas of Vroemen et al. [12] and van Essen [13], by dealing with noise measurement, and considering fuel consumption minimization in an MPC strategy.
The origins of turbine simulation trace back to the 1950s, when Gold and Rosenzweig [14] developed a method to estimate the gas turbine response speed. Since then, many computational models for turbine performance analysis have emerged, such as HYDES, NEPOMP, NNEP, TURBOMATCH and DYNGEN, TURBOTRANS, GTRANS, DEAN, COTRAN [15]. During the 1980s Rowen [16] proposed a simplified mathematical model to represent a heavy-duty single-shaft gas turbine, which became the most cited work in the field. Later, the author presented an improvement of his first model, considering the Variable Inlet Guide Vanes (VIGV) [17].
In the following years, several works in the field were published proposing different methodologies to construct linear and nonlinear models, such as identification techniques described in the work of Pozzani [18] and those assessed by Yee et al. [19]. More recently, many gas turbine models were developed aiming to assess different control strategies, such as the transient simulator DESTUR, which was applied to assess different PID control strategies by Avellar et al. [20], Avellar [21] and Assumpção [22].
Ultimately, a control strategy for the operation of a gas turbine is important during transient modes that may occur during startup, shutdown, and perturbations, such as load changes in power generation applications or disturbance in fuel injection in aircraft applications. The objective is to respond to those perturbations while keeping the operation out of instability regions (e.g., surge) and without exceeding design limits (e.g., turbine inlet temperature). Typically, the inlet fuel flow rate in the combustion chamber and the air flow rate in the compressor are manipulated, while inlet temperature, compressor stability region, fuel-air ratio in the combustion chamber and shaft speed are monitored.
Boyce [23] states that all gas turbines are manufactured with native control systems. One of the most common control methodologies is the logic proposed by Rowen, which considers speed, acceleration, temperature, as well as upper and lower limits for the fuel mass flow rate as the main controls. The strategy involves one PID loop for the fuel flow, and another PID loop for positioning VIGV.
Vroemen et al. [12] and van Essen [13] were the first to apply model-based predictive control to a gas turbine, where a linearization strategy to represent the turbine dynamics is applied within the MPC. The choice of an MPC strategy relies on the fact that the methodology is able to address the gas turbine constraints (surge region, inlet temperature, maximum valve opening, valve open/close speed) explicitly in the optimization procedure. Therefore, the MPC algorithm ensures that variables will not violate the constraints [2].
Since then, as stated by Pongrácz et al. [24], there have been few works related to MPC applied to gas turbines, most of them employing models built on linearization techniques, rather than first principle models. Jurado and Carpio [25] applied Hammerstein model. Some experiments of MPC were conducted by van Essen and de Lange [26] applying successive linearization techniques to model a laboratory gas turbine installation. Brunell et al. [27] employed MPC to an aircraft gas turbine engine also using linearization technique, to which the authors refer as Simplified Real Time
Model (SRTM). Mu and Rees [28] named their control strategy as Approximate Model Predictive Control (AMPC), in which the linearization technique is employed. Martucci et al. [29] studied the effects of terminal weight on the prediction horizon of a gas turbine engine using a linear model within MPC strategy. Brunell et al. [30] applied MPC based on successive linearization approach to an aircraft engine. Mu and Rees [31] compare an MPC strategy with repeated linearization concept with a strategy which uses a model built with use of neural network identification technique. Ghorbani et al. [32] used a linear model in a multivariable MPC strategy for a gas turbine power plant and the same authors used a linear model in a constrained MPC strategy for a heavy-duty gas turbine power plant [33]. Lusanga [34] investigated the availability of MPC for a Brayton cycle represented by a linear model.
In recent years, some remarkable results have been obtained with MPC strategies applied to complex nonlinear systems [35]. In this context, the present work uses DESTUR [8] to represent the nonlinear dynamic behaviour of the gas turbine. The process simulator solves the equations of state and the conservation equations of mass, energy and momentum.
The class of MPC controllers adopts the following overall methodology. The process model is used for predicting future outputs, for a given horizon Nh. The predicted outputs ŷ (t + k|t), k = 1, 2 ... Nh, depend on the knowledge of the input and output values at the time (t), and on the set of future control signals u(t + k|t), k = 1, 2 ... Nh, which must be evaluated and sent to the system, as illustrated in Figure 1.
Overall MPC strategy
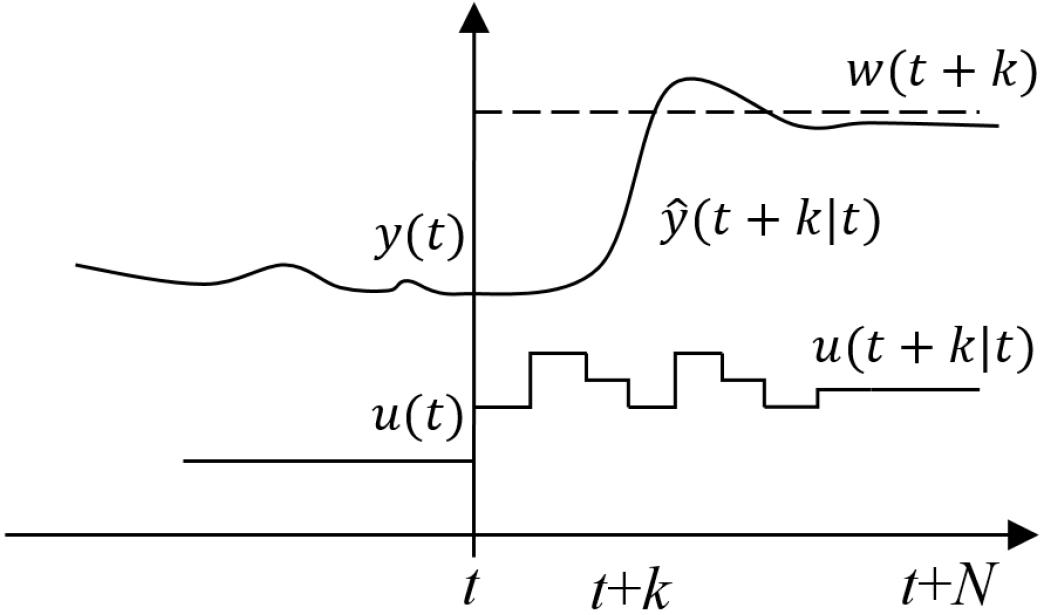
The set of u is obtained by optimizing a criterion established to keep the process as close as possible to a reference trajectory (t + k), which may be the actual desired value (set-point), or an approximation of it. In general, this criterion is a quadratic function of the error between ŷ and w, as adopted in this work. Usually, the control effort Δu is also considered in the objective function.
If the model is linear, a quadratic criterion is used, and no restriction is considered. As a consequence, it is possible to attain an explicit solution for the optimization problem, i.e., one can obtain a direct equation for the control signals (u). In the present work, since a nonlinear model as well as restrictions are considered, an optimization method is used to find a solution. The optimization algorithm plays an important role in this strategy, and its effort depends on the number of variables and restrictions, and on the size of the predictive horizons.
The model predictive control is formulated as the repeated solution of an optimal control problem with finite horizon open loop, subjected to the system dynamics, input constraints and state restrictions, as shown in Figure 2.
MPC general structure
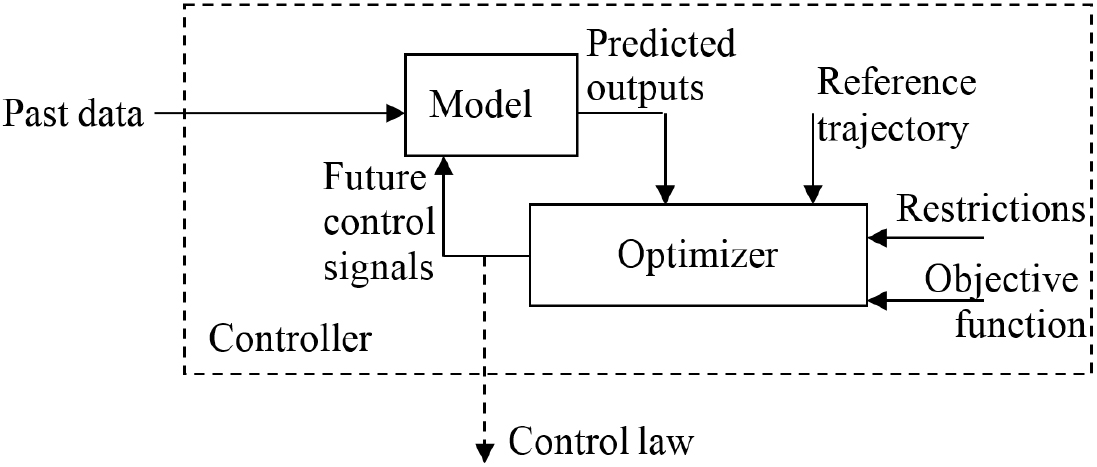
Thus, the choice of the model is critical to the quality of the outputs prediction.
The class of MPC controllers adopts the following overall methodology. The process model is used for predicting future outputs, for a given horizon Nh. The predicted outputs ŷ (t + k|t), k = 1, 2 ... Nh, depend on the knowledge of the input and output values at the time (t), and on the set of future control signals u(t + k|t), k = 1, 2 ... Nh, which must be evaluated and sent to the system, as illustrated in Figure 1.
Different objective functions may be proposed to obtain the control law (u). However, the general idea is to impose the future outputs (ŷ) to follow the desirable path (w) within the considered horizon, while the control effort (∆u) necessary to perform such a task is penalized. Therefore, in this work the objective function is expressed according to:
where N1, N2 and Nu mean, respectively, minimum prediction horizon, maximum prediction horizon and control horizon. The parameters N1 and N2 establish the period that the predicted outputs (ŷ) must follow the reference (w). The parameters δ and λ are coefficients that penalize future behaviour.
One advantage of predictive control is when the reference trajectory (w) is known a priori, because then the system can effectively react before any change has occurred. Such anticipatory feature avoids the delay effects on process response. In process optimization, most methods use a reference trajectory that does not necessarily correspond to the actual reference r(t), such that w is a smooth approximation of r, as given by:
The closer the value of α is to 1, the smoother is the approximation.
In practice, all processes are subjected to restrictions, whether constructive, safety, environmental, operational or economic constraints. Furthermore, process variables changes can be bounded, for instance, due to the physical limits of the actuators. Usually, instruments limitations influence the amplitude and rate of change of the control signal, as well as the output boundaries, which can be represented by the following rules:
where ∆u = u(t) – u(t – 1). Adding constraints increases complexity of the algorithm, such that an explicit solution cannot typically be obtained.
Control signal u(t + k|t) is obtained by minimizing the objective function (J). To optimize J the predicted outputs ŷ (t + k|t) must be evaluated based on a mathematical model. Whatever method is used to search for u, there will be (N2 – N1 + 1) independent variables. To reduce the number of degrees of freedom, one assumes that the control law is such, that after a given time Nu (< N2) there are no changes in control signals, according to the following rule:
The previous assumption implies that the second term of the J expression in eq. (1) will be a summation up to Nu, and brings improvement to the robustness and overall behaviour of the system. In fact, the free evolution of the manipulated variables can lead to undesirable control signals with high frequency and, in the worst case, instability.
The MPC strategy is applied to the speed (N) control of a compressor as the gas turbine load changes, by manipulation of the fuel flow (ṁf) into the combustion chamber. Thus, the control law (u) is the fuel flow, while the output (y) is the compressor speed. The thermal system considered in this study is a gas turbine consisting of seven components, as shown in Figure 3.
Scheme of the gas turbine configuration
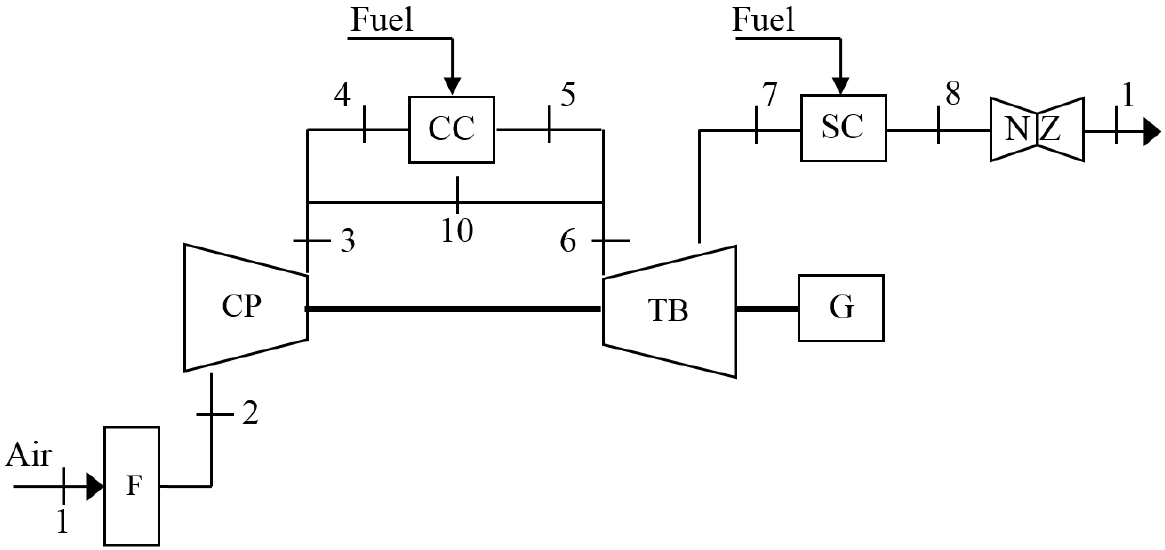
The turbine represents a commercial industrial configuration, and the simulation is accomplished by the program DESTUR. In Figure 3, the components F, CP, CC, TB, G, SC, and NZ represent, respectively, filter, compressor, combustion chamber, turbine, generator, supplementary combustor and nozzle.
As shown in Figure 4, each component is represented in DESTUR as a module.
Gas turbine representation in the program DESTUR
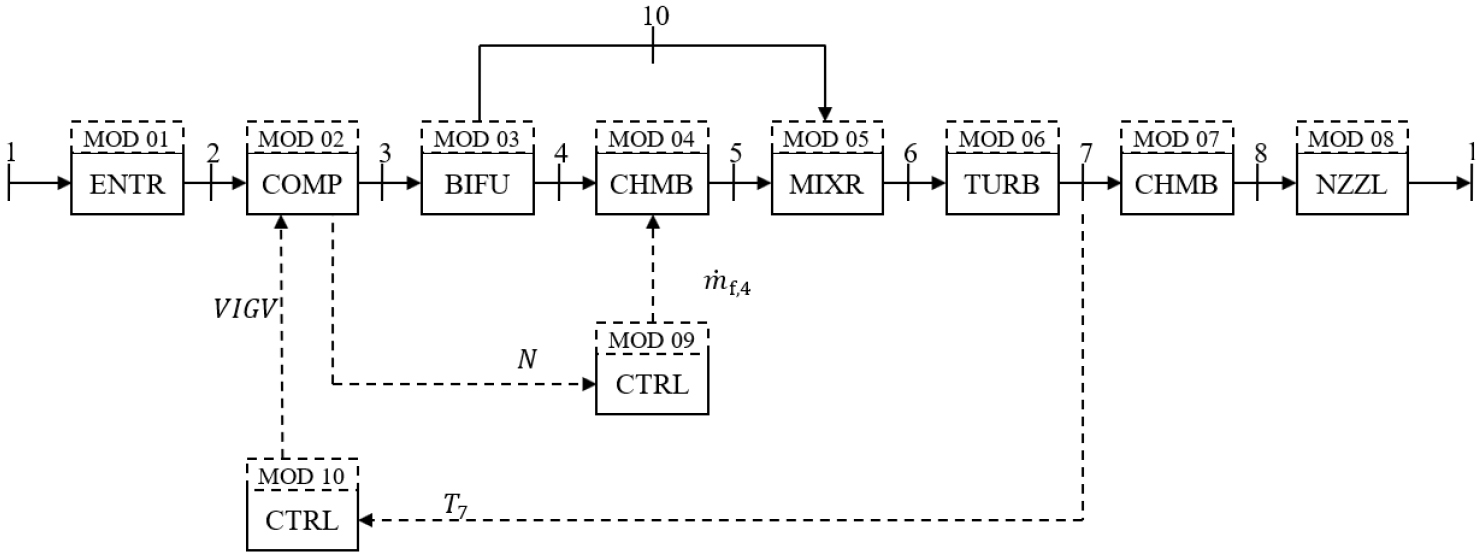
The parameters for each module must be defined. Indeed, the program has a modular structure, which allows for the implementation of different turbine configurations. The data input procedure is performed by creating a ‘.dat’ file. The program output is also delivered in the same file extension. The MPC is implemented in MATLAB®, which reads and writes ‘.dat’ files for communication with DESTUR. Within the MPC, during optimization procedure, the objective function is evaluated several times, and at each time DESTUR is called.
Additionally, Figure 4 illustrates two independent PID control loops: one that manipulates fuel flow in CC, and another that manipulates the VIGV. This work substitutes the PID loop by an MPC strategy to control compressor rotation by managing fuel flow in CC.
To assess the performance of the control strategy, a load rejection scenario is simulated. The load rejection test is undertaken during commissioning of a gas turbine, to evaluate the speed control in case of a sudden load fall without emergency trip of the turbine. An acceptance criterion of such test is that the speed shall not exceed 10% of its nominal value [36].
For the optimization problem which is part of the MPC strategy, computation of the gradient may not be feasible or cost-effective when using a nonlinear model, such that search methods or heuristic methods become attractive. Genetic and evolutionary optimization algorithms have been employed to search for the optimal solutions of realistic thermal systems, as in Manolas et al. [37] where a genetic algorithm is applied for the operation optimization of a cogeneration system, which supplies a process plant with electricity and steam, and as in Pires et al. [38] where evolutionary algorithms are applied to achieve thermoeconomic optimization of a complex cogeneration system.
Here, the objective function (J) is minimized by means of the stochastic heuristic method of differential evolution [9]. In addition to the quadratic error of predicted outputs and to the control effort, the objective function also considers the manipulated variable, i.e., fuel consumption in combustion chamber (ṁf), such that during the steady-state mode the gas turbine operates burning as little fuel as possible and still delivering the desired output (N). Therefore, the considered objective function is obtained by adding the fuel flow rate term (ṁf), to the right-hand side of eq. (1).
The MPC strategy is implemented coupled to DESTUR. In Figure 4, it is represented by the module “MOD 09”, which is responsible for the compressor rotation control by manipulating fuel flow (ṁf) in the CC. The control purpose is to maintain the compressor speed (N) at 3,600 rpm. Control parameters are presented at Table 1.
Comparison between theory and experiment
Parameter |
Value |
|---|---|
∆umin [kg/s] |
0.0 |
∆umax [kg/s] |
2.0 |
umin [kg/s] |
2.0 |
umax [kg/s] |
10.0 |
α |
0.0 |
W [rpm] |
3,600 |
N1 |
1 |
N2 |
4 |
Nu |
2 |
λ |
1.0 |
δ |
0.5 |
Ts [s] |
0.5 |
To verify the dynamic behaviour and control performance, the MPC is tested under three situations.
In the first scenario, the MPC algorithm is applied during the steady-state regime with the purpose of finding the best values for fuel flow, while maintaining rotation at the desired level, say 3,600 rpm. During operation with constant power output of 107 MW, as illustrated in Figure 5, after 10 seconds the fuel flow is gradually optimized from 6.90 kg/s to 6.88 kg/s, while the rotation is controlled at 3,600 rpm.
Results for fuel consumption optimization: controlled and manipulated variables
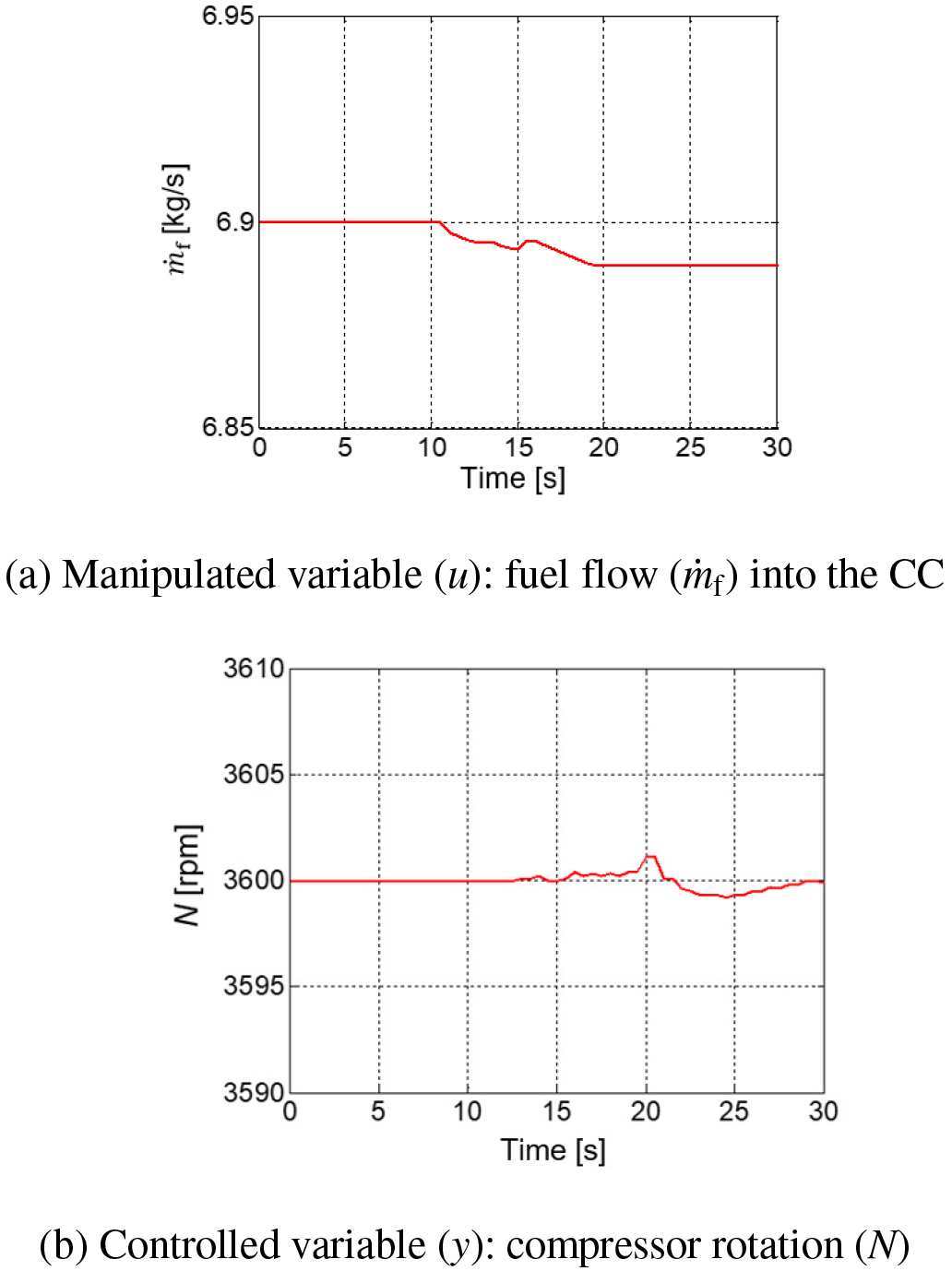
Thus, as demonstrated, there are other possible operating points for the same rotation of the compressor. In this example of a sustainability-related tactic, the MPC controller was able to select an operating point with reduced fuel consumption while maintaining the desired rotation.
For the second case, step disturbances in the load of the gas turbine are applied. At first, a sudden load fall of 10% is imposed, reducing it from 107 MW to 96.3 MW, as shown in Figure 6.
Load removal/addition
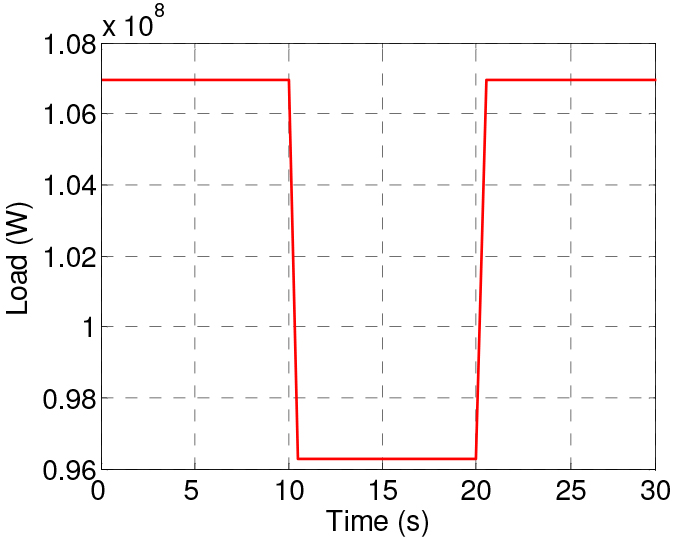
After load removal, the turbine operation stabilizes. Subsequently, another step change is forced, but now the load increases back to its original value. As expected, during the first change in load, rotational speed increases, as illustrated in Figure 7b.
Results for load removal/addition: controlled and manipulated variables
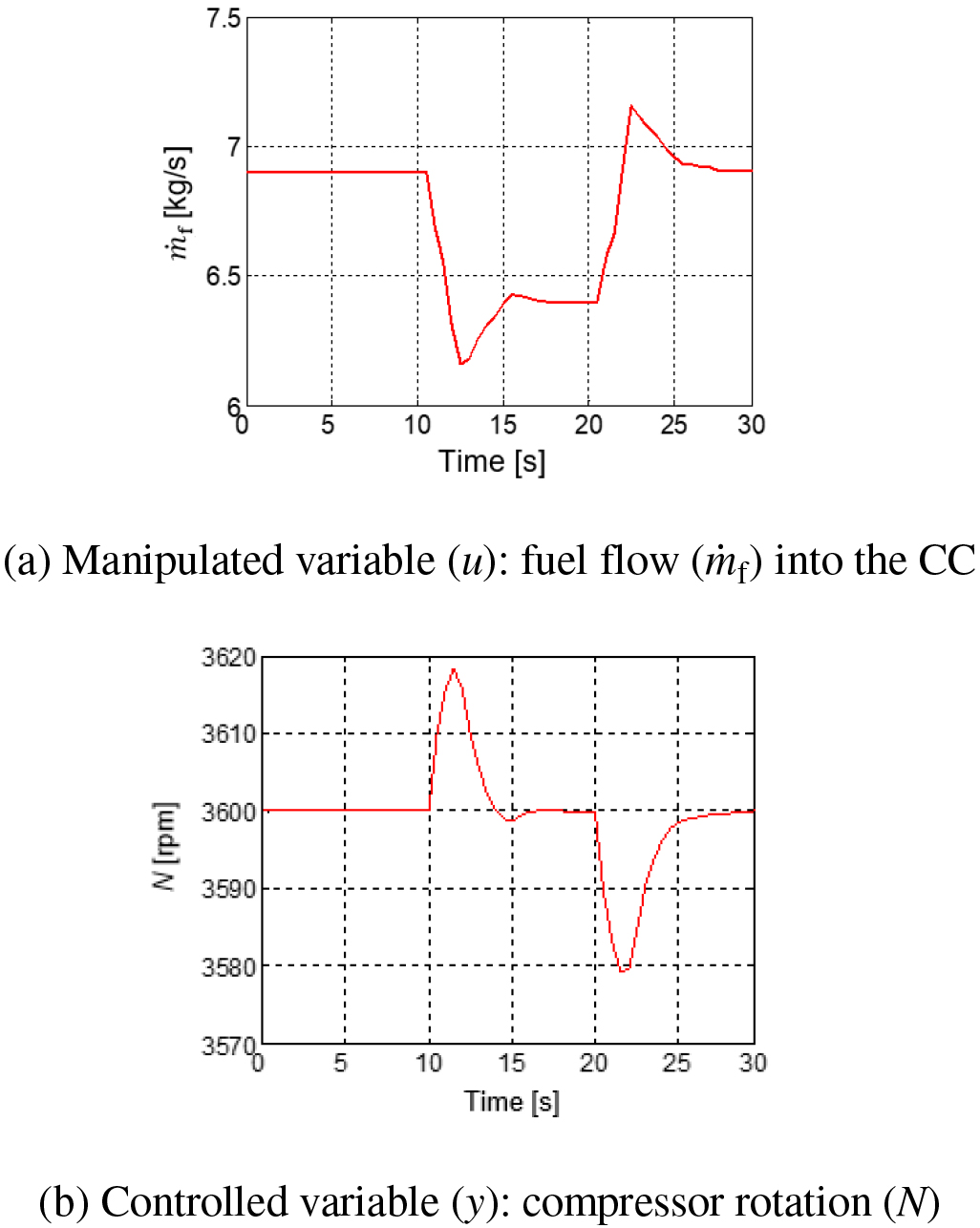
As the compressor rotation (N) offsets its set-point of 3,600 rpm, the MPC looks for the best values of fuel flow (ṁf) into the combustion chamber, aiming to control the shaft speed (N). Consequently, the fuel flow is automatically operated on by the MPC, as demonstrated in Figure 7a. Thereby, fuel flow is reduced, and then stabilizes, while rotational speed is controlled (3,600 rpm). After stabilization, load is added back, decreasing rotation. The MPC thus promptly acts, increasing fuel flow until the rotation set-point of 3,600 rpm is achieved. Eventually, the operation stabilizes once again, and the turbine runs in a steady-state regime.
The third and last scenario is a load rejection, i.e., a sudden load fall related to power failure due to a lightning strike or mechanical failure. In this case, as shown in Figure 8, the power output of 107 MW to the grid is unexpectedly lost at 10 seconds.
Load rejection
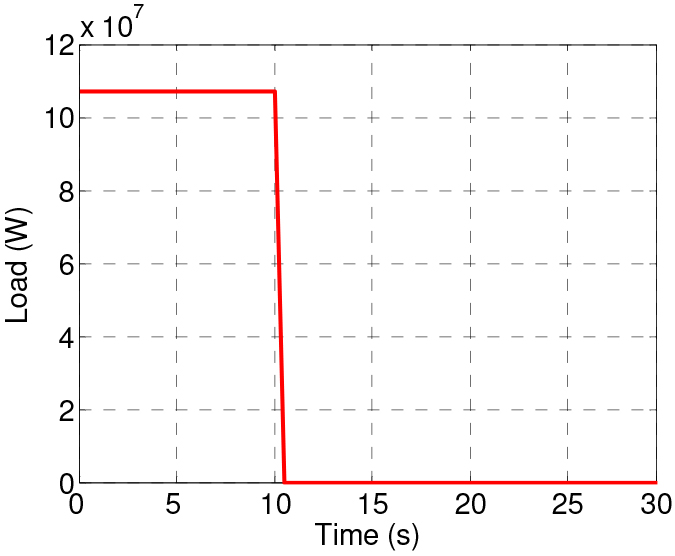
As a consequence, as indicated in Figure 9a, the compressor speed achieves 3,832 rpm, within 10% of its nominal value.
Results for load rejection: controlled and manipulated variables
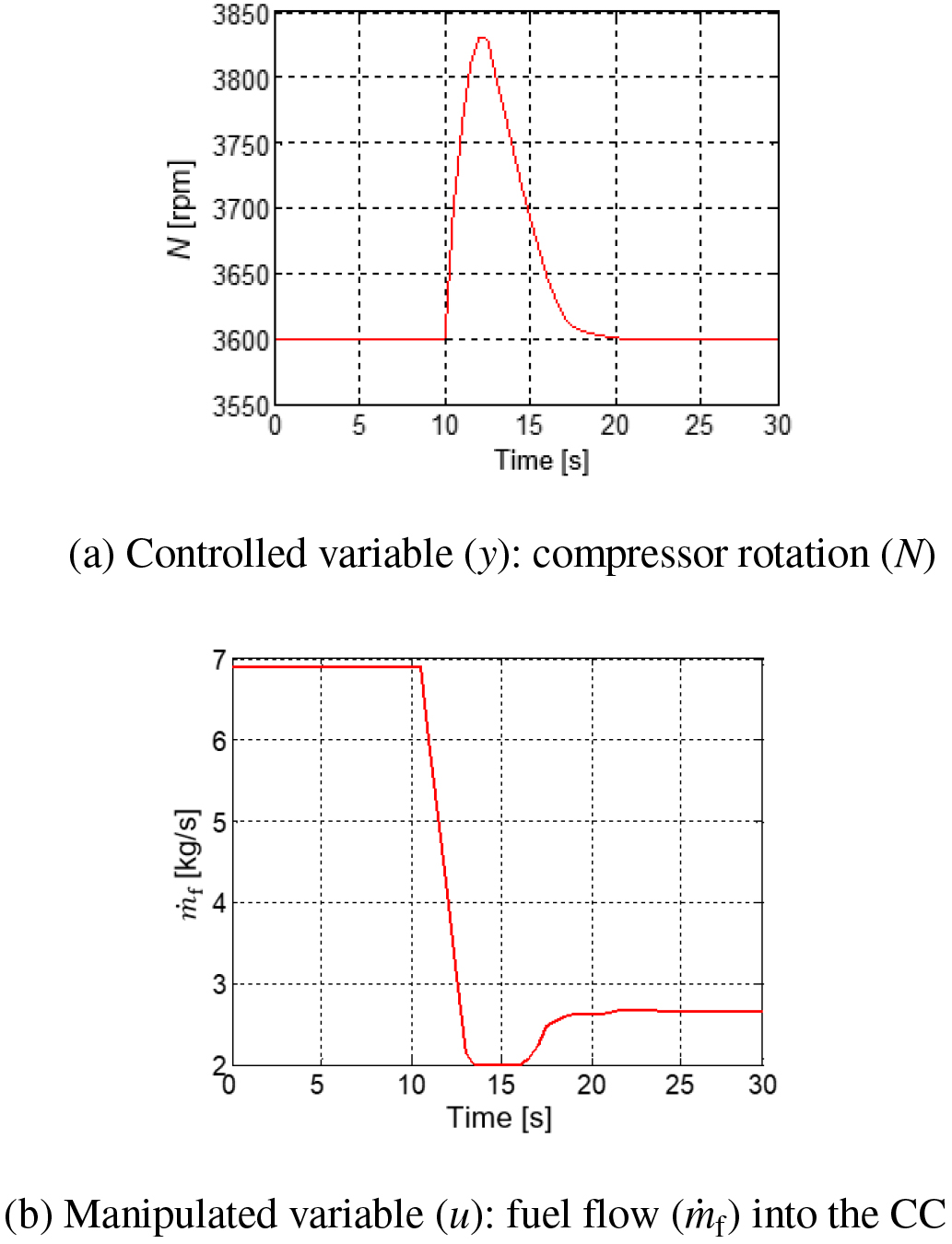
As per Figure 9b, fuel flow is rapidly manipulated downwards, such that the speed goes back to 3,600 rpm in the course of the next 11 seconds.
This work has proposed a nonlinear MPC strategy to control the compressor rotation of a gas turbine during load changes. The methodology has been successfully applied, in conjunction with an evolutionary optimization technique, to control a gas turbine during transient operating mode, and to optimize fuel consumption during steady-state mode. Through the optimization procedure the nonlinear MPC is able to explicitly handle the process constraints, and therefore the gas turbine operation is controlled in a safe and cost-efficient manner.
The use of a first principle simulator in the model-based predictive control strategy has proven capable to consider all nonlinearities of the physical and thermodynamic constraint equations, in as much as all necessary libraries are built-in. Furthermore, the simulator brings flexibility to the analysis, since it allows for quick modifications in the equipment and connections.
Finally, as an indication of forthcoming research, it is intended to implement the MPC strategy to manipulate both fuel flow and air flow in a single loop. A hierarchical implementation, where the actions of decentralized controllers are managed by an algorithm operating at a higher level, is also a subject for future research.
- ,
Aeronautics Institute of Technology ,D.Sc. Thesis , 2003 - ,
Model Predictive Control of a Gas Turbine installation ,WFW Report 97.002 , 1997 - ,
Fuzzy-predictive direct Power control implementation of a Grid connected Photovoltaic System, associated with an active Power Filter ,Energ. Convers. Manag. , Vol. 122 (15), :515-5252016, https://doi.org/10.1016/j.enconman.2016.06.018 - ,
Development of a Method of Real-time Building Energy Simulation for efficient predictive Control ,Energ. Convers. Manag. , Vol. 113 (1), :220-2292016, https://doi.org/10.1016/j.enconman.2016.01.060 - ,
Model predictive Control-based efficient Energy recovery Control Strategy for regenerative braking System of Hybrid Electric Bus ,Energ. Convers. Manag. , Vol. 111 (1), :299-3142016, https://doi.org/10.1016/j.enconman.2015.12.077 - ,
Decentralized Model predictive based load Frequency Control in an interconnected Power System ,Energ. Convers. Manag. , Vol. 52 (2), :1208-12142011, https://doi.org/10.1016/j.enconman.2010.09.016 - ,
Nonlinear Model predictive Control: From Theory to Application ,J. Chin. Inst. Chem. Engrs. , Vol. 35 (3), :299-3152004 - ,
A Step further in Gas Turbine dynamic Simulation ,Proc. Instn Mech. Engrs., Part A: J. Power and Energy , Vol. 217 (6), :583-5922003, https://doi.org/10.1177/095765090321700606 - ,
Differential Evolution – A simple and efficient adaptive Scheme for Global optimization over continuous Spaces ,Report No.: TR-95-012 , 1995 - ,
Comparative analysis of stochastic and Pattern search methods applied to Thermoeconomic optimization of a complex Cogeneration System modeled in a Process Simulator ,Proceedings of Inverse Problems, Design and Optimization Symposium , 204-2112010 - ,
Advanced Controls for Fuel consumption and Time-on-Wing optimization in commercial Aircraft Engines ,ASME Turbo Expo 2007: Power for Land, Sea, and Air , Vol. 1 (GT2007-27214), :539-5482007, https://doi.org/10.1115/GT2007-27214 - ,
Nonlinear Model predictive Control of a Laboratory Gas Turbine installation ,Journal of Engineering for Gas Turbines and Power , Vol. 121 (4), :629-6341999, https://doi.org/10.1115/1.2818518 - ,
Modelling and Model based Control of Turbomachinery ,Ph.D. Thesis , 1998 - ,
A Method for estimating Speed response of Gas-turbine Engines ,Research Memorandum , 1952 - ,
Simulation of Gas Turbines performance during transient state ,M.Sc. Thesis , 2006 - ,
Simplified Mathematical representation of Heavy-Duty Gas Turbine ,Journal of Engineering for Power – ASME , Vol. 105 (4), :865-8691983, https://doi.org/10.1115/1.3227494 - ,
Simplified Mathematical representation of single Shaft Gas Turbines in Mechanical Drive Service ,Turbomachinery International , V005T15A0011992, https://doi.org/10.1115/92-GT-022 - ,
Gas Turbine identification with Linear and Non-Linear Techniques ,M.Sc. Thesis , 2005 - ,
Overview and comparative analysis of Gas Turbine Models for System Stability Studies ,IEEE Transactions on Power System , Vol. 23 (1), :108-1182008, https://doi.org/10.1109/TPWRS.2007.907384 - ,
Transient Performance modelling of a heavy duty Gas Turbine used for Power Generation ,Proceedings of 20th International Congress of Mechanical Engineering – COBEM , 2009 - ,
Transient Regime modelling of Industrial Gas Turbines for Power generation ,M.Sc. Thesis , 2010 - ,
Gas Turbine Control Strategy ,M.Sc. Dissertation , 2012 - , Gas Turbine Engineering Handbook (2nd ed.), Butterworth-Heinemann, 2002
- ,
Nonlinear Reference tracking control of a Gas Turbine with load Torque estimation ,International Journal of Adaptive Control and Signal Processing , Vol. 22 (8), :757-7732008, https://doi.org/10.1002/acs.1020 - ,
Improving distribution System stability by predictive Control of Gas Turbines ,Energ. Convers. Manag. , Vol. 47 (18-19), :2961-29732006, https://doi.org/10.1016/j.enconman.2006.03.028 - ,
Nonlinear Model predictive Control Experiments on a Laboratory Gas Turbine installation ,Journal of Engineering for Gas Turbines and Power , Vol. 123 (2), :347-3522001, https://doi.org/10.1115/1.1359478 - ,
Nonlinear Model predictive Control of an Aircraft Gas Turbine Engine ,Proceedings of the 41st IEEE Conference on Decision and Control , 2002, https://doi.org/10.1109/CDC.2002.1185111 - ,
Approximate Model predictive Control for Gas Turbine Engines ,Proceedings of the 2004 American Control Conference , Vol. 6 , :5704-57092004, https://doi.org/10.23919/ACC.2004.1384765 - ,
The Effect of terminal Weight on the prediction Horizon of a Gas Turbine Engine using Model predictive Control ,ASME Turbo Expo 2004: Power for Land, Sea, and Air , Vol. 2 , 2004 - ,
Model adaptation and Nonlinear Model predictive Control of an Aircraft Engine ,ASME Turbo Expo 2004: Power for Land, Sea, and Air , Vol. 2 , 2004 - ,
Advanced Controller design for Aircraft Gas Turbines Engines ,Control Engineering Practice , Vol. 13 (8), :1001-11152005, https://doi.org/10.1016/j.conengprac.2004.11.001 - ,
Multivariable Model predictive Control for a Gas Turbine Power Plant ,Proceedings of 10th WSEAS Int. Conf. on Automatic Control, Modelling & Simulation (ACMOS’08) , 275-2812008 - ,
Constrained Model predictive Control implementation for a heavy-duty Gas Turbine Power Plant ,WSEAS Transactions on Systems and Control , Vol. 3 (6), :507-5162008 - ,
Model predictive Control of a Brayton Cycle based Power Plant ,M.Sc. Dissertation, School of Electrical and Electronic Engineering , 2012 - , Model Predictive Control, Advanced Textbooks in Control and Signal Processing (2nd ed.), 2007
- ,
Gas Turbine Applications using ThermoFluid ,Proceedings of the 3rd International Modelica Conference , 359-3662003 - ,
Operation optimization of an Industrial Cogeneration System by a Genetic Algorithm ,Energ. Convers. Manag. , Vol. 38 (15-17), :1625-16361997, https://doi.org/10.1016/S0196-8904(96)00203-8 - ,
Response Surface Method applied to the Thermoeconomic optimization of a complex Cogeneration System modeled in a Process Simulator ,Energy , Vol. 52 , :44-542013, https://doi.org/10.1016/j.energy.2012.12.049