Biomass pyrolysis involves the heating of raw biomass or organic waste materials in the absence of an oxidizing agent, in order to extract reaction products for a latter application. The majority of early research in this field is focused on the low temperature low heating rate pyrolysis aimed at maximizing the char yields for production of charcoal fuel [1]. Among the thermo-chemical conversion methods, pyrolysis is the most suitable method to produce bio-oil as the main product, compared to gasification and combustion [2]. Slow pyrolysis can be divided into traditional charcoal making and more modern processes. It is characterized by the slower heating rates, relatively long solid and vapor residence times and usually uses a lower temperature, contrary to the fast pyrolysis. In slow pyrolysis processing, the target product is often the char, but this is always accompanied by gas products analysis. On the other hand, fast pyrolysis is characterized by high heating rates (≥ 1,000 °C s-1)/high temperatures, and short vapor residence times. This approach generally requires a feedstock prepared as small particle sizes and a design that removes the vapors quickly from the presence of the hot solids [3] to give significantly lower yields of oil and char compared with slow pyrolysis [4]. These conditions are aimed at maximizing tar and gas yields while simultaneously minimizing char formation [5]. Optimal pyrolysis conditions for various applications remain largely uncertain and accurate mathematical models are needed to aid in the design of scalable and efficient biomass conversion reactors [6].
Biomass is generally composed of three main groups of natural polymeric materials, such as: cellulose, hemicelluloses, and lignin (called biomass pseudo-components). Other typical components are grouped as extractives' (usually represents smaller organic molecules or polymers) and minerals (the inorganic compounds). These are present in differing proportions in a various types of biomass, and these proportions influence the product distributions on the pyrolysis process [7]. During heating in the pyrolysis temperature ranges, the following main pseudo-components contribute to product yields, such as: primary products of hemicelluloses and cellulose decompositions are condensable vapours (hence the liquid products) and gas. Afterwards, lignin decomposes to liquid, gas, and solid char products. In addition, the extractives' contribute to liquid and gas products either through the volatilization or decomposition. The minerals usually remain in the char, where they are termed ash. The vapours formed by the primary decomposition reactions of the biomass pseudo-components (cellulose, hemicelluloses, and lignin) can be involved in the secondary reactions in a gas phase, forming soot, or at hot surfaces, especially hot char surfaces, where the secondary char is formed. This issue is particularly important in understanding the differences between the slow and fast pyrolysis and factors affecting the char yields [8].
Rising industrialization and the reduction of energy reserves have led to research into new technologies that would apply renewable, easily accessible and economically viable waste materials. In the last few decades, waste agro-industrial lignocellulosic biomass has been the subject of numerous researches around the world due to its wide distribution, low cost, reproducibility and structural characteristics [9]. This paper focuses on the thermal conversion study related to the slow pyrolysis devolatilization kinetics of the waste lignocellulosic biomass that reflects on its energy characteristics. For this purpose, the waste lignocellulosic biomass, the apricot (Prunus armeniaca) kernel shells was used. It should be noted that testing the devolatilization kinetics and appropriate kinetic modelling, in the case of slow pyrolysis process of apricot kernel shells are not available in the literature. In contrast, the pyrolysis of apricot kernel shells (with heating rates of 10-50 °C min-1 and in static atmosphere incorporating sweep gas flow rates of 50-200 cm3 min-1) (Turkey apricot variety) was performed in the literature, but in order to determine the main characteristics and quantities of liquid and solid products [10]. The work [10] was focused on the effects of pyrolysis temperature, heating rate, and sweeping gas flow rate on the product yields, as well as to the characterization of the obtained bio-oil, and the characterization of the chars as solid products for possible use of solid fuels or activated carbon. Namely, most of the studies related to stone-fruiting waste lignocellulosic biomass are focused on the char, the solid, residual product of pyrolysis [11], which could be harnessed for energy production or for production of low-cost adsorbents [12]. Also, this type of waste biomass could be utilized for the production of biogas, for example by pyrolysis of the soft shell of pistachios [13].
The main goal of this research represents showing the most probable devolatilization kinetics during slow pyrolysis process of raw apricot kernel shell samples, which is monitored by simultaneous Thermogravimetric Analysis (TGA) – Differential Thermal Analysis (DTA) techniques, coupled with Mass Spectrometry (MS) technique, for analysing the gas products at the various heating rates, in a dynamic, linear regime of heating. The complete description of devolatilization kinetics of apricot kernel shells during slow pyrolysis was made possible by application a new proposed multicomponent modelling using combined “model-free” kinetics and multi-dimensional nonlinear regression analysis performed in MATLAB software program. The “model-free” methods [14] (such as Berčić [15], Kissinger [16], Kissinger-Akahira-Sunnose (KAS) [17], Ozawa [18] and Ozawa-Flynn-Wall (OFW) [19] methods) were used in order to check the complexity degree of the process (one-step or multi-step kinetics ‒ assuming that the pyrolysis process of the waste lignocellulosic biomass is complex caused by the interaction of devolatilization, diffusion effect, catalyst, and secondary reactions [20]), while implementing the Objective Function (OBF) minimization procedure provides reliable determination of the kinetic parameters, forming the entire model of apricot kernel shell pyrolysis.
To accurately comprehend the course of reaction progression, knowledge of kinetic parameters (triplet) is crucial, especially for the complex reactions like biomass decomposition that is being researched for scale-up and process optimization. The techniques for kinetic analysis of biomass are more obscure compared with other solid-state reactions, owing to the complexity of the feed. In this work, an advanced kinetic methodology that gives on the significance of the kinetic triplet and allows the pursuit of reliable kinetic parameters was developed. The presented approach is capable for working on the multi-step reactions, involved in the thermal decomposition of assorted biomass.
The apricot kernel shells as waste lignocellulosic biomass residues originating from a local fruit processing plant were used. The sample preparation was done according to standard procedure [21] and further sample was tested in order to obtain data of ultimate and proximate analyses in accordance with the relevant standard [22]. Furthermore, the prepared sample was also used for the Simultaneous Thermal Analysis (STA) which provides data for TGA and DTA simultaneously on the same sample.
The NETZSCH STA 445 F5 Jupiter system was used for STA measurements under the following conditions:
Sample mass: 5.0 ±0.3 mg;
Temperature range: from room temperature up to 900 °C;
Heating rate: 5, 10, 15 and 20 °C min-1;
Carrier gas: argon (the high purity – class 5.0);
Total carrier gas flow rate: 30 mL min-1.
The STA measurements were performed with alumina crucibles in order to achieve the optimal sensitivity of the Thermogravimetric (TG) signal and to clearly identify all mass losses during thermal decomposition of the considered sample.
Typical kinetic analysis of the thermal decomposition of lignocellulosic materials under the non-isothermal conditions is usually written in the form:
(1)
where α is the conversion degree which is dimensionless (the conversion degree increases from 0 to 1 during the process and reflects the overall progress of the reactant transition into the products), dα/dt is the rate of considered process, T is the absolute temperature, β = dT/dt is the heating rate, A is the pre-exponential factor, Ea is the apparent (effective) activation energy, R is the gas constant (8.314 J mol-1K-1), and f(α) is the conversion (reaction model) function (a solid state reaction model that depends on the controlling mechanism and the conversion degree). In the literature, a large number of reaction models can be found, however, they can all be reduced to three basic types, according to the form of dependence of the conversion degree, from time t or the temperature T: acceleratory, decelerator and sigmoid (autocatalytic) models [23].
By integrating eq. (1), the conversion function in a integral form, g(α), which describes the kinetic decomposition of biomass pyrolysis at the different heating rates can be achieved:
(2)
where x = (Ea/RT) is the reduced apparent activation energy, p(x) is the temperature integral and without analytical solution. Therefore, the eq. (2) can only be solved using either numerical integration or approximations in order to deal with this complex integral [24]. The expression for g(α) represents the fundamental model equation for isoconversional (“model-free”) kinetic decomposition of biomass species and deducing the kinetic parameters Ea and A. The solution to eq. (2) can be obtained from the Doyle’s approximation [25] which forms the theoretical basis for the isoconversional kinetic methods of Kissinger-Akahira-Sunose (KAS) [17] and Ozawa-Flynn-Wall (OFW) [19]. The isoconversional approach allows determination of Ea in a function of α, without considering the reaction model, f(α) or g(α). This group of methods most often involves performing the experiments at the different heating rates, whereby the kinetic parameters can be calculated for each selected conversion degree value, assuming that the reaction rate at a constant α is only a function of the reaction temperature. By implementing the Doyle’s approximation, the origin expression for OFW kinetic method is described by eq. (3):
(3)
where the apparent activation energy values Ea at various α values, can be calculated from the plot of ln(β) against 1/T at the different heating rates during TG tests. Each individual value of Ea can be calculated from the slope –1.052(Ea/R), where R takes the value 8.314 J mol-1K-1, while the pre-exponential factor (A), can be obtained for the exact analytical form of g(α) function. Likewise, applying the KAS isoconversional method to examine the pyrolysis decomposition of apricot kernel shell by applying the relation in the eq. (4):
(4)
the slope of the plot ln(β/T2) against 1/T produces the apparent activation energy for a specified value of α. After determining the Ea values for pyrolysis process, the pre-exponential factor A can be deduced only for the known analytical form of the g(α) function. The second type of isoconversional method, different from the previous two, is the differential isoconversional method proposed by Friedman (FR) [15] and which does not use any approximation for the temperature integral. This method was based on the logarithmic form of the eq. (1), and after re-arrangements is obtained:
(5)
From this equation, the first right-side member is constant, at a given β and α. Thus, the correspondent plot gives the straight lines with a slope that is directly proportional to the apparent activation energy Ea and, therefore, it can be derived from there. On the other hand, the pre-exponential factor A can be calculated from the exact knowledge of f(α) function.
In order to be more accurate in estimating the kinetic parameters using the above methods, the 95% confidence interval of estimation including Student’s test and Durbin-Watson (D-W) statistics related to autocorrelation in the residuals from a statistical regression analysis (D-W values and D-W factors) were used in error analysis. In all “model-free” methods, if the process follows a single-step mechanism, the respective apparent activation energies are expected to be similar. This means that it should not change considerably with conversions. In other words, the ‘isoconversional lines should have the same slope or just be parallel. A great change in the magnitude of these values with a change of α indicates the occurrence of a multi-step reaction(s) that definitely do not fit the single-step reaction mechanism and, therefore, cannot be analysed solely by the eq. (1). The last is the case when Ea does change with conversions as well as temperature. In such circumstances, a series of single step reactions is to be considered as taking place as the reaction degree improves. Provided that the experimental data are reliable, the dependence of Ea on α indicates a multi-step reactions process.
Considering the comprehensive structural composition of biomass, which is related to its origin and growth conditions, the multicomponent kinetic modelling approach was developed in order to cover all issues related to composition analysis [26]. Commonly the pyrolysis process has been simulated by a scheme consisting of several parallel reactions [27]. The exact number of considered reactions during kinetic modelling depends of type, origin and overall structure of the tested biomass sample [28]. According to already presented methodology the multicomponent kinetic modelling was applied for apricot kernel shell pyrolysis in order to identify the constitutive Pseudo-Components (PSCs) which could be of interest during the conversion process of the tested biomass samples [29].
The brief summary of the complete methodology used in this paper is shown in Figure 1, and is presented in detail in the literature [26].
Methodology flowchart used in this study [pseudo-component (PS), number of runs (P)] [26]
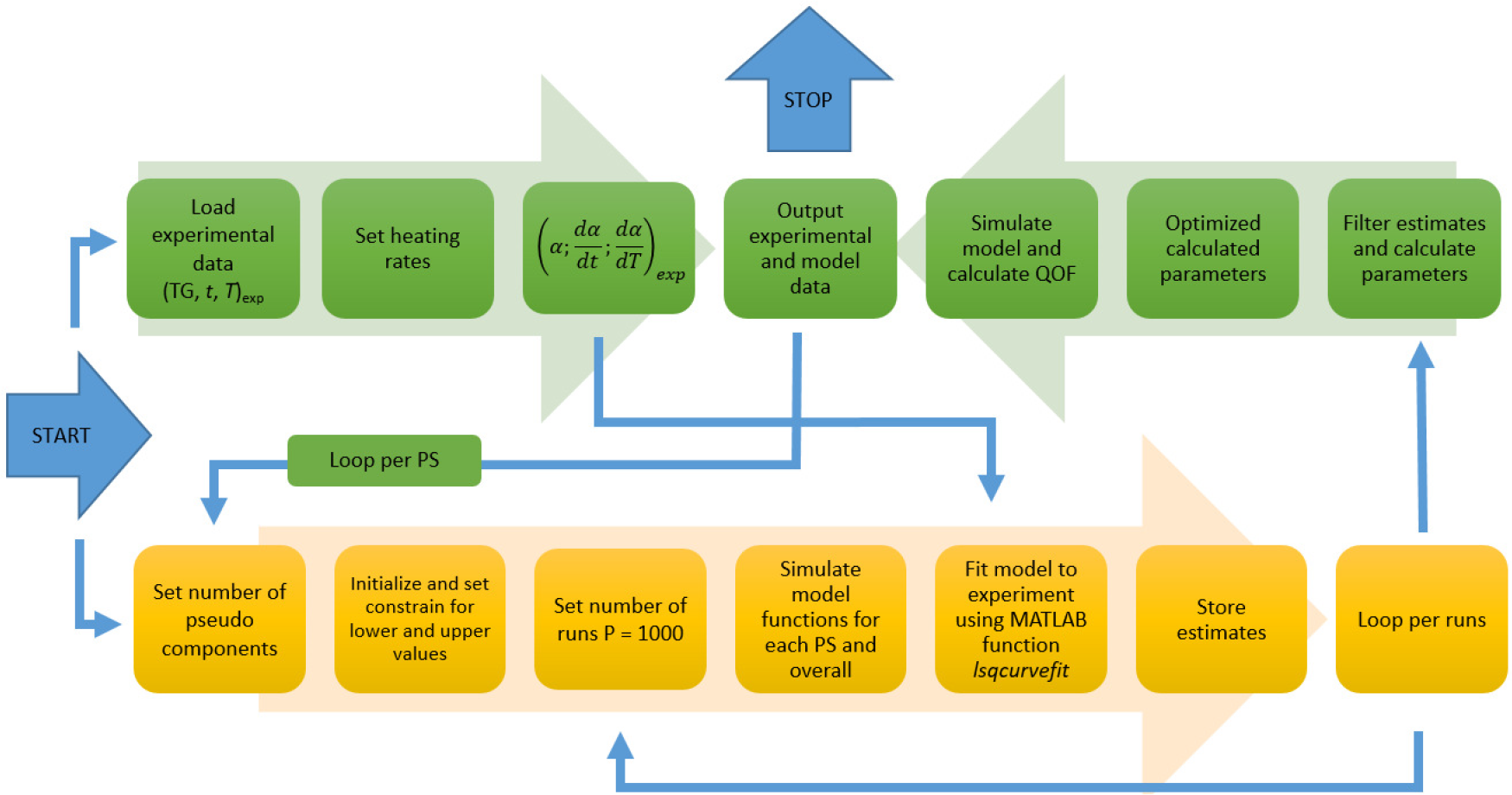
Application of the selected methodology together with peak to peak analysis approach could also provide calculation of kinetic parameters of each biomass PSC as well as pseudo-component fraction (Xi) at considered heating rate, which could be used for composition analysis of the selected material [30].
Table 1 shows the results of proximate and ultimate analysis of the raw apricot kernel shell samples studied in this work.
Results of proximate and ultimate analysis of raw apricot kernel shell samples
| Proximate analysis [wt%] | Ultimate analysisb [wt%] | ||
|---|---|---|---|
| Moisture | 9.71 | C | 46.88 |
| Volatile matter | 73.84 | H | 6.38 |
| Fixed carbon | 15.51 | Oc | 45.45 |
| Ash | 0.94 | N | 0.25 |
| HHV [MJ kg-1] | 20.26 | S | 0.00 |
| LHVa [MJ kg-1] | 18.72 |
Calculated according to [22]
On a dry basis
By difference
Considering the manufacturing process of various desirable products that arise from thermo-chemical conversion of biomass, which also involves the removal of volatile matter, the economic relationship between price, availability and quality of raw material on one side, and volatile content on the other side, are very important issues. From obtained results (Table 1), the volatile matter content of apricot kernel shell studied shows a high value (73.84%) which indicated that tested material produces more tar (the tars include any of several high molecular weight products that are volatile at pyrolyzing temperatures, but condense onto any surface near room temperature), having an impact on a lower percentage of fixed carbon. In this content, the fixed carbon content can be related to calorific value, since it has a positive effect on the energy potential of biomass. However, it should be noted that high volatile matter content does not guarantee high calorific value since some of the ingredients of volatile matter are formed from non-combustible gases such as carbon dioxide (CO2) and water vapour (H2O) [31]. For our sample, the content of volatile matter (Table 1) is close to volatile matter contents of red lentil hull (74.73%), broad bean husk (74.88%) and pea stem (74.67%) [32], the obtained value of volatile matter content is typical for herbaceous plant biomasses. As a result of fairly high volatile matter content may have consequences in the large quantities of gaseous products released during the process. In addition, the fixed carbon content (Table 1) is very close to those related to coconut shell (15.97%), almond shell (14.82%) and apple pulp (15.13%) [32]. However, the obtained content of fixed carbon of 15.51% suggests that apricot kernel shell can be used to obtain coke residue (solid bio-char), which would also indicate the material with good energy characteristics. On the other hand, the ash content of 0.94% (Table 1) is almost between the ash contents of elaeagnus (0.90%) and peach stone (0.97%) [33].
The obtained result is in very good agreement with ash contents related to the flowering plant biomass, just like apricot. The Higher Heating Value (HHV) for apricot kernel shell (Table 1) almost coincides with HHV value related to coconut shell (20.24 MJ kg-1) and peach (Prunus persica L.) stones (20.50 MJ kg-1) [32], so the estimated value belongs to those HHV values that have heat values greater than some known agricultural wastes, and falls within the limit for production of steam in electricity generation [33]. On the other hand, the moisture content of biomass affects its processing for applications such as electricity or steam. Also, the moisture content can have different effects on the pyrolysis product yields depending on conditions. The obtained value of apricot kernel shell moisture content (9.71%, Table 1) is lower than those typical for wood moisture content (15-20%) [7].
Therefore, the moisture in the reaction affects the char properties and this has been used to produce activated carbons, through the pyrolytic process of biomass. So, based on the estimated moisture content value (Table 1), a fairly dry feedstock (around 10%) was obtained, and this is an acceptable value considering that slow pyrolysis is more tolerant of moisture, since the main issue is related on its effect on the process energy requirements. From the ultimate analysis, a dominant contribution of carbon (46.88%) and oxygen (45.45%) (Table 1) can be noticed and this is in good agreement with the typical ranges of these elements in most biomass samples (40-60% for C, and around 45% for O) [34]. In addition, the concentration of nitrogen (N) is very low (0.25%, Table 1), while the concentration of sulphur (S) drops at zero, which is particularly important if apricot kernel shells combustion is considered, and with it, the emissions of harmful gases of nitrogen and sulphur oxides.
The simultaneous Thermogravimetric Analysis (TGA) – Derivative Thermogravimetry (DTG) curves in an argon atmosphere at heating rates of β = 5, 10, 15 and 20 °C min-1 are shown on Figure 2a-d.
At all observed heating rates, after the mass loss (TG-%) up to a temperature of approximately 120 °C which can be attributed to removing of moisture (in the range of 3.00-3.41% and this amount of mass loss was recorded due to loss of water present in the sample and external water bound by surface tension), the non-isothermal decomposition of apricot kernel shell occurs through four successive processes accompanied by designated mass losses in Figure 2a-d. Then in the temperature range from 120 °C to approximately 150 °C, the shells do not undergo any transformations that change their mass.
Simultaneous TGA-DTG curves in an argon atmosphere at β = 5, 10, 15 and 20 °C min-1 for apricot kernel shell pyrolysis (a-d)
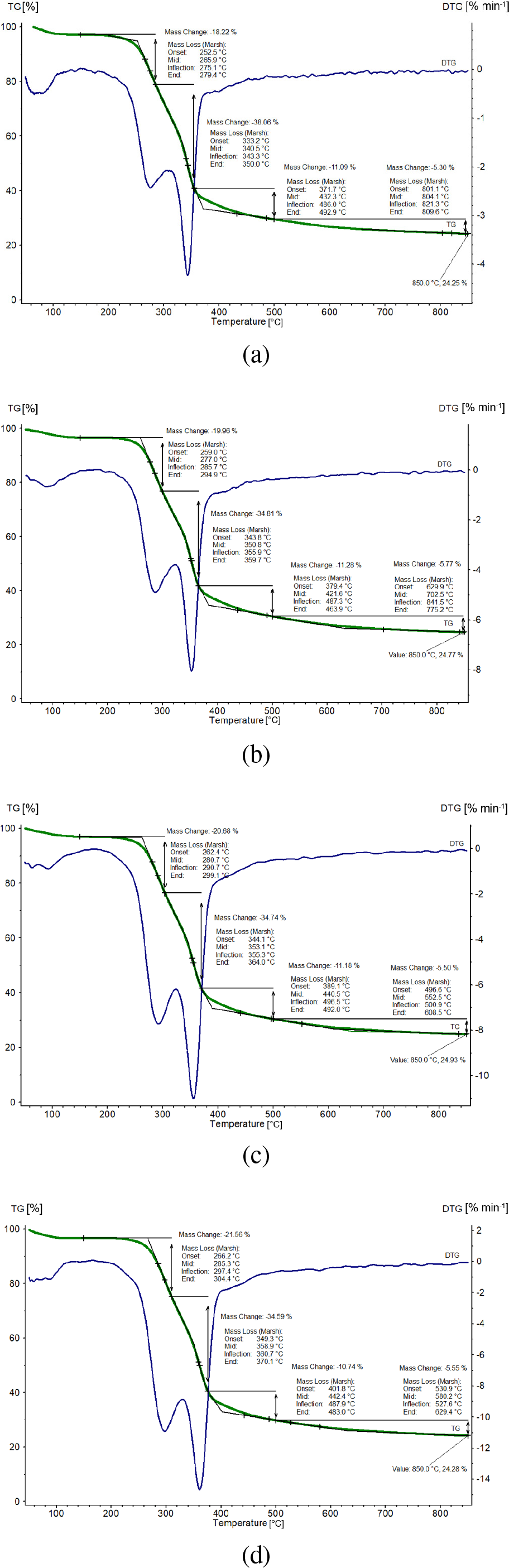
Above the indicated temperature (150 °C), the thermal stability of apricot kernel shells gradually decreases, and decomposition takes place (Figure 2a-d). The decomposition begins with extracting the volatile products that respectively accompanied by mass reduction. The total mass loss completes at about 850 °C, with residual mass loss in the range of 24.25-24.93% considering all heating rates. Since the apricot kernel shells represent the lignocellulosic material, the devolatilization process includes the decomposition reactions of the basic structural components of lignocellulosic biomass. The first two stages include decomposition of structural polymers, mainly hemicelluloses and cellulose [10] in the temperature range of 250-360 °C with about 56.28% in the largest mass loss of the sample (Figure 2a-d). The third stage can be attributed to the slow decomposition of aromatic polymer (lignin), which decomposes in the widest temperature range [35]. In a general manner, in accordance with results reported by Gasparovič et al. [36], the thermal decomposition of lignocellulosic material takes place in three main stages: evaporation of moisture and light hydrocarbons, active and passive pyrolysis. The decomposition of hemicelluloses and cellulose takes place through active pyrolysis in the temperature ranges of 160-305 °C and 305-370 °C, with temperatures at the maximum rate of mass losses as Tp1 = 285.7 °C and Tp2 = 355.9 °C (considering the values attached to β = 10 °C min-1, where “1” and “2” are attributed to hemicelluloses and cellulose, respectively) (Figure 2). The lignin decomposes in both stages, in active and passive pyrolysis zones, in the range of 160-900 °C, without a clearly expressed characteristic DTG peak (Figure 2a-d). The pyrolyzable fraction of this pseudo-component starts its devolatilization at the lowest temperature, but it is decomposed in a wide temperature range. The lignin decomposition is hindered by decomposition of hemicelluloses and cellulose, excepting at high temperature (especially in the temperature range of 380-480 °C, Figure 2a-d). These issues are clearly evidence for existence of multi-step process, which is typical for behaviour of complex reactions, involving the multiple, parallel, and consecutive processes during the decomposition of lignocellulosic biomass under inert atmosphere [37]. The effect of increase in heating rate can be observed in the DTG curves of studied biomass sample, during pyrolysis process. In actual case, the increase resulted in an enlargement of the curves resulting in the shifts in the size of the DTG curves, and changes in the main temperature profile characteristics for apricot kernel shell: Tonset, Tp (inflection) and Tend (Figure 1).
It can be seen that pyrolyzable fraction of hemicelluloses has much lower thermal stability than celluloses pyrolyzable fraction. In addition, the char fractions decompose at the higher temperatures (above 500 °C), with the hemicelluloses non-pyrolyzable fraction being the one that is burnt at lower temperatures, followed by the cellulose char. Lignin char was decomposed at the highest temperature and its yield may be very high. However, in this case, the analysis is especially difficult due to the formation of complex phenolic species during lignin decomposition. This behaviour has been previously reported by other authors [38]. In addition, the heating rate affects the rate of volatile evolution from biomass sample. It can be observed from DTG curves (Figure 2) that higher heating rate above 300 °C promotes rapid evolution of volatiles. The molecular disruption is extremely fast and volatile fragments are released so rapidly that successive adjustments and the equilibrium leading to further primary reactions that yield char have less opportunity to take place. As the heat rate increases, the amount of volatiles released increases.
The DTA curves of apricot kernel shell pyrolysis at the various heating rates (βj, j = 1, 2, 3, 4) and at one (selected) specific heating rate value (β = 10 °C min-1) are shown in Figure 3a-b.
According to Figure 3a-b, the initial drop over 40 °C to 120 °C (Figure 3b) is due to moisture evaporation, which is an endothermic reaction.
The DTA curves of apricot kernel shell pyrolysis at the various heating rates (a) and the DTA curve at one selected heating rate value (10 °C min-1) (b)
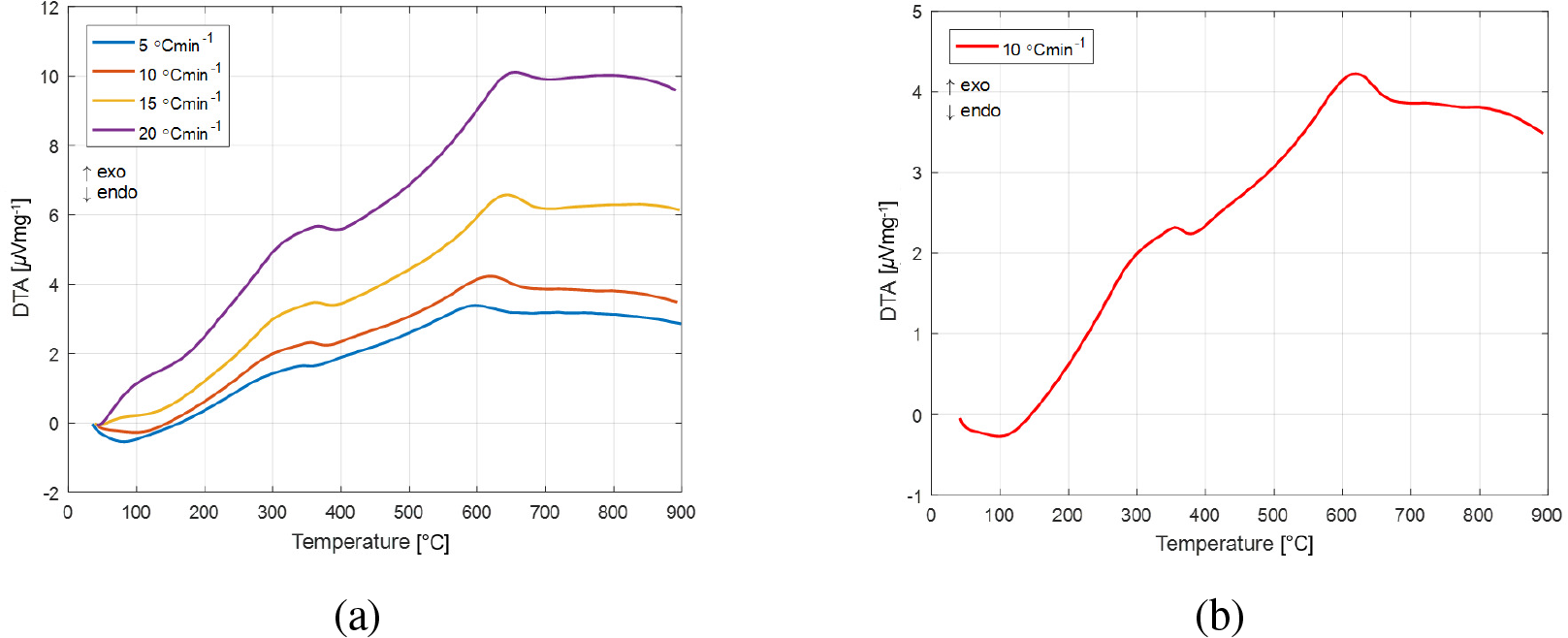
In the second phase, in the temperature range of 250-390/400 °C (Figure 3a-b), a broad exothermic DTA peak can be observed at all heating rates (where the largest mass loss of the sample occurs) and this can be attributed to the thermal decomposition of hemicelluloses and cellulose. The next exothermic peak can be observed in the temperature range of 580-680 °C, where its strict position depends on the applied heating rate (Figure 3a-b). This exothermic peak corresponds to the oxidation (by the oxygen from biomass material) of the complex, aromatic structure of the lignin. So, in the indicated temperature range, the decomposition and evaporation of pyrolyzable matter from lignin can be expected.
At the temperature of approximately 850 °C, the char was produced from each pyrolysis process monitoring, and produced char generally contains two entities. These entities are fixed carbon and ash. The summation of the fixed carbon and ash contents obtained for the apricot kernel shells (Table 1) is in very good agreement with the char yield that was obtained from every TG measurement (Figure 2a-d) (~ 16.45%). The values of char yield obtained at various operating temperatures and residence times can be obtained from the relation: Char yield , where is the mass at desired temperature and time, while mi is the mass at time t = 0 (min). Figure 4 shows the char yield of apricot kernel shell pyrolysis obtained at the different operating temperatures and different residence times (t1, t2, ..., t8) at the heating rate of β = 10 °C min-1.
The char yield of apricot kernel shell pyrolysis obtained at the different operating temperatures and different residence times at the heating rate of 10 °C min-1
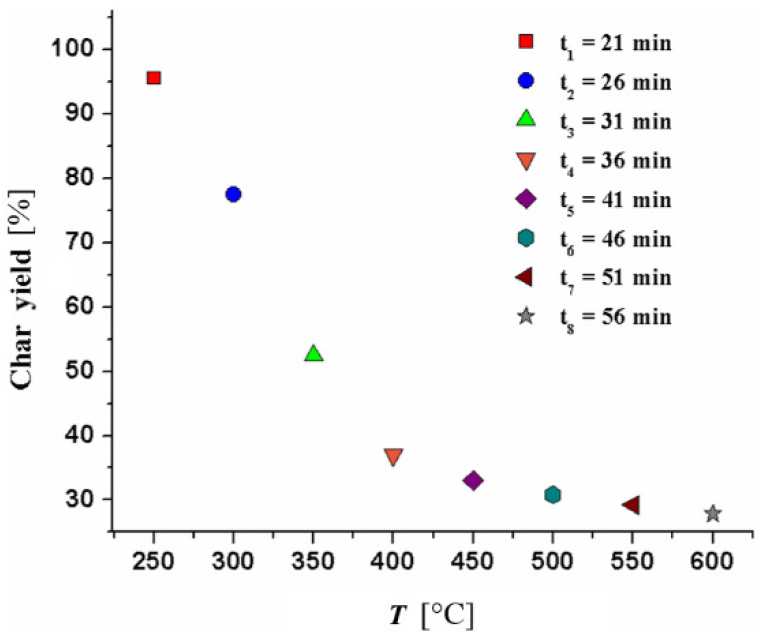
From obtained results, a very high yield of the char was obtained at lowest operating temperature and at shortest residence time [250 °C and t1 = 21 min. (~ 95.55%)], where with rise in the operating temperature and the prolongation of residence time, the char yields exponentially decrease and reach a minimum value at 600 °C for t8 = 56 min. (~ 27.83%). High char yields allow greater net CO2 benefits, but lower electrical output from slow pyrolysis. It can be observed from Figure 4 that a high char yield was obtained in the decomposition stage which occurs between 200 and 350 °C and can be related to the depolymerization reactions during cellulose decomposition. These reactions give rise to the oligomers and anhydrous sugars (levoglucosan, cellobiosan, cellotriosan, glucose, etc.). Above 350 °C, the random fragmentation of glucosidic bonds in cellulose, hemicellulose and their oligomers may generate volatile compounds with higher oxygen content, leaving a carbonaceous residue – the char. At temperatures above 400 °C, carbon monoxide (CO) and CO2 are released by the depolymerization reactions from lignin-rich aromatic carbonaceous matrix.
The global rate of biomass conversion depends on the chosen heating rate and, since the slow pyrolysis uses low heating rates, the whole process results in heat transfer rate limited biomass conversion. Although, the low heat transfer rates are not so critical for the process considering the long residence times used in the slow pyrolysis [39].
So, in the context of the actual discussion, it can be supposed that the tested biomass may contains a high lignin content which can produce high char yields, given the stability of lignin to the thermal decomposition, once it is preferentially converted to the solid char, instead of the liquids or the vapors. This assumption can also be validated from the shape appearance of the DTG curves in Figure 2a-d.
The two distinct mass loss rate peaks in DTG curves (shown in Figure 1) of apricot kernel shell pyrolysis significantly differentiated with other biomasses which show only one DTG peak (such as pine wood [40], bamboo [41], or corn stover [42]) or accompanied with extra “shoulder” peak, as in the case of wheat straw [43]. This might be caused by the higher content of lignin in the apricot kernel shells. Thus, the high levels of lignin in tested biomass can make the thermal decomposition of apricot kernel shell much slower than other biomasses, and lead to the mass loss of hemicelluloses and cellulose being separated more clearly (Figure 2).
Furthermore, the operating temperature represents the most important factor controlling the properties of resulting char (Figure 4). So, the yield of product decreases as operating temperature increases, as a result of greater thermal decomposition of organic constituents, while high yields obtained at lower operating temperatures are due to partially pyrolyzed biomass (Figure 4).
Namely, it happens due to more severe pyrolysis conditions which lead to an impact on energy distribution between three products of pyrolysis process, such as, gas, liquids, and solid. Namely, with an increasing of operating temperature, there is a tendency for the chemical energy to stay in liquids and gases, rather than in solids. According to Novak et al. [44], the decrease in the char yield with an increase in operating temperature is due to the dehydration of hydroxyl groups and thermal decomposition of cellulose and lignin structures with a great yield reduction which occurs above 400 °C (Figure 4). Therefore, the char obtained from lower operating temperatures, are characterized by higher volatile matter content with an easy decomposable material constituent [45], and, therefore, the amount of volatile matter in the char is supposed to be the highest with lowest operating temperature used in experiments [46].
Based on the estimated results for thermal conversion of apricot kernel shells, in order to obtain a high char yield, low temperature and as low heating rates as possible with long gas residence times are required.
To evaluate the variation of the apparent activation energy on the conversion degree during the major pyrolysis process, the forty-one levels of conversion α, varying from α = 0.10 (10%) to α = 0.90 (90%) with an increment of Δα = 0.02 (2%) employed at different heating rates (5, 10, 15 and 20 °C min-1) were used in the calculations.
Based on the applied isoconversional methods of the FR, KAS and OFW, in order to make a more accurate judgments about suitability and quality of fitting between given isoconversional methods, student’s test and D-W statistics were used in error analysis. Table 2 shows overall results of statistical analysis of regression lines obtained from FR, OFW, and KAS isoconversional methods, which are applied in kinetic analysis of pyrolysis.
The overall results of statistical analysis of isoconvversional regression lines obtained by FR, OFW and KAS methods, applied for the kinetic analysis of the apricot kernel shell pyrolysis process
| Method | R2 | Sum of dev. squares | Mean residual | Students’ coef. 95% | F-test | Durbin-Watson value | Durbin-Watson factor |
|---|---|---|---|---|---|---|---|
| FR | 0.98740 | 17,524.757 | 1.944 | 1.964 | ∞ | 0.267 | 3.806 |
| OFW | 1.00000 | 0.000 | 0.000 | 1.964 | NaN | NaN | NaN |
| KAS | 1.00000 | 0.000 | 0.000 | 1.964 | NaN | NaN | NaN |
D-W statistics tests the null hypothesis that the residuals from an ordinary least-squares regression are not auto-correlated against alternative that the residuals follow an AR(1) process [47]. From obtained D-W factor for FR method, the D-W factor towards 4.000 that indicates negative auto-correlation, while for OFW and KAS methods, the D-W factor is undefined (NaN) (Table 2).
In the case of FR method, the D-W factor suggests on the successive error terms which are negatively correlated. In regressions, this can imply an underestimation of the level of statistical significance. It can be noted that in a manner of a rule of thumb is that test statistic values in the range of 1.500 to 2.5000 are relatively normal. So, based on the established D-W factor for FR method, which is outside of this range, the results obtained from FR’s should be taken with great care [an indication associated with this fact is also a poor value for R2 (R2 = 0.98740) (Table 2)]. However, the D-W value close to zero, indicates that autocorrelation exists and supports the p-value tests, with high sum of residual squares.
On the other hand, the other two methods (OFW and KAS methods) are characterized by overall super-values of R2 (1.00000), with no sum of residual squares and mean residuals. From a statistical point of view, this means that the results obtained by applying these methods are exactly the same. This also indicates that there is no spread at all in obtained results data, and also, it can be extracted only one (single) value with a high probability which would constitute the mean value from a whole data sample. Distribution of the Ea values in a function of α, estimated by the FR, KAS and OFW methods for apricot kernel shell pyrolysis was presented in Figure 5a-c.
Effective activation energy estimated from the KAS and OFW methods showed excellent agreement with each other, which was confirmed by the results given in Table 2. However, there are some differences in the obtained Ea values calculated from the KAS and OFW methods, with those calculated from the FR method.
This can be clearly seen from the calculated mean values of effective activation energy, which are as follows: Ea,meanFR [kJ mol-1] = 229.68, Ea,meanKAS [kJ mol-1] = 221.42, and Ea,meanOFW [kj mol-1] = 220.02, respectively. It can be seen that Ea,meanFR ≠ Ea,meanKAS ≈ Ea,meanOFW, so that actual difference in Ea,mean values between differential and integral isoconversional methods suggests on the presence of reaction complexity of the process under study, which can also be seen from the shape of Ea-α dependency (Figure 5). However, consistency of results from both integral methods, and measured TGA curves from multi-heating rate scanning, validated accuracy and reliability of estimated effective activation energy.
Variation of Ea with respect to conversion degree (α) estimated by the FR, KAS and OFW, respectively, for the apricot kernel shell pyrolysis (a-c)
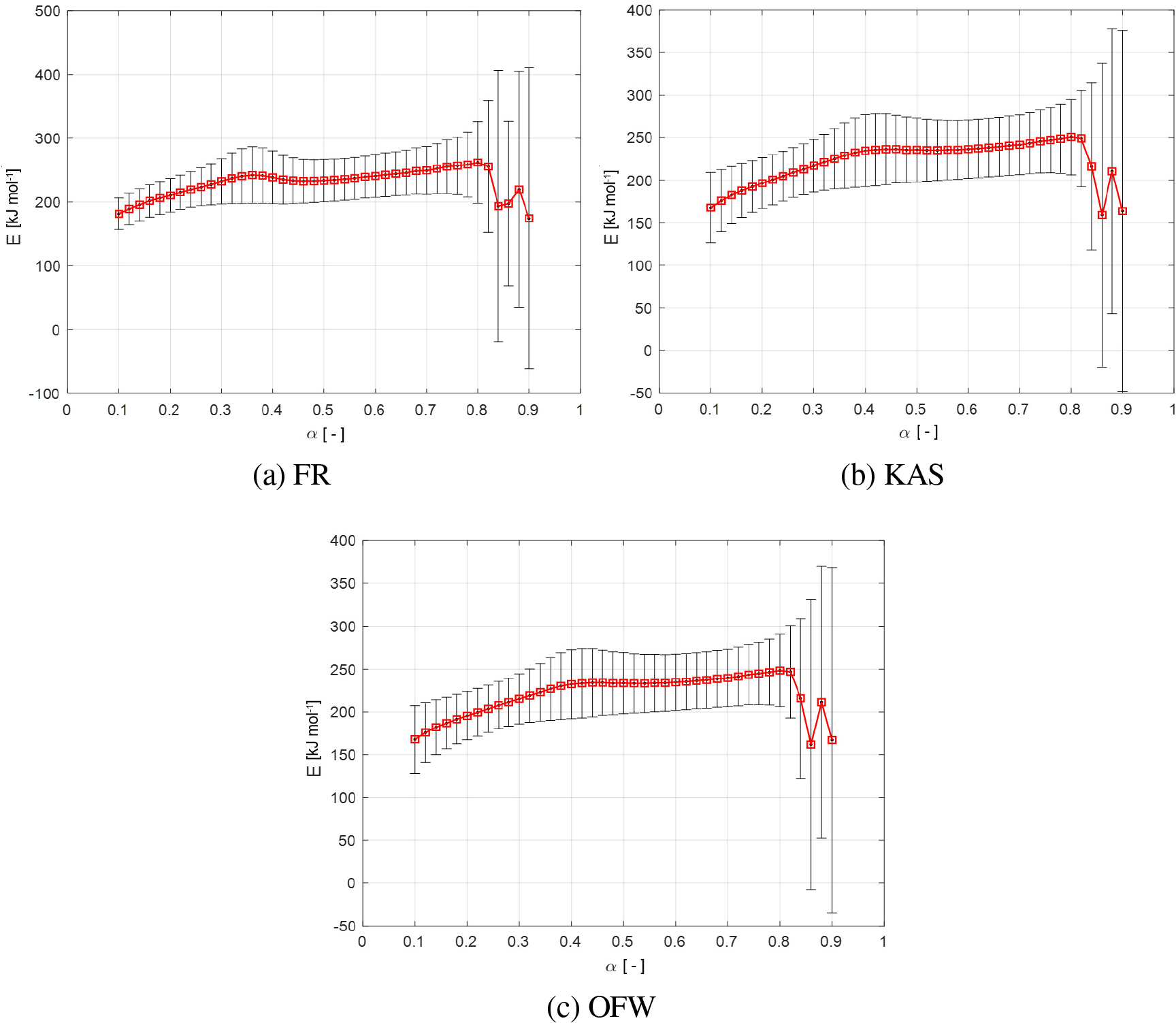
The value of Ea was affected by several factors, such as different kinetic models, heating rate, species of the biomass, the particle size, and different types of the used TGA (modulated, quasistatic, etc.). Thus, the obtained effective activation energy of apricot kernel shell pyrolysis was only valid for this kind of the experimental parameters described in sub-sections 2.1, and 2.3.
It can be observed from Figure 6 that certain fluctuations of Ea-α dependence exist, and this revealed that apricot kernel shell pyrolysis was a complex process [48], which may include parallel, competitive and consecutive reaction pathways [49].
The first process area, from α = 0.10 to α = 0.40 (Figure 5b and 5c), the Ea value increases from 168.0 to 235.0 kJ mol-1 for the KAS method, and from 168.0 to 232.0 kJ mol-1 for the OFW method, as conversion degree increased, and this could be mainly attributed to hemicelluloses decomposition. In the initial stage, the decomposition started easily on weakly linked sites inherent to the polymeric lineal chain of the hemicelluloses, which led to the lower effective activation energy. After the weaker bonds broke, the random scission on the lineal chain can be expected, which may cause the increase in Ea. Meanwhile, it can be expected that there is an interaction between hemicelluloses and lignin [50], where the obtained value of Ea in the actual stage is much higher than the value for the single component of xylan (represents the hemicelluloses) usually analyzed in pyrolysis process (87.65 kJ mol-1 and 69.39 kJ mol-1) [51].
The second process area, which encompass 0.40 < α < 0.80, shows that there are some stabilized values in Ea, observing all three isoconversional methods (Figure 5a and Figure 5c), with average values of and . The indicated conversion range falls in the experimental temperature range of ΔT = 310-360 °C, and this area was just located between two mass loss rate peaks in DTG curves (Figure 2a and Figure 2d). Since that we assumed a presence of high lignin content in the tested biomass, this issue may leads to a tighter cross-link of three pseudo-components in the apricot kernel shell. On the other hand, for cellulose decomposition in this reaction stage, the cellulose initially pyrolyzed to active cellulose according to Briodo-Shafizadeh extended model, and this can lead to reducing of the degree of polymerization and the length of molecule chain. The active cellulose represents the intermediate product before further pyrolysis. This fact was validated from a certain increase of Ea value during transition from the first to the second reaction stage. In considered α range (0.40 < α < 0.80), the active cellulose continues to decompose with approximately constant effective activation energy. This decomposition process may eventually split into two parallel and competitive reaction pathways, one which produces char favored at lower temperatures, and the other that produces tar and gas occurring prior to higher temperatures [52]. The obtained value of Ea for this stage is higher than the single (or pure) component of cellulose (119.21 kJ mol-1 [50] and 150-175 kJ mol-1 [53]).
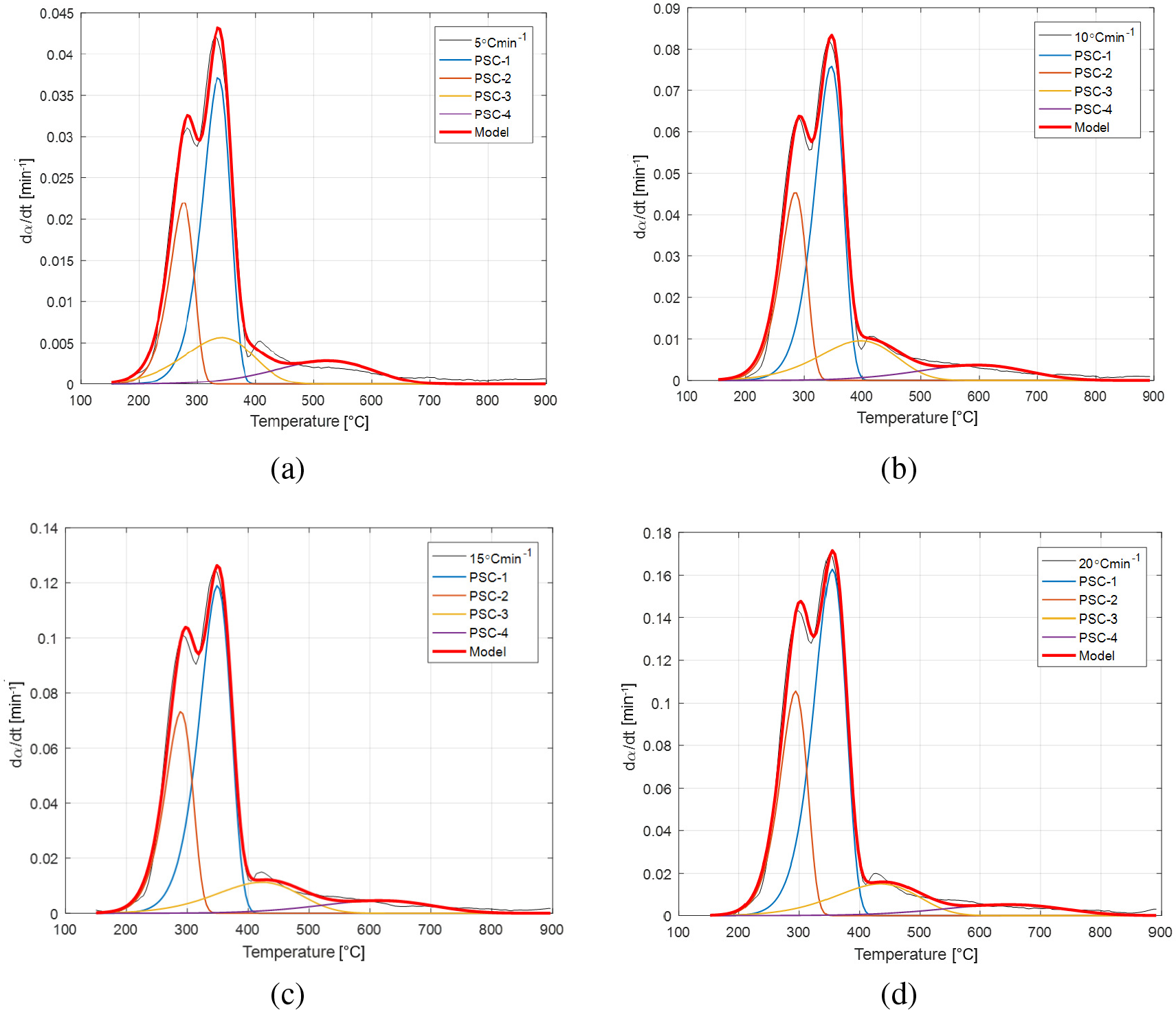
The experimental and model pyrolysis rate curves for 4 pseudo-components model (PSC-1, PSC-2, PSC-3 and PSC-4) at different heating rates (a-d)
In the final process area, for α > 0.80 (Figure 5), the significant variation in Ea value with decreased trends can be observed. In this area, the Ea value drops at 158.0 kJ mol-1 (for KAS method) and at 161.8 kJ mol-1 (for OFW method), and actual behavior can be related to lignin decomposition. Since that lignin is mainly composed of three kinds of benzene-propane, which was heavily cross-linked, these facts cause it to have a very high thermal stability. In the later stage of pyrolysis process, within the high temperature zone, part of three-dimensional network structure broke, which requires a much higher Ea values. A large amount of solid product with lower reaction activities may be formed in this process area, which can lead to increased Ea’s. This fact explains why the obtained Ea value in an actual stage (see above) is much higher than Ea value for the pure alkali lignin (70.68 kJ mol-1 [50]).
It can be noted that the identified variation of Ea with α in the conversion degrees range of 0.10 ≤ α ≤ 0.80 was typical for biomass feedstock with a high content of lignin with application of KAS and OFW methods, as is the case with apricot kernel shells (the apricot kernel shell lignocellulosic content reported by Demirbas [54]: cellulose = 22.4%, hemicelluloses = 20.8%, and lignin = 51.4%). Consequently, the interaction of biomass pseudo-components with various contents and structures may leads to distribution variations in Ea values.
Using the algorithm described in the methodology section, the simulation was performed between 3 and 5 pseudo-components, but the best fit quality results show the data related to four pseudo-components model. Also, the proposed kinetic model includes composition analysis with already presented methodology [30].
Simulations for four pseudo-components (designated by PSC-1, PSC-2, PSC-3 and PSC-4) with corresponding model fit parameters at different heating rates, together with overall model values are presented in Table 3 and Figure 6a-d. Optimization strategy includes the use of Akaike Information Criterion (AIC) for statistical identification of the number of distinct processes and this criterion has already been included in the algorithm described in sub-section 3.1. Among all pseudo-component models (with three, four and five ‒ components), the four pseudo-component model showed the lowest values of statistical parameters and modeling quality parameters, in the case of the best assessment of model accuracy. Therefore, the lowest Quality of Fit (QOF) values and extremely low values of AIC for maximum number of pseudo-components which were used without disturbing the fit quality at all heating rates were obtained for 4-pseudo-component model (Table 3).
In accordance with necessary and sufficient conditions for the minimum number of processes taking place during pyrolysis, the AIC values (Table 3) clearly show that (excluding dehydration process) there are four unique processes which occur in the decomposition of apricot kernel shell, and these correspond to cellulose (PSC-1), hemicelluloses (PSC-2), lignin (PSC-3) decompositions, as well as the char combustion (PSC-4) (oxidation) process, respectively.
Within active pyrolysis region, the decomposition of PSC-1 and PSC-2 occurs (cellulose and hemicelluloses) in the temperature range of 150-400 °C (Figure 6a-d). On the other hand, the decomposition of PSC-3 which corresponds to lignin takes place in both, active and passive pyrolysis regions (Figure 6a-d), indicating a very broad decomposition temperature range. In addition, PSC-4 processing occurs only in the passive pyrolysis region (Figure 6a-d).
Considering results presented in Table 3, it can be observed that contribution φ of PSC-1, PSC-2 and PSC-3 in the overall apricot kernel shell pyrolysis at all heating rates is approximately identical, while the contribution of PSC-4 is significantly lower. Generally, in biomass lignocellulose breakdown, the identified PSC-1, PSC-2 and PSC-3 pseudo-components which correspond to the cellulose, hemicelluloses and lignin, respectively, are within active pyrolysis and passive pyrolysis regions.
Observing different heating rates, and taking the average values of the apparent activation energy for the model, the Ea follows an order: PSC-3 (pseudo-lignin) (55.2 kJ mol-1) < PSC-2 (pseudo-hemicelluloses) (119.9 kJ mol-1) < PSC-1 (pseudo-cellulose) (123.1 kJ mol-1). Since that Ea represents the minimum energy required to start a reaction, the lowest value of Ea for PSC-3 (pseudo-lignin) indicates that this pseudo-component decomposes easier than the other two pseudo-components. It should be noted that thermal decomposition of lignin is generally influenced by the heat and mass transfer processes, which significantly affect the apparent activation energy and pre-exponential factor values. The obtained values of Ea for PSC-3 that correspond to lignin decomposition (Table 3, with an average value of 55.2 kJ mol-1) and for average reaction order of n = 1.19 (Table 3) is typical for isolated lignin decomposition [55] (through the first-order or close to the first-order reactions, with an Ea varying from 54.3 kJ mol-1 to 81.2 kJ mol-1 covering a very broad temperature range of 200-1,167 °C, with pre-exponential factor A varying from × 100.3 to × 103 min-1 [56]). The PSC-4 pseudo-component instantly arises from PSC-3 decomposition reaction, since that lignin may decompose through two reaction pathways one of which occurs with the lower Ea (liberating H2O, CO2, CO and char producing), while others occur with the higher Ea (producing monomers). The cleavage of the functional groups gives low molecular weight products, while the complete re-arrangement of the lignin molecule backbone at higher temperatures leads to 30-50 wt% of char and to the release of volatile products. The cleavage of the aryl-ether linkages results in the formation of highly reactive and unstable free radicals that may further react through re-arrangement, electron abstraction or radical-radical interactions, to form products with increased stability. The PSC-4 accounts for the enriched product with char compound that obeys oxidation reaction, which characterizes with elevated average Ea value (59.6 kJ mol-1, Table 3) and with higher average reaction order (n = 1.22, Table 3). This reaction takes place at much higher temperature zone of the apricot kernel shell pyrolysis, where char oxidation may occur when oxygen reaches the char particle surface during devolatilization stage [57]. This can especially be expressed for the biomass feedstock that contains a high oxygen concentration in its composition, as is the case for apricot kernel shells (Table 1). The char oxidation occurs at high temperatures and was followed by highly exothermic effect (typically for oxidative surface reactions) where for apricot kernel shell pyrolysis it can be expected about/or above 600 °C (Figure 2a-d). This process is characterized with a slow rate (Figure 6a-d), so, the completion of char oxidation requires more residence time, than dehydration, and devolatilization processes. This process is also strongly governed by the particle sizes of the used biomass, and the rate is higher for a smaller particles, and similar to devolatilization, the elevated temperature can significantly accelerates the actual process [58].
For PSC-1 and PSC-2 decompositions related to cellulose and hemicelluloses decomposition reactions, the obtained apparent activation energies (Table 3) are lower than those for pure cellulose (between 140.00 and 240.23 kJ mol-1) [59] and pure hemicelluloses (xylan) (179.84 kJ mol-1) [60]. This difference may be due to the temperature difference of various reaction stages, which can vary from one to another biomass feedstock used in pyrolysis experiments. Also, the lignocellulose content may affect this behavior, since that lignin could have an impact on the required energy to decompose cellulose and hemicelluloses. These variations can also be seen from the obtained FWHM’s attached to corresponding decomposition rate curves of individual pseudo-components (Table 3), which also shows significant changes in its values. From results presented in Table 3, it can be seen that in both cases, for PSC-1 and PSC-2 decompositions, non-integer reaction orders were obtained. These values are characteristic for the description of random scission mechanisms, where the non-integer reaction orders indicate that the processes are complex and comprise several elementary reaction stages. So, this behavior is not unusual considering that both, cellulose and hemicelluloses degradation includes a series of decomposition reaction pathways which cannot be described by the simple integer reaction-order kinetics, because the complicated reactions related to entire apricot kernel shell pyrolysis. On the other hand, in all considered cases, it can be observed that the kinetic parameters (Ea and A) calculated by the Janković et al. [30], are in good agreement with those derived from the model (Table 3). On the other hand, the pseudo-component fraction X related to each component varies slightly with the change of the heating rate (Table 3), and theoretically calculated pseudo-component fraction values are arranged in the following order: PSC-4 < PSC-3 < PSC-2 < PSC-1. These fractions follow the total area values under the each rate decomposition curve attached to individual PSC (Table 3). This behavior can indicate on contribution of individual components to the overall TGA profile for apricot kernel shell pyrolysis (Figure 2a-d). Namely, from these results, it can be seen that the contribution of cellulose dominates, which is confirmed by the results established through the MS analysis (Figure 4).
Kinetic parameters of the model and quality of fit results for each pseudo-component in the case of apricot kernel shell pyrolysis process at the different heating rates
| Pseudo-component | 5 °C min−1 | ||||||||
| φ | A [min−1] | Ea [kJ mol−1] | n | X [%] | A [min−1] | Ea [kJ mol−1] | FWHMa | Tot. areab | |
| PSC-1 | 0.2983 | 9.995 × 109 | 128.5 | 1.51 | 44.82 | 1.945 × 1011 | 138.8 | 52.08 | 2.2826 |
| PSC-2 | 0.2984 | 9.996 × 109 | 118.3 | 1.27 | 24.28 | 1.596 × 1011 | 124.6 | 47.74 | 1.1975 |
| PSC-3 | 0.2984 | 1.876 × 102 | 48.6 | 1.19 | 18.12 | 2.936 × 103 | 53.6 | 138.87 | 0.8415 |
| PSC-4 | 0.1049 | 1.169 × 102 | 57.5 | 1.38 | 12.78 | 8.713 × 102 | 63.3 | 195.29 | 0.5939 |
| QOFc | 1.7359 | ||||||||
| AICd | −2,385.47 | ||||||||
| Pseudo-component | 10 °C min−1 | ||||||||
| φ | A [min−1] | Ea [kJ mol−1] | n | X [%] | A [min−1] | Ea [kJ mol−1] | FWHMa | Tot. areab | |
| PSC-1 | 0.2992 | 9.998 × 109 | 116.8 | 1.29 | 48.99 | 9.193 × 1010 | 134.6 | 55.92 | 4.8616 |
| PSC-2 | 0.2991 | 9.998 × 109 | 126.8 | 1.55 | 24.79 | 6.251 × 1011 | 129.7 | 47.32 | 2.5955 |
| PSC-3 | 0.2990 | 1.266 × 102 | 61.2 | 1.28 | 17.06 | 4.146 × 103 | 57.0 | 154.86 | 1.6031 |
| PSC-4 | 0.1027 | 2.47 × 102 | 51.5 | 1.18 | 9.17 | 1.493 × 103 | 68.8 | 215.09 | 0.8655 |
| QOFc | 1.4458 | ||||||||
| AICd | −2,190.48 | ||||||||
| Pseudo-component | 15 °C min−1 | ||||||||
| φ | A [min−1] | Ea [kJ mol−1] | n | X [%] | A [min−1] | Ea [kJ mol−1] | FWHMa | Tot. areab | |
| PSC-1 | 0.2311 | 9.259 × 109 | 123.6 | 1.75 | 53.42 | 2.010 × 1010 | 125.4 | 60.37 | 7.9550 |
| PSC-2 | 0.2990 | 1.134 × 1010 | 116.4 | 1.30 | 25.84 | 9.544 × 1011 | 130.1 | 47.43 | 4.2967 |
| PSC-3 | 0.2993 | 3.117 × 102 | 53.8 | 1.15 | 13.36 | 6.334 × 103 | 59.3 | 159.54 | 1.9728 |
| PSC-4 | 0.1706 | 1.285 × 102 | 64.8 | 1.14 | 7.38 | 2.709 × 103 | 71.8 | 215.60 | 1.0723 |
| QOFc | 1.3697 | ||||||||
| AICd | −2,065.94 | ||||||||
| Pseudo component | 20 °C min−1 | ||||||||
| φ | A [min−1] | Ea [kJ mol−1] | n | X [%] | A [min−1] | Ea [kJ mol−1] | FWHMa | Tot. areab | |
| PSC-1 | 0.2704 | 8.435 × 109 | 123.5 | 1.65 | 52.10 | 3.706 × 1010 | 128.2 | 60.12 | 11.1290 |
| PSC-2 | 0.2957 | 1.765 × 1010 | 118.0 | 1.31 | 28.91 | 1.666 × 1011 | 122.3 | 51.53 | 6.2072 |
| PSC-3 | 0.2983 | 6.003 × 102 | 57.0 | 1.14 | 12.70 | 1.087 × 104 | 62.0 | 158.88 | 2.6118 |
| PSC-4 | 0.1356 | 1.327 × 102 | 64.5 | 1.16 | 6.29 | 2.805 × 103 | 72.7 | 227.58 | 1.3017 |
| QOFc | 1.2675 | ||||||||
| AICd | −1,969.24 | ||||||||
Full width at half maximum for each pseudo-component rate curve
Total area under the each pseudo-component rate curve
The quality of fits
AIC was used to indicate the model performance
The deconvolution of apricot kernel shell through the STA using the multicomponent model, expresses the devolatilization kinetics of tested biomass feedstock, as the individual components. The total Ea of individual reactions should be correlated with devolatilization Ea values obtained from isoconversional (“model-free”) approach. Considering all heating rates, the total Ea value related to three main pseudo-components of biomass (pseudo-cellulose, pseudo-hemicelluloses and pseudo-lignin) is equal to which is slightly higher than mean values of effective activation energy, obtained by “model-free” methods. However, the observed difference is still within acceptable limit.
Slow pyrolysis and multicomponent kinetic properties of apricot kernel shells were examined. Kinetic parameters of pyrolysis process were estimated using the 4-pseudo-component models, together with applied isoconversional approaches (FR, KAS and OFW). The multicomponent kinetic model has successfully executed the deconvolution of pyrolysis rate curves at various heating rates, where four pseudo-components, PSC-1, PSC-2, PSC-3 and PSC-4 were recognizable for cellulose, hemicelluloses, and lignin decomposition processes, as well as oxidation reaction. It was found that theoretically calculated pseudo-component fraction X varies slightly with heating rate, where its values are grouped in relation to a given pseudo-components in a following order: PSC-4 < PSC-3 < PSC-2 < PSC-1. It was established that results indicate on contribution of individual components to the overall TGA profile for apricot kernel shell pyrolysis. This showed that contribution of cellulose decomposition reactions dominates through entire process. The pseudo kinetic compensation effect was identified for the slow pyrolysis of apricot kernel shells. From this phenomenon, it was found that hemicelluloses bond rupturing is located between cellulose and lignin bonds rupturing. In the case of char combustion process, the high variation of Ea with α was identified. Conclusions drawn from this study can be important guidelines for future investigations of pyrolysis properties of waste lignocellulosic biomass feedstock.
Authors would like to acknowledge financial support of Ministry of Education, Science and Technological Development of the Republic of Serbia under the Projects III42010, 172015 and III45005.
- , , Advances in Solar Energy, 1982
- ,
Techno-economic Assessment of Integrated Hydrothermal Liquefaction and Combined Heat and Power Production from Lignocellulose Residues ,J. Sustain. Dev. Energy Water Environ. Syst , Vol. 6 (1),pp 89-113 , 2018, https://doi.org/https://doi.org/10.13044/j.sdewes.d5.0177 - ,
Comparison of Slow and Fast Pyrolysis for Converting Biomass into Fuel ,Renew. Energy , Vol. 124 ,pp 197-201 , 2018, https://doi.org/https://doi.org/10.1016/j.renene.2017.04.060 - ,
Pyrolysis of Waste Biomass: Investigation of Fast Pyrolysis and Slow Pyrolysis Process Conditions on Product Yield and Gas Composition ,J. Energy Inst , Vol. 86 (4),pp 233-241 , 2013, https://doi.org/https://doi.org/10.1179/1743967113Z.00000000067 - ,
Modeling and Simulation of Combustion Processes Pf Charring and Non-Charring Solid Fuels ,Prog. Energy Combust. Sci , Vol. 19 (1),pp 71-104 , 1993, https://doi.org/https://doi.org/10.1016/0360-1285(93)90022-7 - , , Research in Thermochemical Biomass Conversion, 1988
- ,
The Art, Science and Technology of Charcoal Production ,Ind. Eng. Chem. Res , Vol. 42 (8),pp 1619-1640 , 2003, https://doi.org/https://doi.org/10.1021/ie0207919 - ,
Pyrolysis of Wood/Biomass for Bio-Oil: A Critical Review ,Energy Fuels , Vol. 20 (3),pp 848-889 , 2006, https://doi.org/https://doi.org/10.1021/ef0502397 - ,
Agroindustrial Waste for Lead and Chromium Biosorption ,J. Sustain. Dev. Energy Water Environ. Syst , Vol. 6 (2),pp 341-350 , 2018, https://doi.org/https://doi.org/10.13044/j.sdewes.d5.0184 - ,
Pyrolysis of Apricot Kernel Shell in a Fixed-Bed Reactor: Characterization of Bio-Oil and Char ,J. Anal. Appl. Pyrol , Vol. 107 ,pp 17-24 , 2014, https://doi.org/https://doi.org/10.1016/j.jaap.2014.01.019 - ,
Adsorption of Malachite Green (MG) onto Apricot Stone Activated Carbon (ASAC) - Equilibrium, Kinetic and Thermodynamic Studies ,J. Mater. Process. Environ , Vol. 5 (1),pp 1-10 , 2017 - ,
Preparation and Characterization of Activated Carbons by One-Step Steam Pyrolysis/Activation from Apricot Stones ,Microporous Mesoporous Mater , Vol. 88 (1-3),pp 126-134 , 2006, https://doi.org/https://doi.org/10.1016/j.micromeso.2005.09.003 - ,
Potential of Biofuel Production from Pistachio Waste in Iran ,Renew. Sustain. Energy Rev. , Vol. 72 ,pp 510-522 , 2017, https://doi.org/https://doi.org/10.1016/j.rser.2017.01.111 - ,
Kinetics of Thermal Degradation of Char-Forming Plastics from Thermogravimetry- Application to a Phenolic Resin ,J. Polym. Sci. Part C: Polym. Symp , Vol. 6 (1),pp 183-195 , 1964, https://doi.org/https://doi.org/10.1002/polc.5070060121 - ,
The Universality of Friedman's Isoconversional Analysis Results in a Model-Less Prediction of Thermodegradation Profiles ,Thermochim. Acta , Vol. 650 ,pp 1-7 , 2017, https://doi.org/https://doi.org/10.1016/j.tca.2017.01.011 - ,
Reactions Kinetics in Differential Thermal Analysis ,Anal. Chem , Vol. 29 (11),pp 1702-1706 , 1957, https://doi.org/https://doi.org/10.1021/ac60131a045 - ,
Method of Determining Activation Deterioration Constant of Electrical Insulating Materials ,Res. Rep. Chiba. Inst. Technol. (Sci. Technol.) , Vol. 16 ,pp 22-31 , 1971, https://doi.org/https://doi.org/10.7209/tanso.1971.22 - ,
A New Method of Analyzing Thermogravimetric Data ,Bull. Chem. Soc. Jpn , Vol. 38 (11),pp 1881-1886 , 1965, https://doi.org/https://doi.org/10.1246/bcsj.38.1881 - ,
A Quick, Direct Method for the Determination of Activation Energy from Thermogravimetric Data ,J. Polym. Sci. Part B: Polym. Lett , Vol. 4 (51),pp 323-328 , 1966, https://doi.org/https://doi.org/10.1002/pol.1966.110040504 - ,
Thermogravimetric Kinetic Study of Agricultural Residue Biomass Pyrolysis Based on Combined Kinetics ,Bioresour. Technol , Vol. 219 ,pp 510-520 , 2016, https://doi.org/https://doi.org/10.1016/j.biortech.2016.07.136 - , , 2017
- , , 2015
- ,
Solid-State Kinetic Models: Basics and Mathematical Fundamentals ,J. Phys. Chem. B , Vol. 110 (35),pp 17315-17328 , 2006, https://doi.org/https://doi.org/10.1021/jp062746a - ,
Isoconversional Kinetic Analysis of Olive Pomace Decomposition Under Torrefaction Operating Conditions ,Fuel Process. Technol , Vol. 130 ,pp 147-154 , 2015, https://doi.org/https://doi.org/10.1016/j.fuproc.2014.09.043 - ,
Series Approximations to Equation of Thermogravimetric Data ,Nature , Vol. 207 ,pp 290-291 , 1965, https://doi.org/https://doi.org/10.1038/207290a0 - ,
Multicomponent Devolatilization Kinetics and Thermal Conversion of Imperata Cylindrica ,Applied Thermal Engineering , Vol. 105 ,pp 931-940 , 2016, https://doi.org/https://doi.org/10.1016/j.applthermaleng.2016.04.165 - ,
Modeling the Pyrolysis of Biomass Particles: Studies on Kinetics, Thermal and Heat Transfer Effects ,Can. J. Chem. Eng , Vol. 69 (4),pp 907-915 , 1991, https://doi.org/https://doi.org/10.1002/cjce.5450690413 - ,
Evaluation of Wood Residues From Crete as Alternative Fuels ,Int. J. Energy Environ , Vol. 1 ,pp 667-674 , 2010 - ,
Characterization Analysis of Poplar Fluff Pyrolysis Products. Multi-component Kinetic Study ,Fuel , Vol. 238 ,pp 111-128 , 2019, https://doi.org/https://doi.org/10.1016/j.fuel.2018.10.064 - ,
TSA-MS Characterization and Kinetic Study of the Pyrolysis Process of Various Types of Biomass Based on the Gaussian Multi-Peak Fitting and Peak-To-Peak Approaches ,Fuel , Vol. 234 ,pp 447-463 , 2018, https://doi.org/https://doi.org/10.1016/j.fuel.2018.07.051 - ,
Prediction of Calorific Value of Biomass from Proximate Analysis ,Energy Proc , Vol. 107 ,pp 130-136 , 2017, https://doi.org/https://doi.org/10.1016/j.egypro.2016.12.149 - ,
Preliminary Results on the Ash Behavior of Peach Stones During Fluidized Bed Gasification: Evaluation of Fractionation and Leaching as Pre-Treatments ,Biomass and Bioenergy , Vol. 28 (3),pp 331-338 , 2005, https://doi.org/https://doi.org/10.1016/j.biombioe.2004.08.016 - ,
The Energy Potentials of Some Agricultural Wastes as Local Fuel Materials in Nigeria ,CIGR E-Journal , Vol. VII ,pp 1-10 , 2005 - ,
Combustion of a Pb (II)-Loaded Olive Tree Pruning Used as Biosorbent ,J. Hazard. Mater , Vol. 308 ,pp 285-293 , 2016, https://doi.org/https://doi.org/10.1016/j.jhazmat.2016.01.045 - ,
Characteristics of Hemicellulose, Cellulose and Lignin Pyrolysis ,Fuel , Vol. 86 (12-13),pp 1781-1788 , 2007, https://doi.org/https://doi.org/10.1016/j.fuel.2006.12.013 - ,
Kinetic Study of Wood Chips Decomposition by TGA ,Chem. Pap , Vol. 64 (2),pp 174-181 , 2010, https://doi.org/https://doi.org/10.2478/s11696-009-0109-4 - ,
Thermo-Kinetics Study of Orange Peel in Air ,J. Therm. Anal. Calorim , Vol. 98 (1),pp 309-315 , 2009, https://doi.org/https://doi.org/10.1007/s10973-009-0146-9 - ,
Kinetic Study of the Thermal Decomposition of Hemicellulose Isolated from Corn Stalk ,BioRes , Vol. 5 (2),pp 1281-1291 , 2010 - ,
Towards a Carbon-Negative Sustainable Bio-Based Economy ,Front. Plant. Sci , Vol. 4 ,pp 1-17 , 2013, https://doi.org/https://doi.org/10.3389/fpls.2013.00174 - ,
Pyrolysis of Poplar Wood Sawdust by TGA-FTIR and Py-GC/MS ,J. Anal. Appl. Pyrol , Vol. 102 ,pp 16-231 , 2013, https://doi.org/https://doi.org/10.1016/j.jaap.2013.04.009 - ,
The Pyrolysis Characteristics of Moso Bamboo ,J. Anal. Appl. Pyrol , Vol. 94 ,pp 48-52 , 2012, https://doi.org/https://doi.org/10.1016/j.jaap.2011.10.010 - ,
Thermogravimetric Characterization of Corn Stover as Gasification and Pyrolysis Feedstock ,Biomass and Bioenergy , Vol. 32 (5),pp 460-467 , 2008, https://doi.org/https://doi.org/10.1016/j.biombioe.2007.11.004 - ,
In-Depth Investigation on the Pyrolysis Kinetics of Raw Biomass. Part I: Kinetic Analysis for the Drying and Devolatilization Stages ,Bioresour. Technol , Vol. 131 ,pp 40-46 , 2013, https://doi.org/https://doi.org/10.1016/j.biortech.2012.12.136 - ,
Impact of Biochar Amendment on Fertility of a Southeastern Coastal Plain Soil ,Soil Sci , Vol. 174 (2),pp 105-112 , 2009, https://doi.org/https://doi.org/10.1097/SS.0b013e3181981d9a - ,
Physical and Chemical Characterization of Biochars Derived from Different Agricultural Residues ,Biogeosci , Vol. 11 ,pp 6613-6621 , 2014, https://doi.org/https://doi.org/10.5194/bg-11-6613-2014 - ,
Effects of Chemical Inhomogeneity on Pyrolysis Behaviors of Corn Stalk Fractions ,Fuel , Vol. 129 ,pp 111-115 , 2014, https://doi.org/https://doi.org/10.1016/j.fuel.2014.03.061 - , , Handbook of Regression Analysis, 2013
- ,
Kinetic Modeling of the Pyrolysis of Biomass and Biomass Components ,Can. J. Chem. Eng , Vol. 67 (1),pp 75-84 , 1989, https://doi.org/https://doi.org/10.1002/cjce.5450670111 - ,
How to Determine Consistent Biomass Pyrolysis Kinetics in a Parallel Reaction Scheme ,Fuel , Vol. 123 ,pp 230-240 , 2014, https://doi.org/https://doi.org/10.1016/j.fuel.2014.01.014 - ,
Characterization of Switchgrass, Cellulose, Hemicellulose and Lignin for Thermochemical Conversions ,J. Biobased Mater. Bioenergy , Vol. 6 (3),pp 249-258 , 2012, https://doi.org/https://doi.org/10.1166/jbmb.2012.1216 - ,
Thermogravimetric-Analysis-Fourier Transform Infrared Analysis of Palm Oil Waste Pyrolysis ,Energy Fuels , Vol. 18 (6),pp 1814-1821 , 2004, https://doi.org/https://doi.org/10.1021/ef030193m - ,
Char Yield on Pyrolysis of Cellulose ,Combustion and Flame , Vol. 24 ,pp 263-268 , 1975, https://doi.org/https://doi.org/10.1016/0010-2180(75)90156-X - ,
Kinetic Analysis of Co-Pyrolysis of Cellulose and Polypropylene ,J. Therm. Anal. Calorim , Vol. 117 (3),pp 1441-1451 , 2014, https://doi.org/https://doi.org/10.1007/s10973-014-3866-4 - , , Series: Green Energy and Technology, 2010
- ,
Product Compositions and Kinetics in the Rapid Pyrolysis of Sweet Gum Hardwood ,Ind. Eng. Chem. Process Des. Dev , Vol. 24 (3),pp 836-844 , 1985, https://doi.org/https://doi.org/10.1021/i200030a053 - ,
Thermal Degradation of Lignin � A Review ,Cellul. Chem. Technol , Vol. 44 (9),pp 353-363 , 2010 - ,
Simultaneous Pyrolysis and Char Combustion ,Fuel , Vol. 72 (5),pp 599-609 , 1993, https://doi.org/https://doi.org/10.1016/0016-2361(93)90571-I - ,
Characterization of Biomass Combustion at High Temperatures Based on an Upgraded Single Particle Model ,Appl. Energy , Vol. 156 ,pp 749-755 , 2015, https://doi.org/https://doi.org/10.1016/j.apenergy.2015.04.027 - ,
Thermogravimetric Kinetics of Lignocellulosic Biomass Slow Pyrolysis Using Distributed Activation Energy Model, Fraser-Suzuki Deconvolution, and Iso-Conversional Method ,Energy Convers. Manag , Vol. 118 ,pp 1-11 , 2016, https://doi.org/https://doi.org/10.1016/j.enconman.2016.03.058 - ,
A Novel Gaussian-DAEM-Reaction Model for the Pyrolysis of Cellulose, Hemicellulose and Lignin ,RSC Adv , Vol. 4 (34),pp 17513-17520 , 2014, https://doi.org/https://doi.org/10.1039/c4ra01445f




