Integration of renewable energy production and storage technologies to District Heating (DH) systems is a widely researched area. Heat Pumps (HPs) have been recognized as a key technology for increasing the share of renewables in DH systems and within the heating sector in general. In Ritchie [1], the possibilities the placement, connection and operational principles of HPs are carefully examined. The emphasis on country-specific or European level studies is often in large-scale HPs, e.g., in Kontu et al. [2] for Finland and in David et al. [3] for Europe.
In this paper, the focus is on distributed HPs in a specific residential area, one option identified in Ritchie [1]. The HPs are located within the buildings or operate as a shared heat supply for the residential area. Geothermal energy or exhaust air is utilised as heat sources. The motivation for the approach is that while the large-scale HPs have been identified as an attractive option for heat supply, the heat sources in the required scale are not always available. The analysis is completed by adding the option of having Solar Collectors (SCs) or Photovoltaic (PV) panels installed on building rooftops. Building and area-level heat storages are also considered. The method used is capacity optimisation using a Mixed-integer Linear Programming (MILP) optimisation model.
In Olsthoorn et al. [4], recent advancements of modelling and optimisation of energy production in DH systems are reviewed in detail. These studies concern mainly integration of production technologies to existing DH networks, instead of optimisation of heat supply in building areas linked to DH network. Interconnection of 5 different separate DH systems are studied in Dominkovi? et al. [5] by using a linear optimisation model with an hourly time resolution. In this study, energy production capacities of each DH system were optimised and investments in DH network infrastructure were optimised. Results show that interconnecting geographically distributed DH grids reduces primary energy consumption, emissions and total costs. Effects of supply of excess heat generated by SCs from net zero energy buildings to local DH network were studied in the case of Denmark in Nielsen and Möller [6]. In this study, 3 different DH systems and 3 different technology development scenarios were analysed. The main findings were that excess heat from buildings can decrease utilisation of combustible fuels. In addition, utilisation of seasonal heat storage is essential for the local DH network due to seasonal nature of supplied excess heat. In Verda et al. [7], optimal mix of Ground Source Heat Pumps (GSHP) and DH in small town in Italy was examined from primary energy consumption point of view. According to this study, energy based sustainability of heat supply depends on annual energy consumption, population density and efficiency of heat production.
The studies above concentrate mainly on system based optimisation from the DH network point of view, however, there are several studies concerning optimisation of energy systems consisting of several buildings. Morvaj et al. [8] presents optimal design and operation of distributed energy systems, including optimal heating network layouts, for different scenarios in the area consisting of 11 buildings. In Renaldi et al. [9] integration of heat storage to HP based residential energy system in United Kingdom is examined in terms of optimisation framework. In this study, operational optimisation of HP and storage, combined with heat demand model, is used to manage variable electricity tariffs. In Beck et al. [10] optimal operation, system configuration and optimal sizing for residential energy system with HPs, heat storages and PVs are analysed with MILP model in several scenarios. Furthermore, in Fischer et al. [11] HPs and heat storages in German residential area are optimised in terms of operation and sizing in connection with renewable electricity generated by PVs. Results in this study are compared to established German sizing procedures. However, none of these building specific studies analyse the link between distributed energy production and existing DH networks. This link is though analysed in Dominković and Krajačić [12] in terms of optimal energy storage sizing in urban district cooling system, furthermore, this study also concentrates on optimal sizing of renewable energy production such as PVs. The methodology in Dominković and Krajačić [12] is close to methodology of the research presented in this paper. Kontu et al. [13] pose a question, whether DH can compete with real estate owners' return expectation, taking into account the improved cost-efficiency of residential HPs. This study concludes that HPs are highly profitable for several customer types, but with new dynamic pricing models competiveness of DH can improve significantly. Furthermore, in Wang [14] cost-efficiency of individual HPs versus DH is examined from a levelised cost of energy point of view in the United Kingdom case by using smart meter based data. The results indicate that cost-efficiency of DH depends on the size of the network and in the UK individual gas boilers outperform HPs in terms of levelised cost. Furthermore, in Gustafsson et al. [15] DH and HPs were compared in terms of life cycle cost of heat supply in an area with detached houses by using Monte Carlo simulations. This study concludes that local conditions should be considered when deciding whether DH should be expanded into areas with detached houses.
The authors in [16]-[18] study the impact of applying marginal costs based hourly pricing in context of DH, similar to the common electricity market design. Using marginal costs based pricing was found to ensure cost-efficient dispatch of the heat supply resulting in cost savings. However, based on its case study in Netherlands, Liu et al. [16] found out that the market revenues were not sufficient to cover the investment costs for all heat producers. On the other hand, in Syri et al. [17] a case study in Finland resulted in a conclusion that the open heat market would benefit all parties. In Dominković et al. [18], dynamic pricing of DH was examined from the technology point of view. The marginal costs of DH heat supply are used in the presented research, similarly as in Kensby et al. [19]. There, the use of marginal costs as a price signal for building-specific Exhaust Air Heat Pumps (EAHP) was found to result in costs savings. For the operation of large-scale HPs, marginal costs based pricing had even a more pronounced impact.
The purpose of our paper is not to analyse integration of a building area to DH network but, on the contrary, analyse the effects of increasing distributed production in a residential area connected to DH. This results in increased self-sufficiency in terms of heating and a partial separation from the centralised DH supply. The renewable energy production capacities and hourly operation in terms of heating inside building area are optimised in order to minimise annual total costs, including annualised investment costs, under constraints representing decreasing heat supply from the DH network. This study aims at finding the most suitable energy production mix, consisting of GSHP, EAHP, SCs producing heat energy supported by heat storages and PVs generating electricity, for an increasingly self-sufficient building area. However, the building area can be considered to be integrated to DH network by the ability to sell surplus heat to the DH network. The main contribution of the paper is its effort to combine aspects and methods found in the literature for a realistic case study with measured heat consumption data available. The results are also highly interesting for cities like Helsinki (Finland) where fossil-based centralised DH heat supply is to be replaced with a low-carbon alternatives in the coming decade.
Linear optimisation model is used to find cost-optimal hourly operation of energy system and optimal investments in energy supply units in the case of a single separate building area (described in detail in the next subchapter) by minimising the total annual energy system cost including annualised investment costs. In the model, the heat supply of the building area consists of own production (mainly HPs) and DH purchased from the DH utility. In Appendix I, structure and equations of the optimisation model is described in detail. Optimisation model was implemented by using General Algebraic Modelling System (GAMS) environment. It should be noted, that model used in this paper does not include any financial transactions between the buildings in the area in the case transmission of surplus heat occurring from building to building, that is, the area is considered an energy consuming community optimising the common good. Also, the (other than HP-based) domestic electricity consumption of the buildings is ignored in the model.
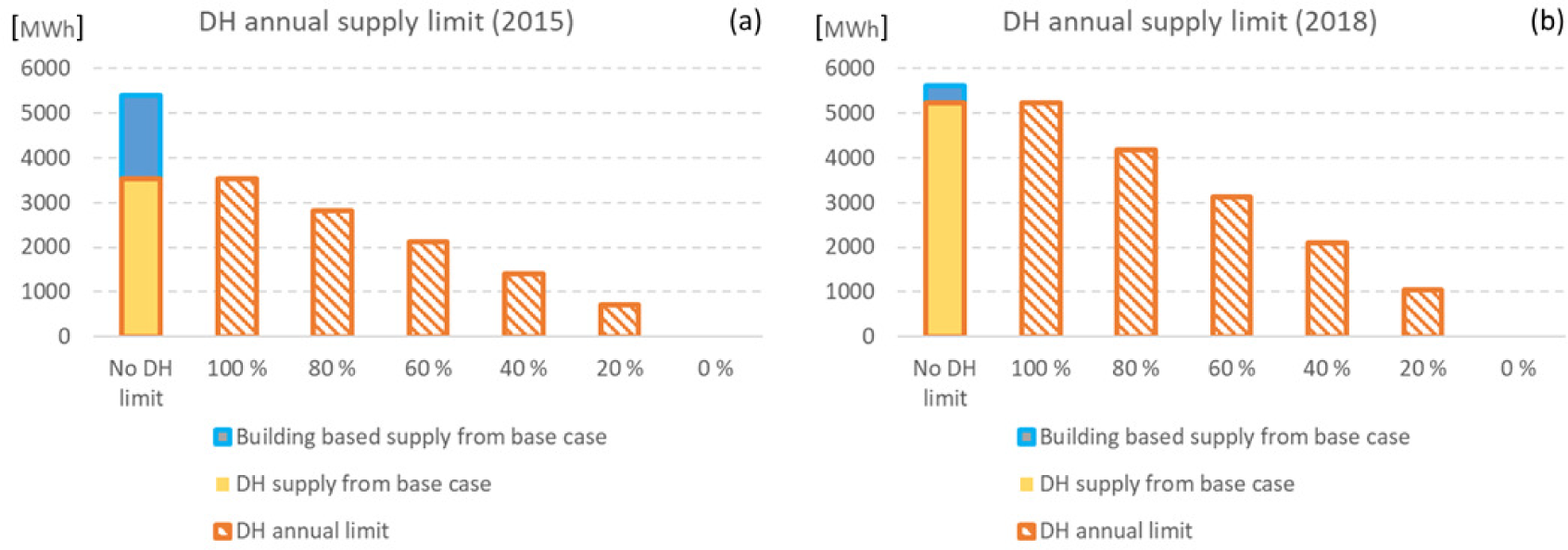
Cases for decreased supply of DH are constructed by first running a base case without any DH limit. Level of DH supply from results of this base case is used as basis for 100% case as illustrated in Figure 1 separately for 2015 and 2018 cases. The annual level of DH supply is then decreased by 20% steps until DH supply is eliminated. In the case of low DH temperature, same supply level limits are used as in the normal DH temperature cases. In addition to cases with decreased DH supply level, a reference case, in which distribution of heat between buildings is eliminated and supply of heat from DH network and centralised ground HP is also removed, is used for system cost comparisons.
The basis for model constraint for annual DH supply in building area in 2015 (a) and 2018 (b)
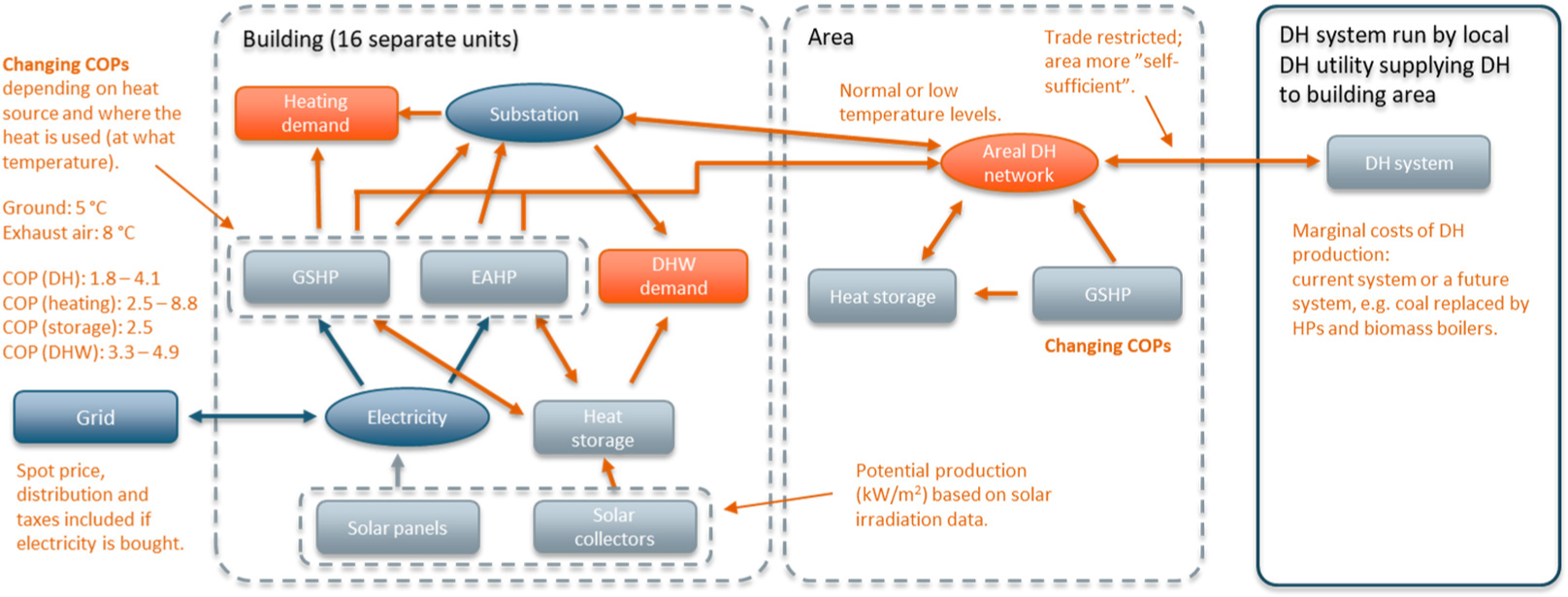
The residential area of Tali in the Finnish city of Helsinki is used as a case system for the analysis. The area is connected to the Helsinki DH network run by Helen, the local utility. Helen currently produces DH mainly by natural gas and coal based Combined Heat and Power (CHP) plants and boilers added with HP production. The Tali area optimises its own heat supply and DH utility (Helen) optimises its own DH production (this DH optimisation by utility is not included in this study), that is, these energy communities are connected merely via DH related trade. Since the building area is connected to the DH network, there is an internal DH network structure inside the area and this interconnecting network is called in this study as areal DH network. In this study, centralised HP stands for a GSHP connected to the areal DH network and operated by the building area.
Measured hourly DH consumption data and basic information on the connected buildings are the main input data used. Table 1 presents the key parameters describing the Tali area. The demand time series are further refined into separate Space Heating (SH) and Domestic Hot Water (DHW) time series. Furthermore, constraints for the optimisation concerning, e.g., maximum capacities for different types of heat and/or electricity production are estimated based on the input data. Parameters such as Coefficient of Performance (COP) for HPs are also pre-calculated, although they are more general in nature and not related only to the case system. Table 2 below lists the input data used for the modelling and provides details on principles, assumptions and methods.
While the used input assumptions on costs concerning, e.g., electricity or DH prices are reasonably robust, the investment costs are naturally estimations and remain always a point of discussion. It should be noted, that different sources can state different costs and the real costs are always affected by the location and, e.g., type of building where they are installed. However, the magnitude and the order of the costs assumed should be reasonable. Figure 3 below presents the principled structure of the model with optional components for the optimisation to choose from included.
Key parameters describing the case system of Tali in Helsinki, Finland
| Key parameter | Value |
|---|---|
| Number of consumer buildings | 16 |
| Total floor area [m2] | 38,000 |
| Local distribution network length [m] | 1,400 |
| Total DH consumption [GWh] | 5.6 (average) |
| Share of DHW consumption [%] | 45† (average) |
| Heat demand density [MWh/m] | 4.0 |
Share of DHW consumption is high due to the bathroom comfort heating systems
Definition of input used by the optimisation model
| Input data | Method and main assumptions |
|---|---|
| Heat demand time series for SH and DHW | As no SH demand is present in summertime, this period is copied throughout the year to generate separate time series for DHW and by subtracting this from the total demand, for SH. Individual hours with missing or excess demand during spring/autumn are added to the SH demand or omitted if the resulting SH demand would drop under 0 kWh/h. |
| GSHP maximum capacity | Maximum capacity is defined as the total maximum demand during a year. |
| EAHP maximum capacity | The capacity is calculated using the data on building volumes and by assuming 0.5 air changes in an hour and a 15 °C temperature difference for the airflow through the heat recovery system. |
| EAHP maximum production | Seasonal variation of humidity of the air is taken into account (measurement data from Helsinki, the impact varies between 71-100%), and the maximum production for EAHPs is given as time series. |
| PV panel and SC maximum area | The available roof area available for PV panels or SCs is calculated using the total floor area, estimated number of floors and an assumption that 60% of the roof area can be effectively used for the purpose. |
| Heat storage maximum capacity | Maximum storage size defined as the number of hours times the capacity of a specific heat supply system. The number of hours are 2.5 h and 24 h for building level storages and an area level storage, respectively. The capacity is the defined maximum capacity for a GSHP for both buildings and the area. |
| HP COPs | COP time series for the HPs (EAHP, GSHP) are calculated for each type of heat use (SH, DHW, storage, DH network). The COPs are based on assumed temperatures of the heat source and the point of demand, e.g., borehole for GSHP (3-8 °C, heat source) and radiator inlet and outlet temperatures (outdoor temperature based control, varying, e.g., 70-40 °C for inlet) common in Finland. Carnot efficiency of 35% is assumed. |
| Investment costs | Investment costs for each technology are estimated according to Pardo Garcia et al. [20]. |
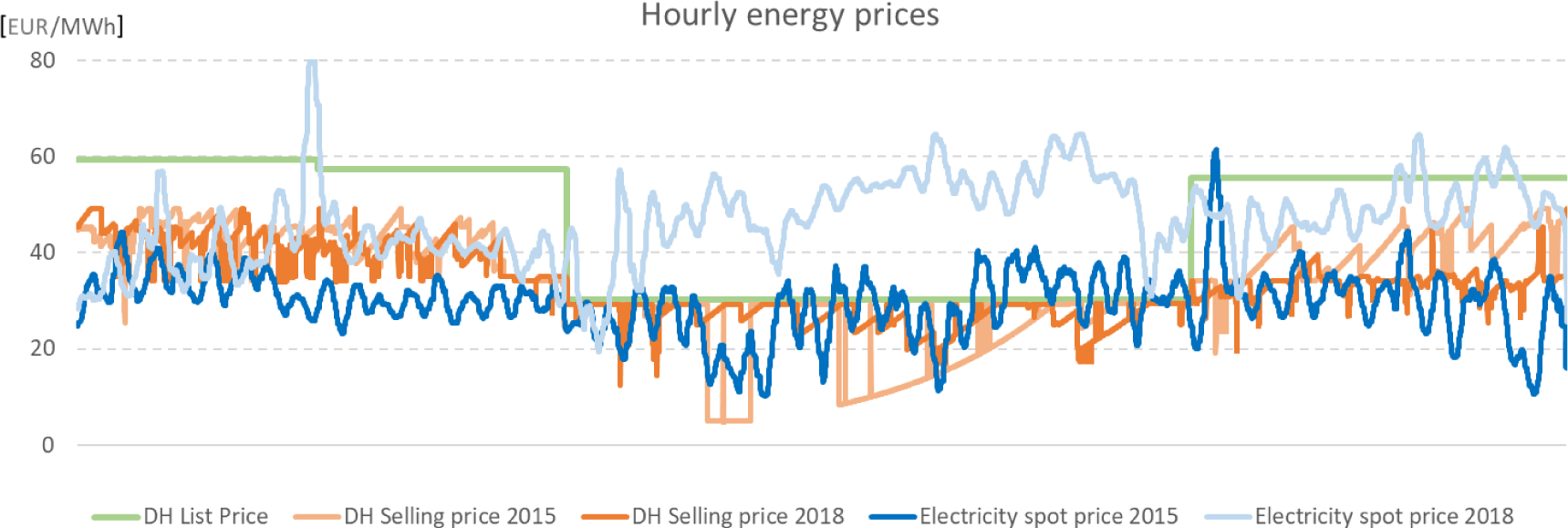
| Other costs | Other costs include electricity prices (market price, grid costs, taxes [21]-[23]), DH tariffs [24] for heat purchased and modelled hourly DH marginal prices, using optimisation model from Lindroos et al. [25] and current DH production profile from [26], for heat sold to network (see Figure 2 for hourly prices). |
Hourly energy prices used in the model [note 1 – electricity prices illustrated here are 3 day moving average values, note 2 – same DH list price is used for 2015 and 2018 cases (grid fee + taxes for electricity is 55 EUR/MWh)]
The basic structure of Tali building area energy system
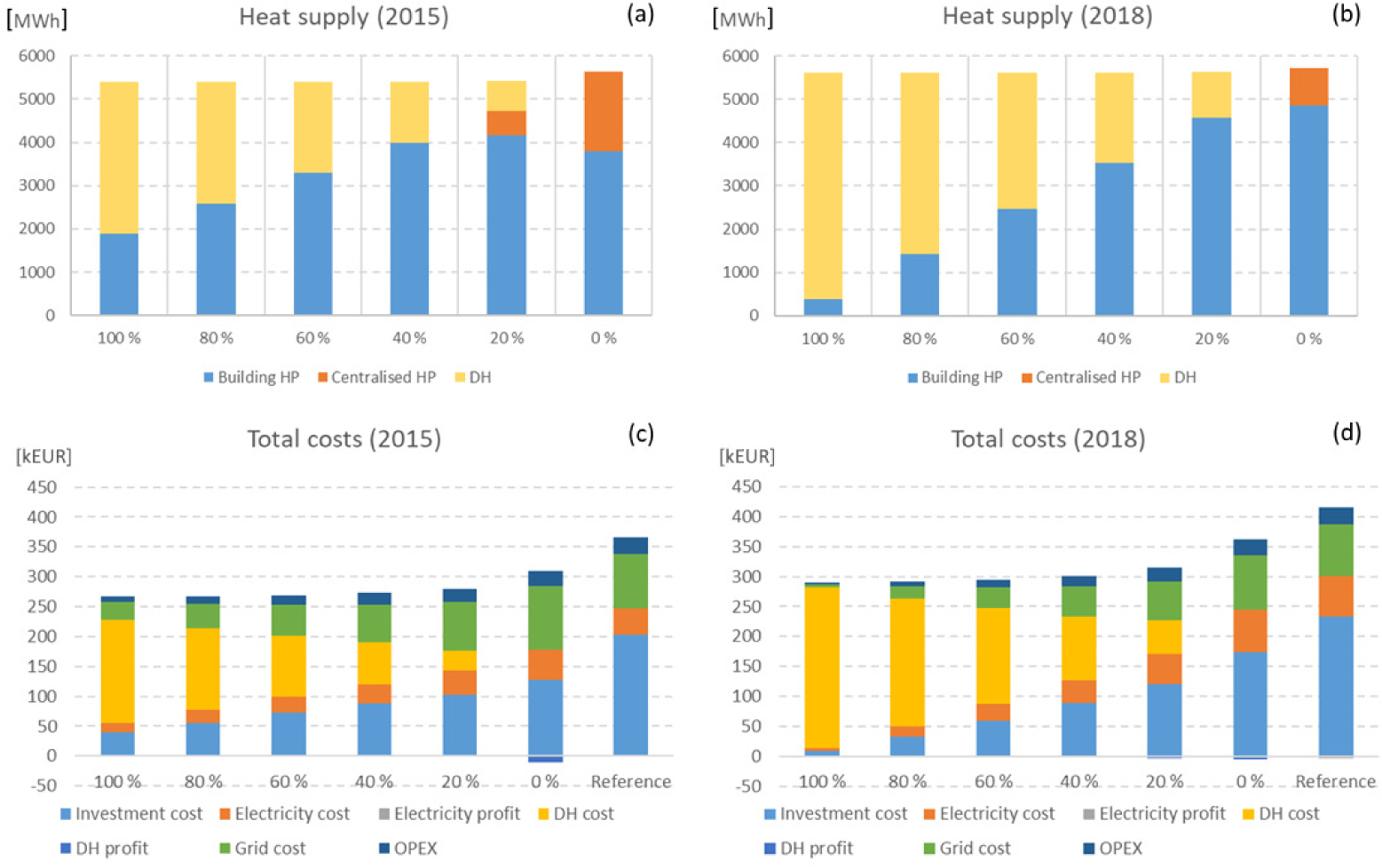
Results presented in this chapter are based on hourly one-year optimisation of the energy system in the building area with constraints concerning DH supply as stated in Figure 1. These results are examined on annual level in terms of heat supply, costs and production capacities. The costs of energy system presented here include annual operating costs, such as electricity cost, DH cost and Operational and Maintenance cost (OPEX), and, in addition, investment costs of all the production or storage technologies added into the energy system. It must be noted that investment costs of each technology are annualised by using discount rate of 7% and investment horizon of 20 years. Profits generated by selling surplus electricity or DH are presented in these results as negative costs. These annual results are presented for cases involving years 2015 and 2018 combined with normal heat supply temperature and low temperature cases.
The heat supply inside the energy system of the building area in the normal heat temperature case is depicted in Figure 4a (year 2015) and Figure 4b (year 2018). In these graphs heat supply is divided into three sources:
Building based HP production;
Areal centralised HP production;
Network based DH (provided by the DH utility).
It must be noted that heat supply varies from the total heat demand of the building area, if surplus heat is sold to DH network. Evidently, building based ground HP production increases as share of DH in system heat supply decreases, with share of building based ground HPs reaching 85% in the 2018 case (77% in year 2015). However, investments in EAHPs or SCs do not appear in any case, due to high cost characteristics of these technologies.
As DH share of heat supply decreases, at 20% and 0% shares, production of centralised ground HP increases in cooperation with centralised heat storage with 33% share in year 2015. Evidently, the centralised ground HP fills the missing heat supply more efficiently than building based HPs. The capacity of centralised ground HP in the 2015 case at 0% DH level is 440 kW (372 kW in the 2018 case) and utilisation factor is 48% (26% in the 2018 case). For comparison, in the same 2015 case, utilisation factors of building specific ground HPs are at 75-78% (64-68% in the 2018 case). In terms of centralised heat storage, in the case of 2018 heat storage has maximum capacity (38,808 kWh) with merely 19 cycles, whereas in the case of 2015, corresponding capacity is 3,366 kWh (9% of maximum capacity) with 73 cycles.
Figure 4c and Figure 4d illustrate total cost of the energy system at different levels of DH supply share. Evidently, total costs of energy system increase, mainly due to investment costs of ground HPs and grid costs of consumed electricity. In the 2015 case total costs are 12% higher at 0% DH supply level when compared to 100% level, whereas in the 2018 case corresponding increase is 24%. However, total cost in reference case, in which DH network is entirely disabled inside the building area, is in all cases higher, that is, 22-37% (compared to 100% and 0% DH share) in 2015 and 15-43% in 2018. Volume of sold surplus heat from building area into DH network is marginal in all cases. Furthermore, in the 2018 case, small volume of surplus electricity generated by PVs is sold to the market. Calculated from the results, the levelised cost of energy for building area is 55 EUR/MWh in 2015 and 64 EUR/MWh in 2018.
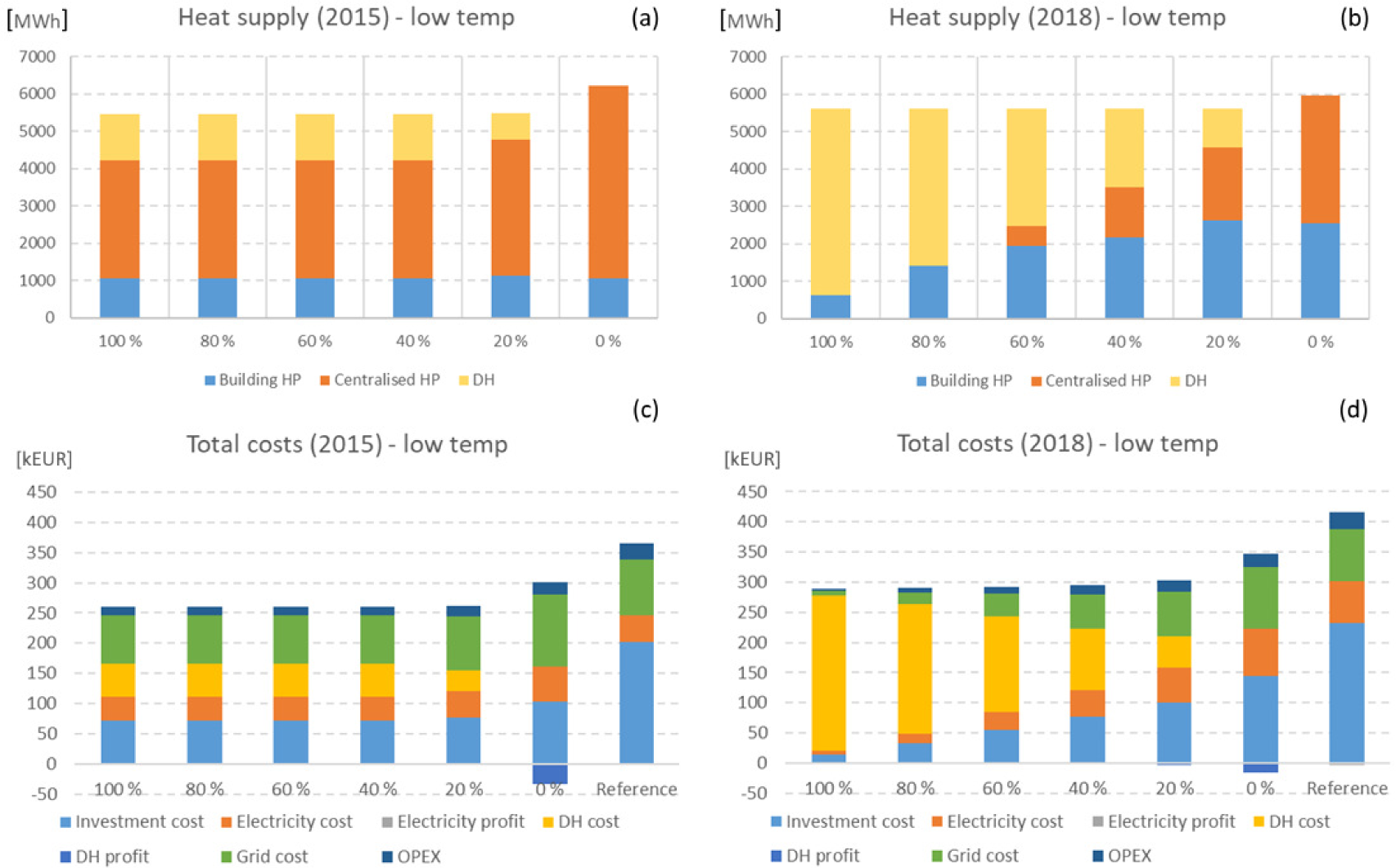
Figure 5a and Figure 5b depict similarly the heat supply of the energy system from the lower heat supply temperature case. In the case of low supply temperature, building specific production investments are at lower level and centralised ground HP dominates heat supply in energy system, especially in the 2015 case, regardless of constraint concerning availability of DH. The high utilisation of centralised HP is based on its higher COP values due to lower supply temperature level. Surplus heat from building area is sold to DH network when DH supply is limited to 0%, 763 MWh in the year 2015 case and 359 MWh in year 2018. Figure 5c and Figure 5d illustrate results in terms of system cost and, evidently, total cost in reference case is in all cases higher, that is, 36-41% (compared to 100% and 0% DH share) in 2015 and 24-43% in 2018. In the year 2015 case profit from sold surplus heat reaches level of 33 kEUR (14 kEUR in 2018). In the low temperature case the levelised cost of energy is 50 EUR/MWh in 2015 and 59 EUR/MWh in 2018.
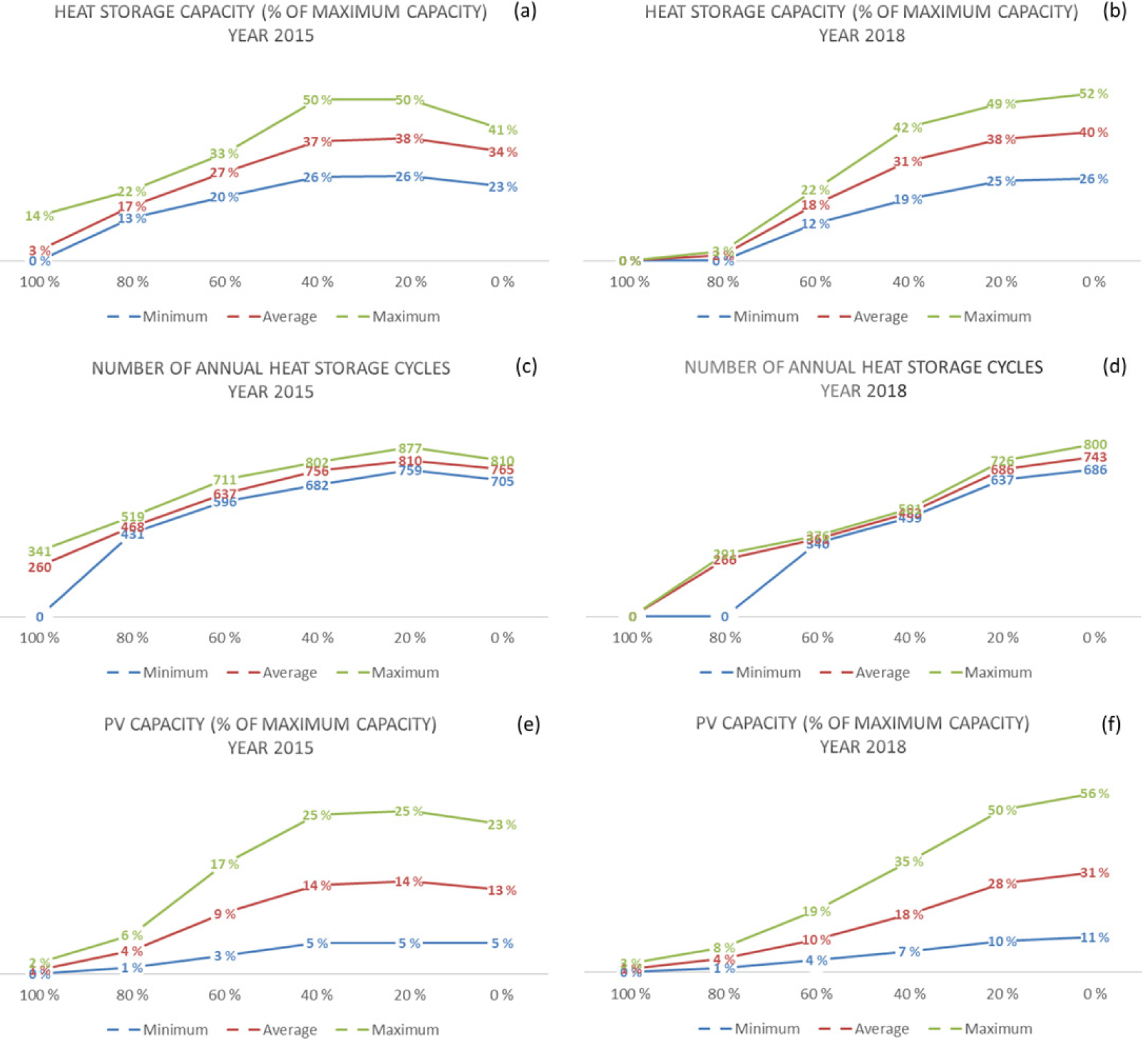
Figure 6a and Figure 6b depict development of heat storage capacity at different levels of DH supply share. These graphs present percentage of installed storage capacity from maximum capacity level defined for each building. As DH supply is limited, heat storage capacity increases in all buildings. In addition, annual number of storage cycles increases, as Figure 6c and Figure 6d state. In the 2015 case storage capacity growth stops at 40% level due to utilisation of centralised ground HP. According to Figure 6e and Figure 6f, PV capacity increases as buildings produce own electricity in order to save costs, especially grid costs. In the year 2018 case, higher electricity prices cause higher investments in PV. In the 2015 case PV capacity growth stops at 40% level, since growth of building specific HP capacity stops at similar level.
Heat supply (a-b) and total costs (c-d) of energy system in building area as a function of maximum share of DH supply in the case of normal DH temperature
Heat supply (a-b) and total costs (c-d) of energy system in building area as a function of maximum share of DH supply in the case of low DH temperature
Development of heat storage capacity (a-b), number of annual storage cycles (c-d) and PV capacity (e-f) in buildings 1-16
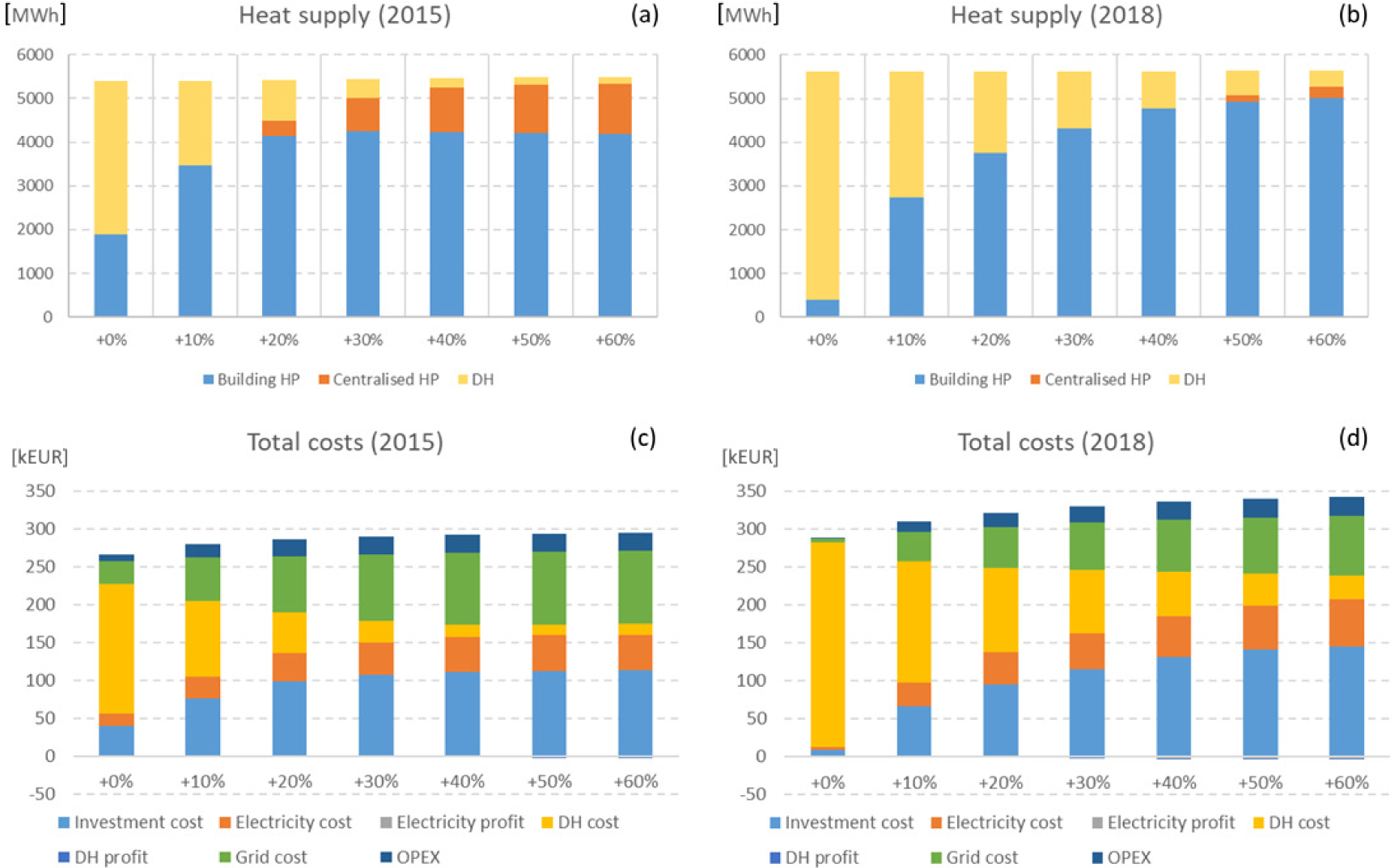
First sensitivity analysis, depicted in Figure 7, concerns price of purchased DH, since, from cost related optimisation point of view, increasing price of DH should decrease level of DH supply and, therefore, increase investments in own production. The base case in this sensitivity analysis has no constraints for DH supply, that is, it is equivalent to 100% case in Figure 1. When DH supply price is increased, building based ground heat production and centralised ground HP production increases in case 2015. However, in the 2018 case, role of centralised ground HP is marginal. In addition, there are no investments in EAHPs or SCs in these cases. Evidently, in year 2015 price effect stops at +30%, whereas price effect stops at +50% level. Furthermore, there is still marginal use of DH despite the price increase of 60%, since during some periods it is more cost-efficient to purchase DH instead of investing in extra HP capacity. Altogether, the total system cost increases but growth is weakened by investments in own production.
Heat supply (a-b) and total costs (c-d) of energy system in building area as a function of increase of DH supply price in the case of normal DH temperature
Another qualitative sensitivity analysis concerns availability of centralised ground HP and centralised heat storage. In this analysis, base cases are normal and low temperature cases based on year 2015 and DH supply levels of 40, 20 and 0%. In the sensitivity cases centralised heat storage is disabled from the energy system (No DST'), centralised ground HP is disabled (No DHP') and both technologies are disabled (No DHP + DST'). Figure 8 depicts difference between these cases and base cases in terms of total annual cost. Evidently, in 2015, in the normal temperature case, removal of heat storage has greater effect than removal of centralised ground HP, whereas, in the case of low DH temperature, effect of HP removal is greater. With normal temperature, No DHP' case produces only 2% higher total cost compared to base case, whereas No DST' case produces 6% higher total cost. On the other hand, with low temperature, No DHP' case produces 8% higher total cost (5% in No DST' case). According to Figure 8, the main reason for larger costs is increased investment costs, whereas there are increased profits from sold surplus heat due to the absence of the centralised heat storage. When considering the effect of the investment cost of the centralised HP on the results, it should be mentioned that the role of centralised ground HP diminishes greatly, in the case of normal temperature, when its investment cost approaches the investment cost of building specific ground HP.
Finally, one distinct characteristic in the base results is the lack of capacity in terms of EAHPs and SCs in the buildings. Therefore, a simple sensitivity analysis in terms of investment costs of these technologies was performed. In this analysis, the 2018 case at 0% DH supply level was used since building specific heating (ground HPs only) has highest share from heat supply amongst all cases. In separate cases, the investment cost of SCs and EAHPs is decreased until buildings start investing in these technologies. According to the sensitivity analysis, the investment cost of SCs must decrease 65% for any capacity to appear, and the level of capacity is at 0-9% of the building specific maximum capacity. In the case of EAHPs, investment cost has to decrease 30% in order to have capacity in buildings (44-100% of maximum capacity).
Difference in in total cost between regular case and cases with centralised heat storage removed (No DST'), central ground HP removed (No DHP') and both removed (No DHP + DST') in year 2015 in the case of normal DH temperature (a) and low DH temperature (b)
Firstly, the model limitations must be discussed here. First, the proper modelling of the electricity consumption of the HP due to the heat type (heating, hot water, DH and heat storage) produced requires several binary variables for each hour and each building. This modelling option requires MILP and produces over million binary variables in the model. Solving time for such an optimisation problem can rise to several hours and therefore such an approach is not usable in this study due to the large number of cases run. Secondly, linear model defined in Appendix I enables simultaneous transfer of DH out of the building (to another building) and in to the building (from DH network for DHW). This rarely occurring issue could also be blocked by using binary variables in the heat balance equations. Overall, using linear programming can be justified by reasonable accuracy of the model and short solving time.
Secondly, in practice, the situations where the DH supply is heavily constrained, the system might also have trouble in maintaining high enough temperature level as the buildings supply much of their own heat demand and as a result, the flow in the network is greatly reduced. The situation is similar than in low heat demand areas in general. In fact, as the local heat supply grows the effective heat demand density in terms of centralised DH supply drops close or below one MWh/m (a common threshold value for defining low heat demand areas). Preliminary network simulations indicate that at the least the low temperature distribution cases with high share of distributed heat production can encounter the problem of maintaining high enough temperature level without any special arrangements to maintain the temperature level such as e.g. by-pass valves.
Finally, the issue concerning consumers turning into producers in the DH network should be addressed briefly here. From the DH company point of view, it should be noted that, since selling price is based on the marginal cost of the produced DH, significant amount DH sold by several districts affects the marginal cost of DH and therefore profitability of sold DH. In addition, transformation of consumers into producers in significant numbers affects customer base and volume of sold DH. This complex system dynamic issue should be considered by the DH company when opening the DH market for small producers.
The study carried out represents an interesting case for increasing amount of renewables in a DH system by adding distributed, mainly HP based heat production capacity into the system. Availability of heat sources from a viewpoint of a large-scale DH system is a challenge as urban heat sources tend to consist of small, scattered sources. Exceptions such as data centres or wastewater treatment plants do exist, but it is unreasonable to generalise that they would be available for every large-scale DH system - and even then, it is likely that more is needed. From a business model perspective, the study in hand corresponds to an energy community as heat trade between consumer buildings is allowed without the involvement of the DH production company. Only the surplus heat produced within the whole area is sold to the DH system. One option would be a more controlled approach, where the heat produced in a specific building would be sold directly to the DH company - or the DH company itself would be investing and controlling the building specific units, sharing the benefits of using the heat sources between itself and the consumer.
The results presented in this paper raise interesting questions on self-sufficiency from DH. Why is centralised ground HP combined with centralised heat storage included in the energy system? Is self-sufficiency in terms of independence from district heat network beneficial to the building area? Is there potential for buildings to sell surplus heat to district heat network? According to the modelling results, at the lower share levels of DH supply the centralised ground HP supplements set of building based HPs by covering varying heat load, even though utilisation rates are at lower level than in the case of building specific HPs. Furthermore, centralised heat storage plays against varying electricity by scheduling electricity consumption of centralised HP in a more cost-efficient manner. In the low temperature case centralised GSHP benefits from the higher COP values and provides the majority of the heat supply in the building area. However, the significant role of centralised HP is partly based on its lower investment cost.
One point clearly seen from the results is to show how the development towards a net zero residential area operates in general and from the DH company point of view. In economic sense, the constraints on the use of utility-based DH increase the total costs of running the system. On the other hand, the cost increases with moderate constraints are small and could be argued to be worth the new, added renewable heat supply. However, if this development hurts the economic feasibility of having a DH system at first place, it is interesting to take note that the costs of a system without a network at all are significantly higher.
Under increasing self-sufficiency from DH, the building community invests increasingly in ground HPs to provide heating, heat storages to manage the heat load and PVs in order to provide electricity to HPs and avoid relatively high grid fees due to own electricity generation. However, this increasing trend is dampened in the community by investment in centralised ground HP and heat storage. Evidently, in the case of normal DH supply temperature, the most cost-efficient manner for a building to disintegrate from the DH network is to invest in a package consisting of ground HP, heat storage and PVs. This is also evident in the case of disintegration from the DH network due to increase in DH price. Overall, disintegration from the DH network inflicts 12-24% higher annual total costs when compared to case with unconstrained link to DH network.
The modelling results indicate that with energy production options available investments in EAHPs and SCs do not occur. It is obvious that noteworthy properties of SCs, that is hourly availability and investment cost, are not usable from the building area perspective. In the case of EAHP, the ground HP technology is superior unless investment cost of EAHP is decreased by 30%.
Finally, according to the modelling results, sales of surplus heat to local DH network are in all cases marginal, and this transaction occurs merely when DH supply from network is set to be at 0% level. Main reasons for this lack of DH commerce are the ability of the energy community to invest optimally in own production and storage capacity and relatively low selling price based on marginal cost of produced DH. Evidently, extra investments in production are not worthy due to electricity prices and investment costs when reflected to DH selling price.
The authors would like to acknowledge the EU Horizon 2020 project mySMARTLife [731297] for financial support for this work.
- , Heat Pump Placement, Connection and Operational Modes in European District Heating, Energy Build., 2018
- , Introducing Modern Heat Pumps to Existing District Heating Systems Global Lessons from Viable Decarbonizing of District Heating in Finland, Energy, 2019
- , Heat Roadmap Europe: Large-Scale Electric Heat Pumps in District Heating Systems, Energies, 2017
- , Integration of Storage and Renewable Energy into District Heating Systems: A Review of Modelling and Optimization, Sol. Energy, 2016
- , On the Way Towards Smart Energy Supply in Cities: The Impact of Interconnecting Geographically Distributed District Heating Grids on the Energy System, Energy, 2017
- , Excess Heat Production of Future Net Zero Energy Buildings Within District Heating Areas in Denmark, Energy, 2012
- , Reduction of Primary Energy Needs in Urban Areas Trough Optimal Planning of District Heating and Heat Pump Installations, Energy, 2012
- , Optimising Urban Energy Systems: Simultaneous System Sizing, Operation and District Heating Network Layout, Energy, 2016
- , An Optimisation Framework for Thermal Energy Storage Integration in a Residential Heat Pump Heating System, Appl. Energy, 2017
- , Optimal Operation, Configuration and Sizing of Generation and Storage Technologies for Residential Heat Pump Systems in the Spotlight of Self-Consumption of Photovoltaic Electricity, Appl. Energy, 2017
- , Impact of PV and Variable Prices on Optimal System Sizing for Heat Pumps and Thermal Storage, Energy Build, 2016
- , District Cooling Versus Individual Cooling in Urban Energy Systems: The Impact of District Energy Share in Cities on the Optimal Storage Sizing, Energies, 2019
- , Individual Ground Source Heat Pumps: Can District Heating Compete With Real Estate Owners Return Expectations?, Sustain. Cities Soc., 2020
- , Heat Pumps With District Heating for the UKs Domestic Heating: Individual Versus District Level, Energy Proc., 2018
- , Life Cycle Cost of Heat Supply to Areas with Detached HousesA Comparison of District Heating and Heat Pumps From an Energy System Perspective, Energies, 2018
- , The Marginal-Cost Pricing for a Competitive Wholesale District Heating Market: A Case Study in the Netherlands, Energy, 2019
- , Open District Heating for Espoo City With Marginal Cost Based Pricing, Proceedings of the 12th International Conference on the European Energy Market (EEM), 2015
- , Influence of Different Technologies on Dynamic Pricing in District Heating Systems: Comparative Case Studies, Energy, 2018
- , Heat Source Shifting in Buildings Supplied by District Heating and Exhaust Air Heat Pump, Energy Proc., 2017
- , , Best Available Technologies for the Heat and Cooling Market in the European Union, JRC Scientific and Policy Report, 2012
- , , Historical Market Data 2019
- , , Electricity Distribution Prices for Helen 2019
- , , Energy Taxation in Finland 2019
- , , District Heating Prices for Helen 2019
- , Robust Decision Making Analysis of BECCS (Bio-CLC) in a District Heating and Cooling Grid, Sustain. En. Tech. Asses., 2019
- , , District Heating Statistics 2016, Mater Bank 2017, 2017




