The existing model used in this work, urbs, is an open-source linear optimization tool programmed in the language Python developed by the Chair of Renewable and Sustainable Energy Systems of the Technical University Munich (TUM). This model identifies the optimum economic configuration to meet the predetermined resource demand at the lowest feasible cost. The minimal total cost results from the techno-economic modelling of all conversion, transmission, and storage processes. A detailed description of the complex mathematical processes behind this optimization tool can be found in [10].

Initially, urbs was designed to optimize energy systems. Previous studies in urbs focused on grid-connected and microgrid renewable energy systems, for example, the works of [12] and [11]. However, urbs can be adapted to design and optimize least-cost EWF systems, thus interconnecting different sectors in circular processes. The works of [13] and [14] present the previous versions of the urbs optimization model for EWF systems. This work adds up to the previous urbs version, focussing on improving the hydrogeological sector of the model.

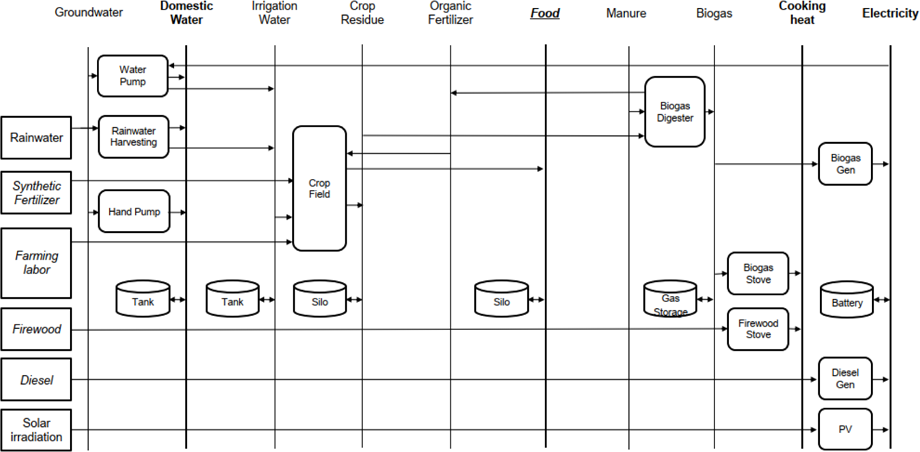
Figure 1 shows the flow diagram of the model. Here, it can be seen which combination of commodities can be transformed into other commodities through defined processes. Each process comprises a unit ratio for input and output commodities (e.g., m³ of groundwater for a kg of tomatoes) and a cost per unit processed.

The approaches to developing the model are based on two conventional hydrogeological models: the Soil and Water Assessment Tool (SWAT) and the modular finite-difference flow model (MODFLOW). Hydrological and hydraulic models combined can simulate the water flow in two or three dimensions [15]. SWAT is a watershed scale model to predict the impact of land management practices on water, sediment, and agricultural chemical yields. The model is physically based and requires input data from weather, soil properties, topography, vegetation, and land management in the watershed. Then, it models the physical processes of water and sediment movement, crop growth, nutrient cycling, etc. [16]. MODFLOW is an international standard for simulating and predicting groundwater conditions and interactions with surface water. MODFLOW simulates groundwater systems, solute transport, variable-density flow, aquifer-system compaction, and land subsidence Click or tap here to enter text..

It is necessary to define the sustainable limits of the natural environment to guarantee that the resulting system can be operated long-term. In this model version, the sustainability frame indicates that the system can use only the rainwater infiltrating the community area.

Figure 1.

Flow diagram of the urbs model for EWF systems [14]

As the model can be implemented in remote regions, which often do not have access to reliable data, the model results may be affected by uncertainty. Therefore, this work assesses the impact of data uncertainty on the most relevant hydrogeological input parameters.

The developed model is applied to the case study of the Jesuit mission St. Rupert Mayer (SRM) in Zimbabwe. SRM is located 200 km west of the capital Harare, in a rural area with a low population density. The main income sources are agriculture and farming on a small scale, producing maize and vegetables. The mission offers the following services: hospital, preschool, primary school, high school, and a church. The community's water supply now depends on rainfall and electric pumps. Then again, the energy supply for the pumps depends on the centralized supply from the Zimbabwean Electricity Security Authority and on diesel (which often is complicated to obtain). Consequently, in the dry season, there is no water supply if there is no energy supply.

These calculations prepare the input data for the hydrogeological processes in an Excel datasheet based on the equations used in the programs SWAT and MODFLOW. The outputs of this tool are net rainfall, aquifer parameters, and water demand.

Net rainfall

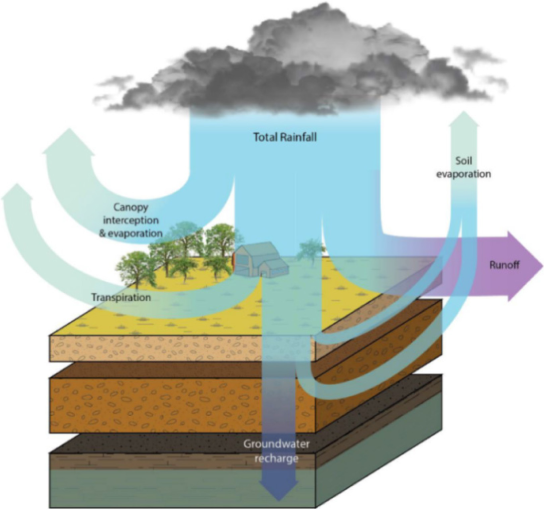
Calculates the losses from the total rainfall due to the following factors in a daily resolution: canopy interception and evaporation, runoff, transpiration, soil retention, and soil evaporation. The "net rainfall" is the amount of rainwater that can be used in the model. The involved hydrogeological processes are presented in Figure 2.

Figure 2.

Natural processes involved in the calculation of the net rainfall

The most important input parameters include reliable rainfall data. A suitable option is the remote sensing data from the Tropical Rainfall Measuring Mission (TRMM) [19], [20].

Similar to the calculation approaches of the SWAT program, the community's area is subdivided into "Hydrological Response Units (HRUs)". These subareas are classified depending on land use, topography (slope), soil type, and vegetation [15]. This assessment and the calculation of the HRUs can be made using Geographic Information System (GIS) tools and digital elevation models. For this model setup (adapted to the case study), the HRUs are grouped in three different sectors, which have different processes for the falling rainfall:

Crop fields − the rainfall can supply the crops’ water demand directly and recharge the aquifer. The net rainfall is the sum of the groundwater recharge plus the retention in the top soil and unsaturated zone (UZ), minus the soil evaporation.

Area outside the crop fields minus the area of buildings − this sector can be subdivided into different land uses (HRUs), such as fallow land (B.1) and forest (B.2). The rainwater falling in this sector can only be utilized if it reaches the aquifer.

Building roofs − the rainwater falling in this sector can be harvested to supply the domestic water demand.

The following hydrogeological processes are calculated daily in the pre-urbs tool:

• Evapotranspiration − depending on the potential evapotranspiration and water available.

• Interception − the rainfall volume intercepted by the vegetation, which can evaporate depending on the Leaf Area Index (LAI) and climatological aspects [21], [22]. The tool calculates the daily amount of rainfall stored and evaporated and the amount exceeding the retention capacity.

• Runoff − this quantity depends on the slope, soil type, vegetation, and dryness or saturation of the ground, as well as on the rainfall intensity [23]. The calculation employs the Soil Conservation Service runoff equation [24], considering the previous rain events.

• Transpiration − the amount of water consumed by the plants depending on their morphology and growth phase and available water. For the B sector areas (forest and fallow land), this process is a "water loss".

• Soil evaporation − if the potential daily evaporation has not been met after canopy evaporation and transpiration, a certain volume will evaporate from the soil's water retention. Depending on the climatic and geological circumstances, the water can be extracted from the top soil or deeper layers. This amount depends on the degree of shading and the extent of biomass above the ground (vegetation) [22].

Soil and Aquifer data

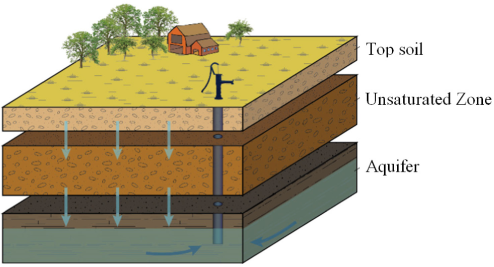
The urbs model conceives three ground layers: the Top Soil layer (TS), the Unsaturated Zone (UZ), and the aquifer (Aq), as can be seen in Figure 3.

Figure 3.

Ground storage units in urbs

The soil evaporation and the water amount exceeding the retention capacity are calculated daily to indicate the volume percolating to the lower ground layer. The groundwater flow is described by Darcy's Law [22], whereas the rate at which the infiltrated water reaches the water table depends on the thickness of the UZ [25]. The relation between rainfall and percolation is directly related to the annual rainfall pattern (intensities) [26], [27]. As the aquifer’s water-storage capacities may vary greatly over short distances [28], extensive measurements should be done onsite to define the structure of the aquifer. General geological data, for example, the Quantitative Maps of Groundwater Resources [29], constitute an option for rough estimations of the aquifer structure.

The urbs model operates with a complex Python optimization code, which gathers input data from a structured Excel document. It includes all hydrogeological processes directly affecting the water availability per time step and the system's costs. The model flow diagram can be seen in Figure 4. The model input data are classified in:

• Demand − defined in m³/h of each water type;

• Commodities − resources including their prices per unit [€/m³];

• Fluctuation supply − availability of natural resources at each time step;

• Processes − specification of costs and efficiencies involved (e.g., transport capacities [m³/h], annual fixed costs [€/y per m³/h], etc.);

• Process-Commodities − the ratio between input and output commodities for every process;

• Storage − storage units for a specific commodity, including a percentage loss per hour (represents tank leakages or evapotranspiration).

Figure 4.

Flow diagram of the water component of the urbs model

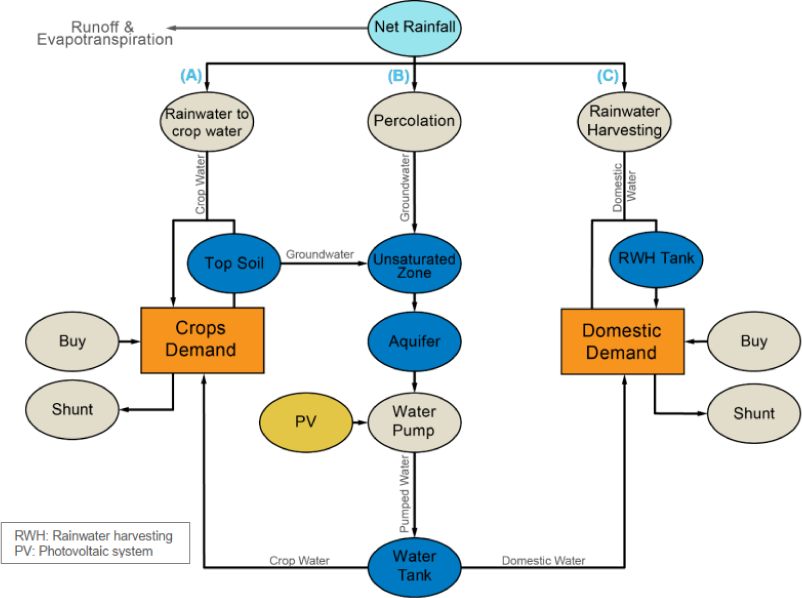
As can be seen in Figure 4, the domestic water demand is supplied from the pumped groundwater and harvested rainwater, whereas the crop water demand is supplied by:

• Rainwater − calculated by multiplying the net rainfall by the crops area and used in three ways: 1) to supply the demand directly; 2) if its volume is greater than the demand, the rest is stored in the top soil for later use; 3) percolation to deeper layer if the top soil is saturated.

• Irrigation − if the usable rainwater does not cover the demand, the missing volume is supplied through irrigation. The total Irrigation Delivery Requirement (IDR) includes the plant watering requirement and the water losses for distribution.

The system will buy water if the local water resources are insufficient to cover the demand. This also indicates that the system is not self-sustainable and should be improved (e.g., by changing the crop types for ones consuming less water).

The net rainfall is introduced into the model as an intermittent supply input. It is modelled as a change in capacity (a capacity of 100 % represents a rainfall of 10 mm/h) multiplied by the area of each HRU.

The ground layers are represented as storage units with specific urbs properties: storage capacity, input-output capacity (representing infiltration), and hourly discharge (representing soil evaporation). For simplification, it is assumed that the ground is homogenous in all directions and completely interconnected. The infiltration rate is modelled by adopting the methods of the program MODFLOW, which calculates the groundwater flow in three-dimensional ground units [18]:

• Top soil storage (TS) − the storage capacity is calculated as the crops area multiplied by the root depth and water percentage available for the plants (soil porosity minus the wilting point). The commodity stored is Crop Water and is affected by soil evaporation.

• Unsaturated Zone, modelled analogously to the top soil. It buffers the water path from the top soil to the aquifer, which is modelled as a transfer from the TS unit into the UZ at a given (percolation) rate. The stored water cannot be used.

• Aquifer − for simplification, represented as a shallow unconstrained aquifer. The total volume is the community area multiplied by the aquifer depth and the usable storage capacity.

The model's infrastructure system is composed of a solar pump, photovoltaic panels, and a storage tank, which are dimensioned to optimize all costs. To generate electricity, the process "PV" converts the fluctuating resource solar irradiation into electricity, where the efficiency is determined by the solar capacity factor per time step. In the solar-pump process, electricity and groundwater are the inputs with specific ratios, and "pumped water" is the output. This commodity is stored in tanks and can be transformed into "crop water" or "domestic water" to supply the respective demands. The pump size is limited by the aquifer's extraction capacities. The pump rate should be obtained by performing pump tests onsite. The hydraulic sizing of the submersible pump represents the electrical power needed to pump one cubic meter of groundwater to the storage tank, considering the dynamic groundwater level and the system efficiency.

Because of the uncertainty of the available data, it is necessary to identify which input parameters have a greater impact on the model results. Some parameters may need exact input data to obtain reliable results.

The base scenario consists of one solar pump to cover the water demand of 15 ha of Maize with three harvests per year and a community of 600 people. For this analysis, the following parameters are to be tested:

• Maximum pumping rate (max. Q) − the limit of the pumping rate must be based on aquifer characteristics. The values used are 0.1, 0.5, 1.0, 1.5 and 2.5 l/s

• Aquifer hydraulic conductivity (K) − affecting the infiltration rate and storage capacity. The values used are K = 8E-07 m/s for the base scenario, 3E-04 m/s for the best-case scenario, and 8E-09 m/s for the worst-case scenario (fractured metamorphic rock) [35].

• Aquifer storage capacity − in the base scenario, the aquifer area is the area of the whole community, assumed to be completely interconnected (every water drop percolating anywhere could be extracted by the pump). For the worst-case scenario, the aquifers area is 0.75 % of the community area and has a hydraulic conductivity of K = 8E-09 m/s.

• Land use − two scenarios are analysed: 1) deforestation scenario, 73.7 % of the forest area is converted into fallow land; 2) afforestation scenario, the forest area increases 66.5 %

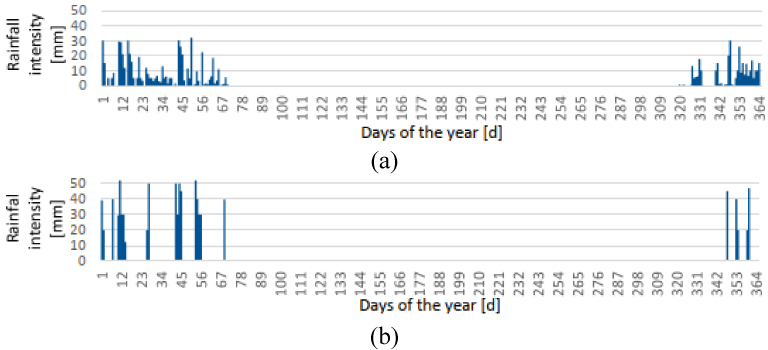
• Rainfall pattern − different scenarios are analysed, representing changes due to climate change and local environmental changes. Two artificial rainfall patterns with the same total rainfall amount (864 mm/y) are considered. In the first scenario, the daily rainfall intensities are reduced, and the total rain volume is distributed over more days in the wet season (mid-November to mid-March). In the second scenario, the daily rainfall intensity is increased, and the number of rainy days is reduced, concentrating the water volumes on fewer days. These rainfall patterns can be seen in Figure 5.

Figure 5.

Modified rainfall intensity patterns: (a) first scenario; (b) second scenario

For the case study in SRM, four HRUs are defined (crop fields, fallow land, forest, and buildings), and their respective net rainfall values are calculated. The calculated yearly water balance for 2017 can be seen in Figure 6. This figure shows which amount of the total rainfall is available for the model (groundwater) and which is lost due to the different factors (runoff, canopy interception, soil evaporation, and transpiration). The forest HRU supplies the highest amount of available water for the model with 233.5 mm, whereas the fallow land only supplies 4.3 mm. For the crop area, the useful water amount comprises the groundwater (83.9 mm) and the plant's transpiration (287.1 mm), thus reducing the demand for irrigation.

Figure 6.

Steady state water balance in SRM, 2017

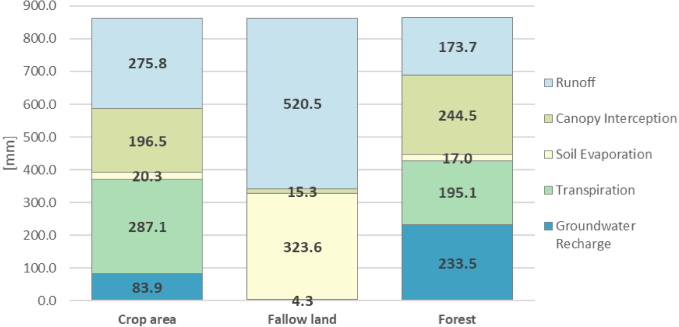
The forest HRU has greater canopy interception and transpiration losses than the fallow land, but in the fallow land, the losses through runoff and soil evaporation are significantly higher, which affects the percentage of groundwater recharge. This is a clear example of the value of trees and vegetation, which also increases the roughness of the ground, decreasing the surface runoff [23]. Considering the small water cycle and its long-term effects, by increasing the vegetation, it is possible to preserve and increase the local water availability [36].

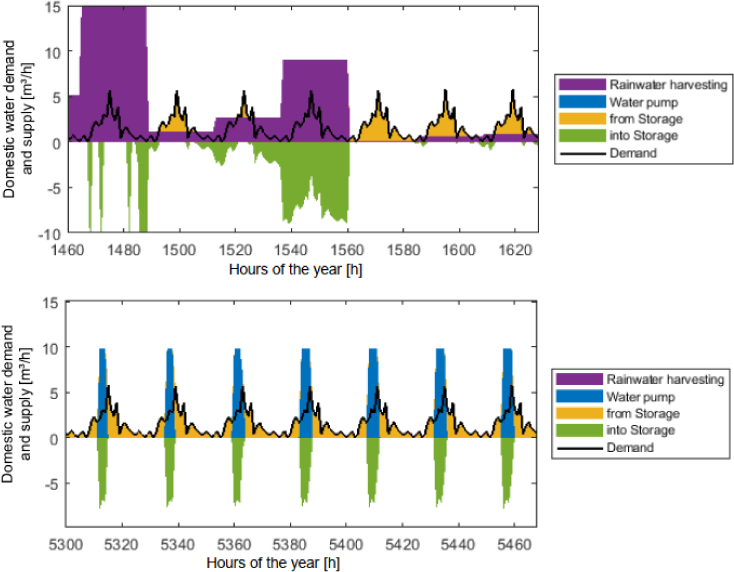
The water sources to cover the domestic demand are shown in Figure 7. During the rain season, the domestic water demand is supplied mainly through rainwater harvesting (purple) and the stored water (yellow) –– there is no need to use the pump. In the dry season, the demand is covered by a combination of a water pump (blue) and storage.

Figure 7.

Domestic water demand: rainy season (top) and dry season (bottom).

Figure 8.

Crop demand: rainy season (top) and dry season (bottom).

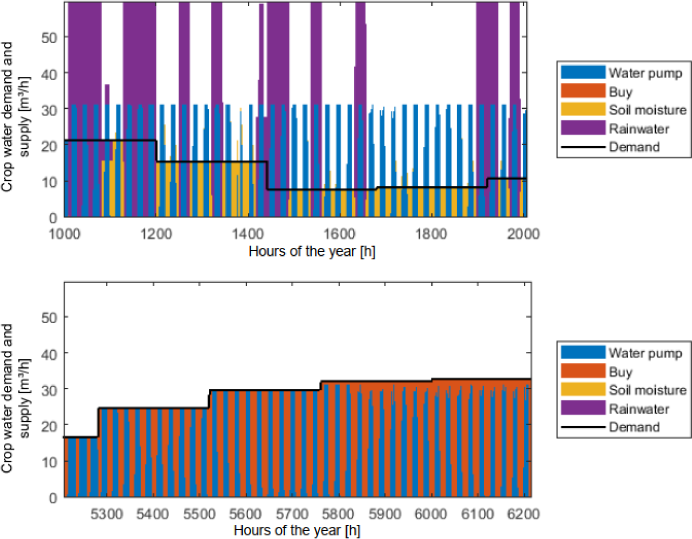
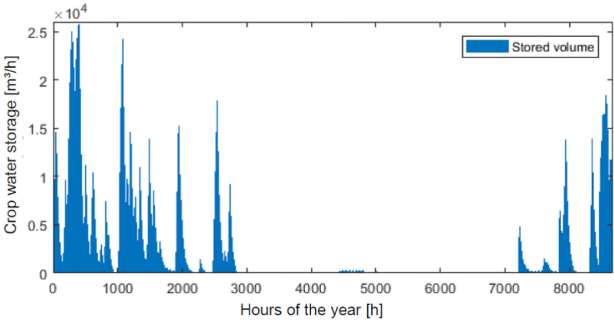
The water sources to cover the crop water demand can be seen in Figure 8. For the crop water demand, during the rainy season, a great amount is covered directly by the rainwater (purple) stored in the top soil (yellow). When the incoming rainfall exceeds the demand and the soil's retention capacity, this amount percolates into the lower ground layer, reaching the aquifer at some point. The stored water volume in the top-soil layer can be seen in Figure 9. As the operation costs for the solar pump (blue) are assumed negligible, it runs for some hours every day, even though it is not necessary.

In the dry season, the only local water source available is the solar pump (blue), which is not enough to cover the demand. Therefore, the model indicates that buying water (orange) is necessary to cover the deficits.

Figure 9.

Top Soil storage

The maximum pumping rate (max. Q) significantly impacts the model optimization. Figure 10 shows the water sources to cover the demand and their shares for each scenario with different pump rates. The water deficit (buy) increases for lower pumping rates, being 99,224 mm for a rate of 0.1 l/s and 0 mm for a rate of 2.5 l/s.

Figure 10.

Effects of maximum pumping rate on the coverage of the yearly water demand

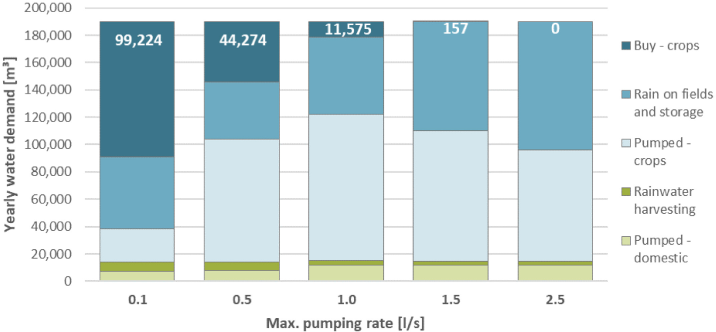
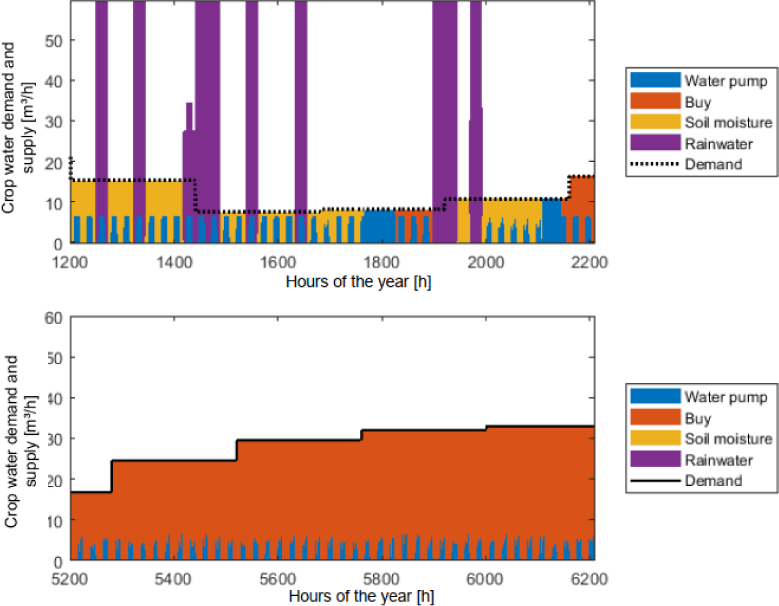
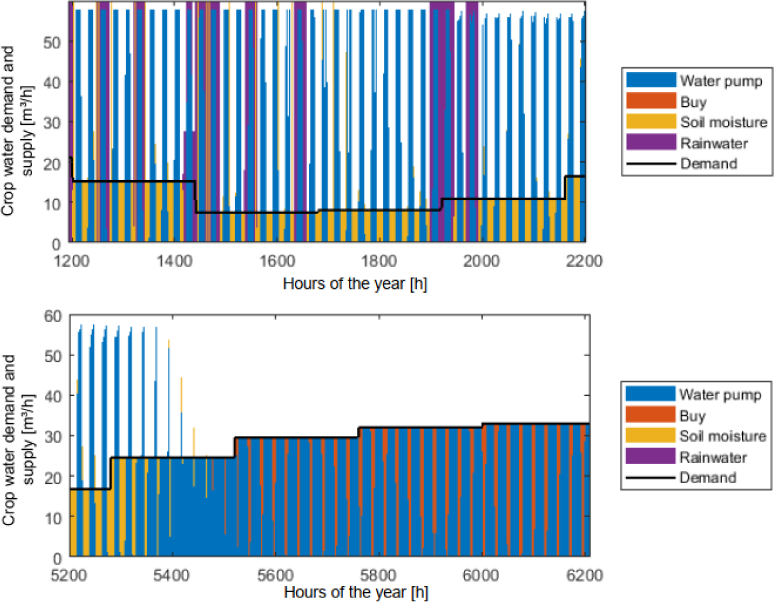
As can be seen in Figure 11 and Figure 12, the max. Q impacts the water deficit significantly, especially in the dry season. With a max. Q of 0.1 l/s, in the dry season, the available water (blue) is critically lower than the demand (the orange area represents the water deficit to cover the demand). A max. Q of 1 l/s improves the water supply significantly, but it is still insufficient to cover the demand in the dry season. For a pumping rate of 1.5 l/s, the water deficit represents 0.08 % of the demand. Figure 13 shows the amount of water deficit for each scenario.

Figure 11.

Max. Q = 0.1 l/s – Crop Water supply in the rainy season (top) and dry season (bottom)

Figure 12.

Max. Q = 1.0 l/s – Crop Water supply in the rainy season (top) and dry season (bottom)

Figure 13.

Water deficit for different max. Q values and K = 8E-09 m/s

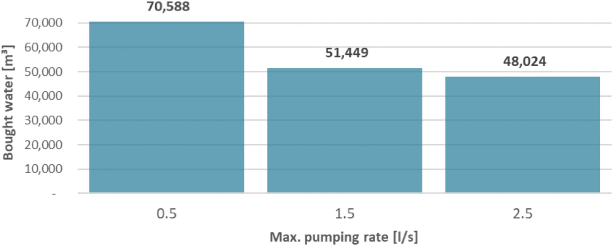
The parameter aquifer’s hydraulic conductivity has an impact on the water deficit. Even in scenarios where large maximum pumping rates are allowed, this parameter is limited by the aquifers properties. Therefore, the hydraulic conductivity has a greater importance for the optimization. This impact can be seen in Figure 14.

Figure 14.

Water deficit for different K values and max. Q = 54 m³/h

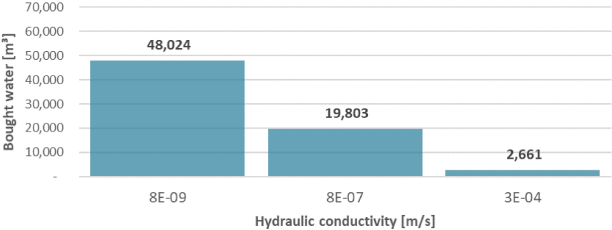
The parameter aquifer storage capacity has a significant impact on the optimization results. The percolation rate into the aquifer is 28.8 m³/(h ha) in the base scenario, compared to 0.3 m³/(h ha) in the worst-case scenario (decreased aquifer area and hydraulic conductivity), increasing the total water deficit. These results can be seen in Figure 15.

Figure 15.

Effect of aquifer size on the coverage of the yearly water demand

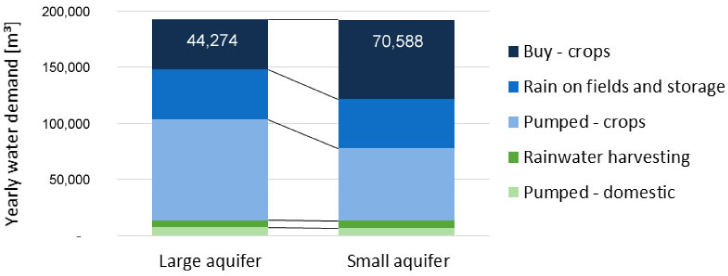
In the base scenario, the pumping rate is the limiting factor. In the worst-case scenario, the limiting factor is the groundwater storage volume. Thus, urbs administrates the available resources by implementing lower pumping rates. In the base scenario, the aquifer is frequently full (storage volume of 80,000 m³); in the worst-case scenario, the maximum volume stored is 697 m³ (right after the rainy season). The stored volume constantly decreases to empty by the dry season's end. In the "perfect" scenario for this case, the aquifer storage capacity must be big enough to store the groundwater needed in the dry season, and the pumping rate should be 2 l/s or higher.

Regarding land use, in SRM, from the 864 mm of total rainfall in the year 2017, the fallow land has a calculated yearly runoff of 520.5 mm (60.3 %) and the forest 173.7 mm (20.1 %). Whereas the forest area contributes to the yearly groundwater recharge, a calculated volume of 233.5 mm (27.0 %), the fallow land contributes only 4.3 mm (0.5 %). In the deforestation scenario (forest area decreases 73.7 %), the runoff volume increases 50 %, and the groundwater recharge decreases 67.2 %. In the afforestation scenario (forest area increases 66.5 %), the runoff volume decreases 44.2 %, and the groundwater recharge increases 60.6 %.

Nevertheless, the land use has little impact on the results of the model optimization. This may be due to the local rainfall patterns (intense rainfall events and long dry periods) with high runoff and evapotranspiration rates. In the rainy season, the available rainwater exceeds the demand and storage capacities, but at the end of the long dry season, all available water (from storage) is consumed. Considering the local natural conditions, it is clear that the rainwater storage capacities should be increased to cover the demand of the whole year.

With the rainfall intensity and pattern of SRM (short events of high intensity in the rainy season), even receiving a greater volume of rainwater would not decrease the water deficit significantly because the water availability in the dry period would not increase. Instead, a rainfall pattern with lower intensities and more rainy days would improve the local water availability, especially if the dry season is shortened. The effects of different rainfall intensities on the yearly water balance can be seen in Figure 16.

Figure 16.

Effect of rainfall intensity (52 mm, 32 mm, and 11 mm) and distribution patterns on the yearly water balance for the different HRUs

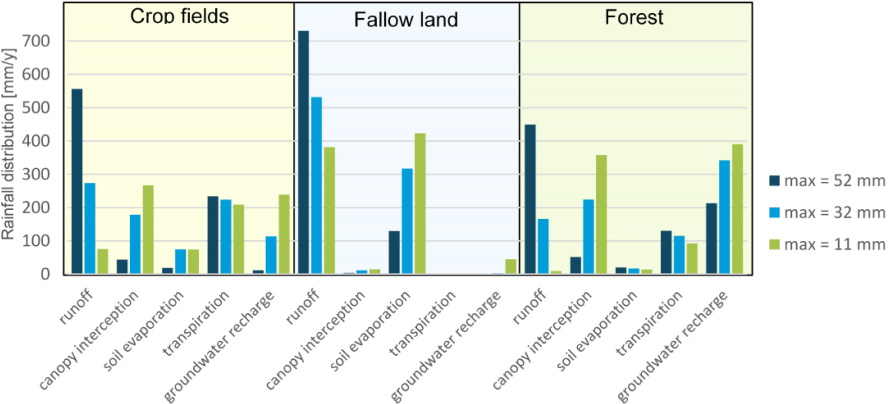
The rainfall intensity and pattern significantly impact the calculation of the net rainfall. In all HRUs, the runoff percentage rises with increasing rain intensities. Concerning the losses through canopy interception in the crop fields and the forest areas, these losses increase with more rainy days of lower intensities. The same applies to the losses through soil evaporation in the fallow land. In contrast, the groundwater recharge in the fallow land decreases for rain patterns of high intensities on less rainy days because losses through surface runoff are greater. Further on, in the rainy season, whereas a rain pattern of low intensities is enough to cover the whole demand, the rain pattern of high intensities and less rainy days presents water shortages. This deficit occurs because the rainfall volume at each rain event is greater than the volume that can be used or retained; thus, a smaller amount can be utilized.