Domestic hot water (DHW) availability is an essential comfort requirement in the hotel sector. After air conditioning, the DHW service is the second largest energy consumer, reaching values between 10% to 40% of total electricity consumption, which depends on the climatic conditions, hotel category and occupancy level [1]. Its production can be achieved through different technologies, including gas-fired, electricity, heat pump, solar systems, and power plants [2]. Its implementation depends on different factors, such as building characteristics, available equipment, loads properties and requirements, waste heat sources, availability and cost of water, electricity tariff, and climatological and operating parameters that ensure comfort and proper equipment operation.
The research in [3] analysed heat pump performance, using propane as a refrigerant to produce DHW at 60 °C in a hotel in Strasbourg. The modelling in TRNSYS helps to evaluate the heat pump operation from a specific model in combination with knowing its seasonal performance. Results showed that the control logic applied to the tank significantly influences energy consumption.
In [4], the COP is evaluated of the system, composed of two heat pumps producing hot water and thermal storage. The pumps have the equal capacity, one with CO2 refrigerant and the other with propane. As case studies, the paper considered the demand profiles of a school and a hospital in three different cities, proving that propane used as refrigerant allows energy savings to produce DHW in tropical climates and similar behaviour in cold climates.
An analysis carried out by [5] evaluates the feasibility of replacing conventional gas boilers with a heat pump and heat recovery to maximise DHW production. The research developed a model that includes a thermal and economic analysis as a base case analysing the influence of a wide set of parameters. The results showed that a system composed of a heat pump with heat recovery through a heat exchanger provides cost reduction; these results showed the advantages of replacing conventional gas boiler technologies. Also, [6] conducted a similar study to evaluate the impact of different operating conditions on a reversible heat pump for DHW production in cooling and heating mode. The authors concluded that using the liquid-vapour exchanger slightly negatively affects the system operation when there is no DHW production. However, when DHW production is the priority, it is reached a higher COP efficiency value.
A study developed by [7] on residential buildings in Italy proposes a numerical model that allows evaluation of the operation of reversible heat pumps with heat recovery and DHW production during summer. The model allows comparing this technology with the traditional chillers system and independent DHW production with traditional gas boilers, showing potential savings above 30%. Hengel [8] proposed a model to simulate a solar heat pump with heat recovery for DHW production in residential buildings with five different operating conditions. For the recovery strategy with a hydraulic circuit and own circulation pump, the efficiency increased by 5.3% while the electrical energy savings achieved a 5%. The other four strategies show annual electrical energy savings of about 4% compared with the systems without heat recovery. In both investigations, the results used dynamic simulations in TRNSYS to validate the strategies.
In [9], operating a Combined Cooling and Heating Power (CCHP) requires the development of a multi-objective optimisation model considering aspects such as energy, economy, and environment. In this system, heat recovery produces DHW derived from an absorption chiller and a heat pump, compared with a conventional system without condensing heat recovery. Results allow energy savings of around 5% and a decrease in CO2 emissions of 2.74%. Otherwise, [10] performed the thermodynamic simulation of a single-stage centrifugal chiller system combined with a heat exchanger placed between the compressor and the condenser. The system allows DHW and air conditioning supply simultaneously. The authors suggested that the thermodynamic simulation model in this combined system is important for optimising parameters such as the condensing and evaporating temperature in a domestic hot water flow rate and the size of a hot water storage tank.
A study developed for a hotel in Indonesia [11] reported that due to the operating regime of the air conditioning system, there are fluctuations regarding the hot water temperature value between 45 °C and 62 °C showing instability, reducing comfort levels. The DHW temperature value established for hotels according to the requirements in these facilities is 50 °C. The authors refer that one way to minimise fluctuations in hot water temperature is to use a thermal storage system.
In [12], assuming heat pump use in hot water supply systems for a residential building, the authors considered the optimum heat recovery during low potential heat utilisation and targets for heating and cooling capacities. The conclusion was that future works would focus on practical aspects such as optimal operation with higher thermal performance.
Several variables affect the chiller plant operation, including the water supply and return temperature, water flow, inlet and outlet temperature of the water/air flow in the condenser, and ambient temperature [13]. Typically, thermal system modelling uses nonlinear regression models based on the power consumption estimation and performance coefficient or thermodynamics and heat transfer equations, describing each component's processes. Usually, the equations do not consider all variables. These models have limited application in system operation because their performance is variable and subject to changes in operating conditions and some uncertainties [14]. Thus, models must dispense with evaluating thermodynamic properties that cannot be obtained directly from the system and instead use external measurable variables or manufacturer's data.
In addition, the production of hot water based on heat recovery, despite its wide use, has some disadvantages. These include the need for additional backup devices, mainly in the winter season, when the operation is at partial loads, so its operation must be carefully evaluated [15]. Primary energy sources generally used for this purpose are liquefied petroleum gas (LPG), diesel, fuel oil or electric power [16].
On the other hand, indirect hot water production occurs when the demand for air conditioning and hot water use do not coincide, so thermal storage is required. In these cases, storage tanks are installed to store and regulate the demand and supply of hot water for later consumption [17].
However, there is a lack of models that integrate an air conditioning/heat pump operation with the DHW production system [18]. Energy optimisation models also consider several process energy loss models to reduce leaks [19].
Based on the literature reviewed, they highlight only the benefits of the system energy savings based on an optimal plant design. There are variations in the thermal demand profiles for hotels. Air conditioning and hot water demands will vary according to the consumers' needs and uses. In this sense, fluctuations and peaks in demand at certain times destabilise the system, which affects its operational performance, evidencing instability in the set point temperature, with a reduction in comfort levels. Therefore, each installation requires a particularised analysis, identifying the factors that directly affect the integrated system.
This paper proposes a thermodynamic model of a central air-cooled chiller system with condensation heat recovery for DHW production with backup devices for water heating and thermal storage tanks. A hotel building located in a tropical climate is considered a reference case. The results can be useful for improving the performance of the integrated system to minimise the temperature instability during the day of the hot water supply.
The installation comprises two air-cooled screw chillers with condensation heat recovery, each connected in parallel. It has a tube and shell evaporator, expansion valve and R134a refrigerant as a working substance. The cooling occurs through air-cooled condensers with constant-speed fans, and the condensation heat is recovered to produce DHW through a desuperheater connected in series with each unit's condenser. Figure 1 shows a general system scheme.
General diagram system with heat recovery and thermal storage tanks for DHW
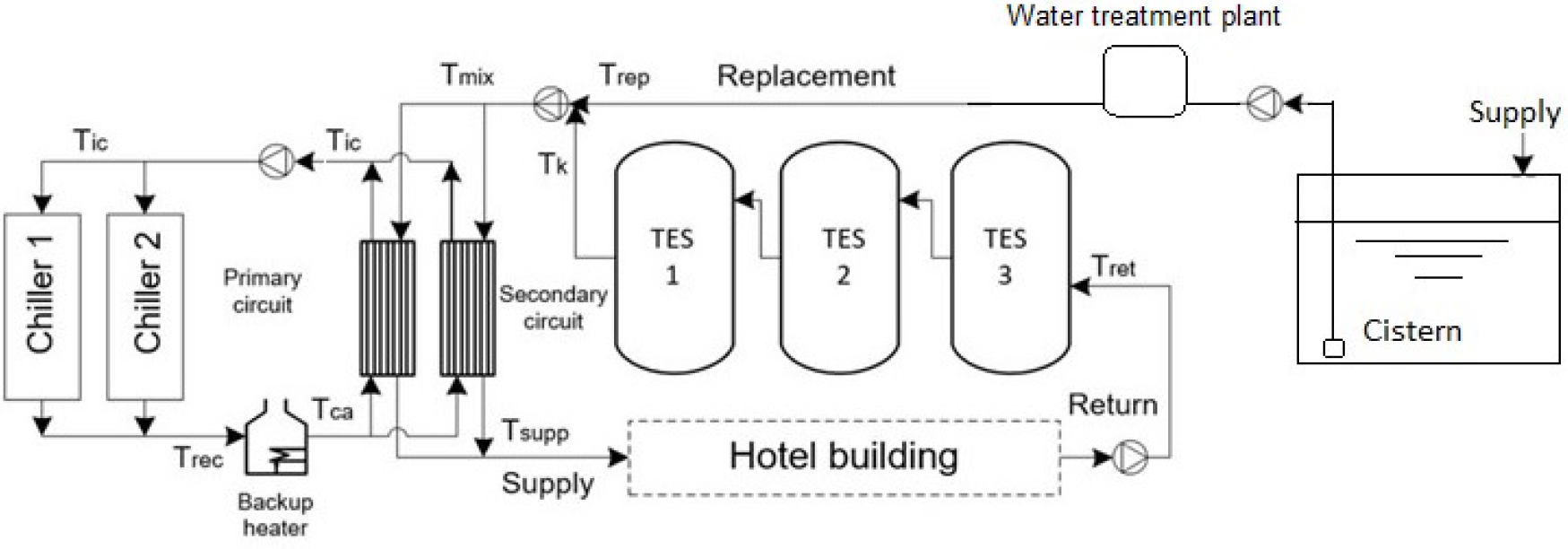
Depending on the thermal energy storage availability, one can achieve DHW production from condensation heat recovery directly or indirectly. The heat recovery circuit directly heats the water consumed in the direct system. In indirect production, thermal storage becomes necessary since the demand for air conditioning and DHW do not coincide. The storage tanks regulate the hot water demand and supply for later consumption [14]. Typical DHW systems in hotels with centralised air conditioning are composed of three circuits, comprising a group of pumps that operate 24 hours a day and boost the capacity depending on the demands of the hotel anytime. This system consumes 2% to 6% of the total electrical energy consumption [15]. Possible circuit arrangements are the following.
Primary hot water circuit (PHWC): while recirculating a certain volume of water, heat is partially recovered in the desuperheater before passing to the condensation process. This volume of water passes as a hot fluid through a plate heat exchanger until it returns to the heat recovery unit of the chillers. If the water temperature in the PHWC does not guarantee the set hot water temperature (60 °C), the water temperature in the PHWC increases automatically through a backup heater.
Secondary hot water circuit (SHWC): a volume of water circulates in counter-flow through the plate heat exchanger from the ambient temperature compensated in the DHW system, plus the volume of service water not consumed and returned. Once the water absorbs heat in the plate heat exchanger, storage tanks keep it.
Replacement circuit (RC): it promotes the hot water circulation through the service pipes network distributed throughout the hotel.
In these facilities, the heat available for reheating varies. Under certain operating conditions, it does not supply the DHW demand, which requires auxiliary heating and, therefore, additional energy consumption. The energy carriers commonly used for this purpose are liquefied petroleum gas (LPG), diesel, fuel oil and electric power [16].
Figure 2 summarises the main modelling steps in a block diagram with an energy model structure.
Block diagram with an energy model structure
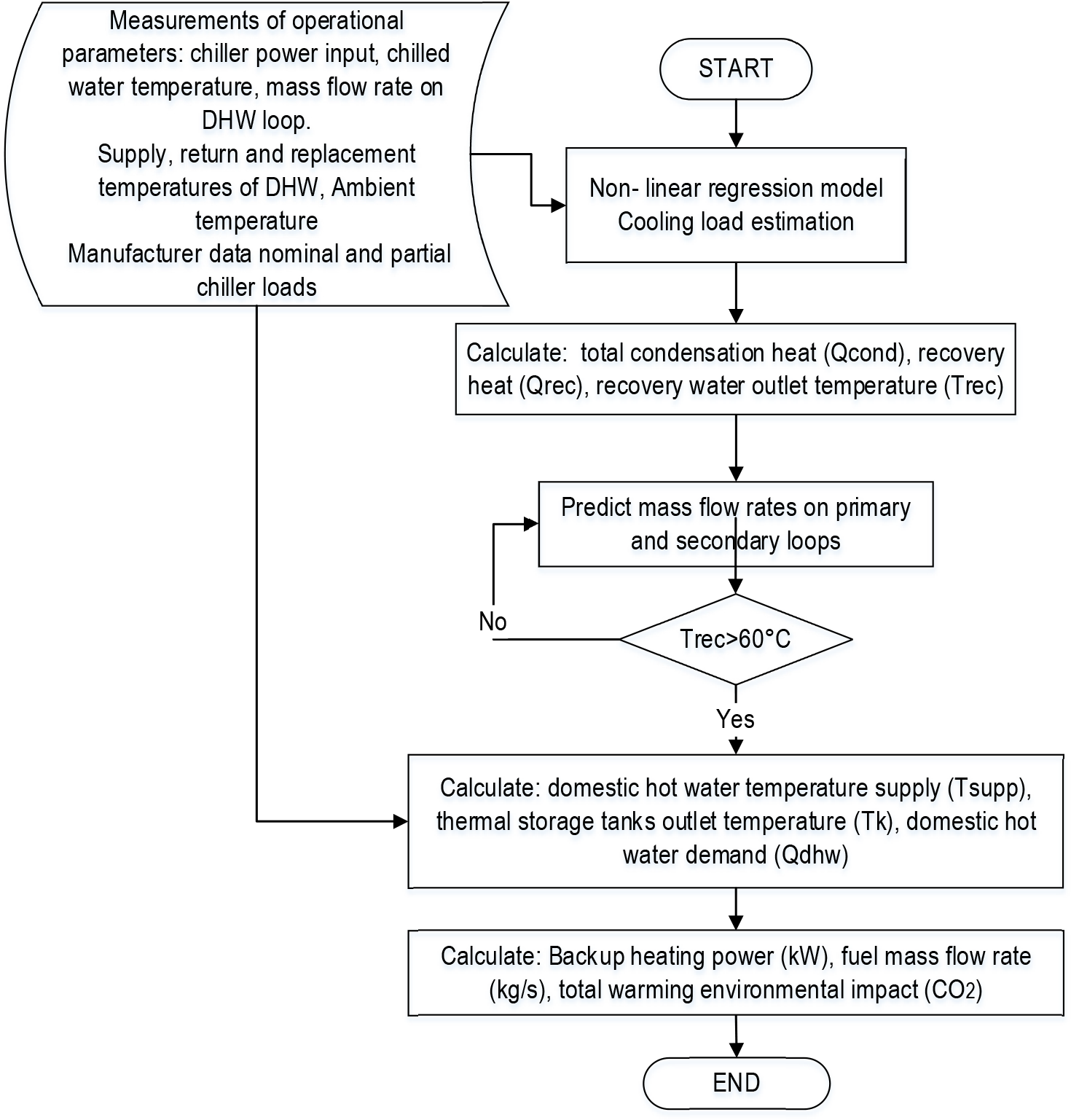
The following assumptions are adopted for the energy analysis of the hot water system with heat recovery:
A stationary operating condition exists.
Heat losses between heat exchangers and surroundings are negligible.
Temperature losses between supply and return hot water are about 5 °C.
The analysis neglects pressure drops in all heat exchangers.
There is no heat exchange between the chiller and its surroundings. This means that heat rejection is the sum of cooling capacity and compressor power.
The system works at a constant flow.
Regression methods used to fit experimental data in all science and engineering areas have been widely applied to study and simulate the behaviour of air conditioning systems [20]. As the hotel air conditioning load is a function of several variables, multiple linear regression (MLR) models are more appropriate than simple linear regression. A multiple linear regression model in statistics is a model that relates one or more Y variables to X explanatory variables using a functional relationship Y = F (X). When a data set is fitted to a mathematical model, errors are estimated between the actual data and those obtained with the fitted model.
While using the MLR, the number of variables is higher than two (dependent and independent variables), and the matrix representation can facilitate mathematical manipulations [21]. If one has k independent variables x1, x2, , xk and n observations y1, y2, , yn, the latter can be expressed as is presented in eq. (1):
(1)
This model represents n equations describing how the value of the response generates yn. Using matrix notation, eq. (1) can be written as follows:
(2)
The cooling load can be modelled as a linear combination of variables related to climatic conditions and operational variables, such as the chilled water temperature set point and the power demand of the chiller for those conditions. Understanding and interpreting this model is easy and does not require specialised software for its evaluation. Such a mathematical model provides a global and explicit formulation of the load behaviour.
Regression and correlation coefficients are determined for each combination of variables and functional relationships, considering a linear model. The advantage of linear models is their simplicity and ease of use; however, it is reported in the literature that nonlinear models, such as artificial neural networks, have better results.
A multiple nonlinear regression model is selected to estimate the cooling load profile. It uses operating and environmental parameters from a database that includes manufacturer's data, partial and nominal loads, and actual measurements of operating parameters. The inlet air temperature at the condenser is the ambient temperature, assuming an air condensing system. From the data provided by the manufacturer, it is possible to fit a model to determine the cooling load as the total electrical power function of the chiller (Ptot), the ambient temperature (Tamb) and the chilled water temperature (Tchw).
Curve fitting is applied to the available data using the ordinary least squares (OLS) method. The best fitting model is selected from the candidate models listed in Table 1, according to some error-boundaries fit metrics, such as adjusted R-squared, Lower Standard Error (LSE) and Mean Absolute Error (MAE).
Regression models list for cooling load estimation
| Model | Equation |
|---|---|
| Model 1 | Qe = a + bPtot |
| Model 2 | |
| Model 3 | |
| Model 4 | Qe = a + bPtot + cTchw + dTamb |
| Model 5 | Qe = a + bTchwTamb + cPtot |
| Model 6 | |
| Model 7 | |
| Model 8 | Qe = a + bPtot + cTamb + dTchw + ePtotTamb + fPtotTchw + gTambTchw |
Table 2 shows the metrics results where lower LSE and MAE values can be observed in the 8 model and a higher adjusted R2 value. This allows to conclude that it is the most adequate model and, therefore, it is selected as eq. (3). Table 3 summarises the adjusted parameters of the equation for each chiller.
Parameters selection for the regression model
| Models | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| LSE | 44.3865 | 43.184 | 41.6993 | 24.2597 | 42.7889 | 23.518 | 22.8972 | 1.77156 |
| MAE | 32.1898 | 31.6084 | 29.9111 | 17.6065 | 31.0842 | 18.0565 | 17.0355 | 1.27251 |
| R2ajusted | 92.7851 | 93.1707 | 93.6322 | 97.8447 | 93.2951 | 97.9745 | 98.08 | 99.9885 |
Regression models coefficients
| Coefficients | a | b | c | d | e | f | g |
|---|---|---|---|---|---|---|---|
| Chiller 1 | -156.61 | 6.1547 | 3.1990 | 5.5348 | 0.104851 | 0.0903932 | 0.20469 |
| Chiller 2 | -120.222 | 7.3770 | 2.7026 | 2.8551 | -0.13057 | 0.126092 | -0.157268 |
Therefore, the cooling load for each chiller can be determined by the following equation:
(3)
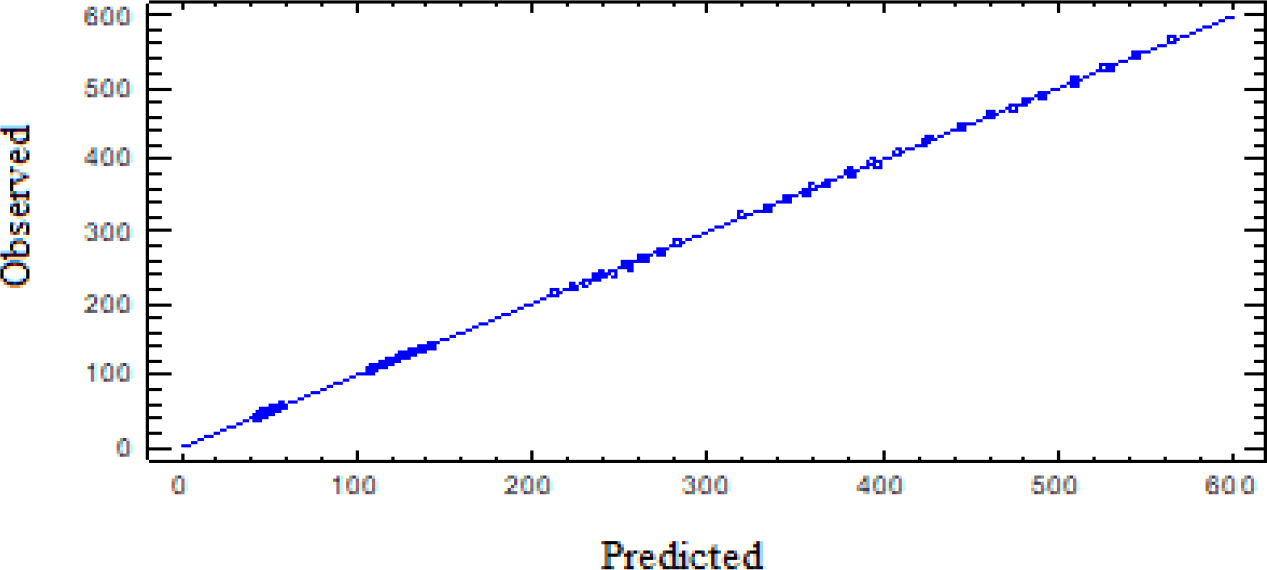
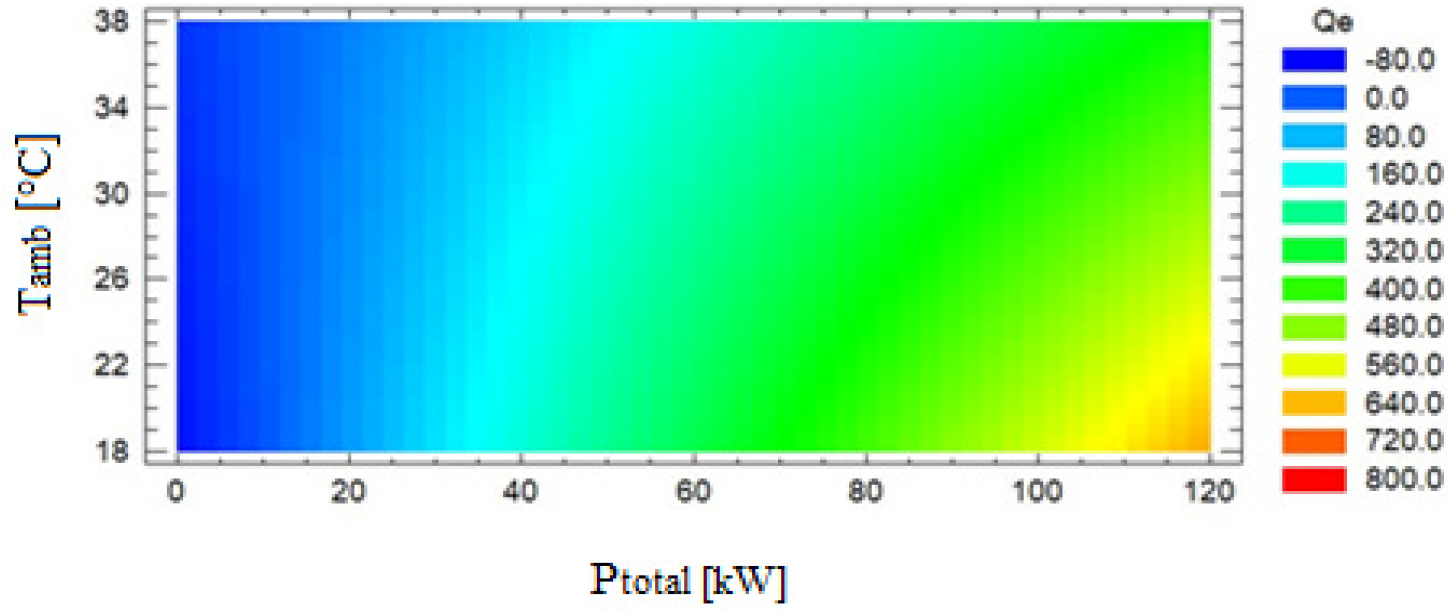
Figure 3 shows the observed values versus predicted, with a high correlation. Figure 4 depicts the estimated response surface, which, according to the model, represents the correlation between ambient temperature and total power versus the cooling load.
Correlation of observed versus predicted values of cooling capacity [kW]
Estimated response surface for the cooling load estimation model
The model does not consider the heat exchange between the chiller and the surroundings. Therefore, the total heat rejected in the condenser Qcond is the sum of the cooling capacity Qe and the compressor power Pcomp [22]:
(4)
Heat recovery within the refrigeration cycle is part of the total condensation process. The involved equipment unit is a refrigerant-water exchanger, which recovers heat from the refrigerant gas at the compressor discharge to heat DHW. The temperature at this point is relatively high, above 67 °C. The recovery process is in the sensible heat zone, representing about 25% of the total heat rejected in the condenser [6]. In addition, from the manufacturer's data, the recovery percentage is usually between 2025% of the total heat transfer in the condenser for most chiller manufacturers, while others declare up to 30%. The heat amount recovered by the chillers is estimated as:
(5)
It is possible to perform an energy balance in the primary hot water circuit to determine the heat in the heat recovery unit. Eq. (6) determines the outlet temperature of the consumed hot water (Tsupp) using the balance equation in the plate heat exchanger. The inlet temperature of the water in the primary circuit is 60 °C:
(6)
The energy balance equation determines the mixture temperature (Tmix) as a function of the replacement temperature and flow rate, water temperature in the tanks, and the return flow rate with the following equations:
(7)
(8)
The mixture temperature is thus:
(9)
The model considers the water's inlet and outlet volumetric flows, density, and heat capacity to analyse the thermal storage tanks. The water inside the tanks is well mixed due to the constant recirculation of the system. As the tanks are well insulated, the process is considered adiabatic. Eq. (10) gives the dynamic energy balance of the tank contents, which is a first-order ordinary linear differential equation expressing the relationship between the inlet and outlet temperature. In this equation, there is only one unknown value, T(t); while inlet temperature Ti(t) is an input variable:
(10)
The thermal demand for hot water is determined, considering the domestic hot water flow consumed and the temperature difference between the hot water supply and return flows:
(11)
The flow of hot water consumed is:
(12)
(13)
The measurements were monitored for a month using sensors and instruments listed in Table 4.
Sensors and instruments
| Variable | Instruments | Accuracy |
|---|---|---|
| Electric power, chiller 1 | Power analyzer MI 2392 PowerQ Plus | ± 0.5 + 0.1 A |
| Electric power, chiller 2 | Power analyzer EXTECH Model PQ3450 | ± 0.5 + 0.1 A |
| Supply hot water flow | Digital flow meter TDS-100 | ± 0.5 to 2.0% |
| Return hot water flow | Digital flow meter SITRANS FUP1010 | ± 0.5 to 2.0% |
| Hot water temperature | Digital Thermometer TESTO | ± 0.75 °C |
| Ambient temperature | RTD-PT100 | ± 0.02 °C |
The case study is Hotel Jagua by Meliá Hotels International, a four stars hotel with seven floors and 149 rooms near Cienfuegos Bay in Cuba. The main building has 136 rooms and 13 cabins, among other facilities like an event area, swimming pool, gym, and souvenir shops.
Cuba is a country with a tropical climate, with air conditioning needed for its buildings throughout the year, so it requires air conditioning systems. The centralised air conditioning system in the hotel comprises two air-cooled chillers, Frioclima CHAWT-1602 and Climaveneta FOCS 1702, with 505 kW and 363 kW of cooling capacity, respectively. The chilled water is supplied at 8.9 °C and returns at 11 °C in partial load operation.
In this study, a typical day of high hotel occupancy above 90% is selected in the peak tourist season in Cuba in November when ambient temperatures are lower. Measurements of hot water supply and return flow were made to estimate hot water consumption profile for a typical day, and DHW thermal demand was determined for 24 hours.
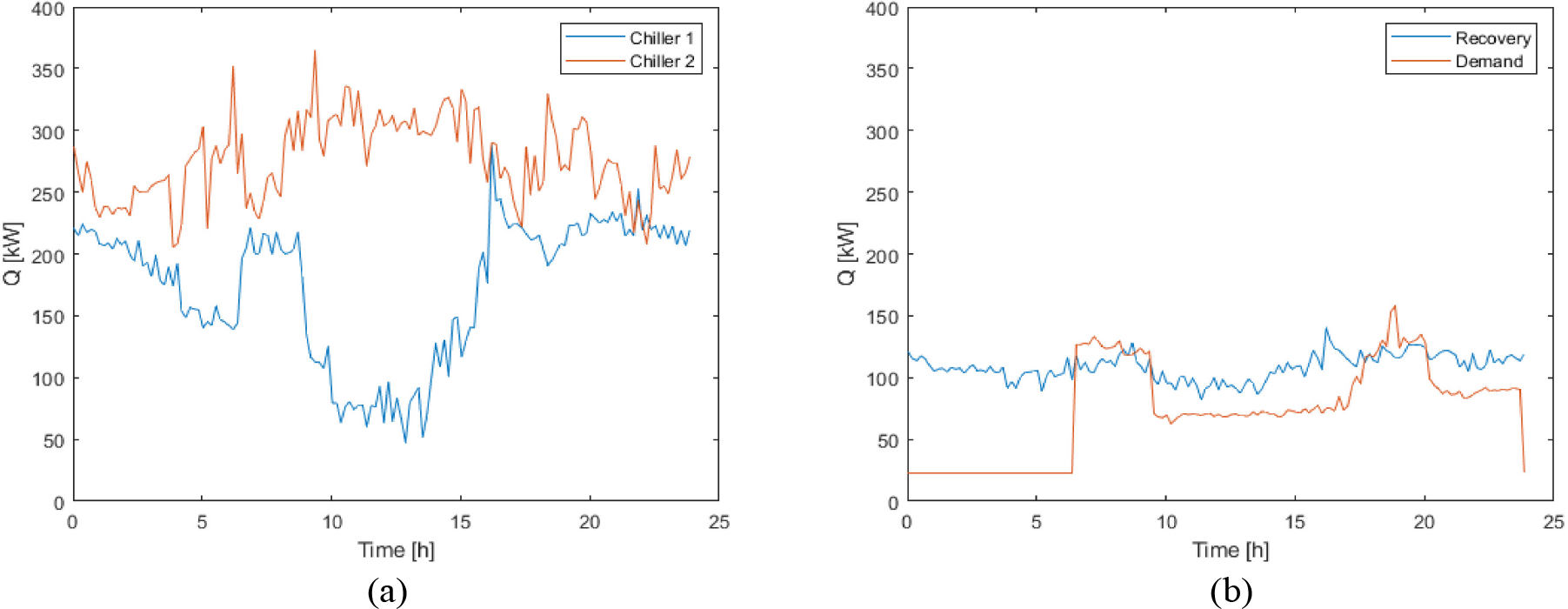
The model evaluates the energy performance of the system. The cooling demand for each chiller, the recovered heat potential, and the hot water demand profiles are shown in Figures 5a and Figure 5b. This consumption profile is typical in hotel facilities with basic hot water service, mainly for sanitary service in the rooms and the kitchen. The hot water from this system is considered medium temperature, not intended for laundry services, spas, or other facilities that some hotels may offer. Thermal demand for DHW shows maximum values found in two important peaks, first between 7:00 am to 9:00 am and the second between 6:00 pm to 10:00 pm, coinciding with the times of use of the hot water service. During the rest of the day, demand decreases to minimum values to guarantee the recirculation of hot water in the hydraulic system. Figure 5b shows that the response of the recovery system to the demand for hot water is not enough at times of high peak consumption. During these hours, backup devices are used to satisfy demand.
Cooling demand profile (a) and DHW thermal demand (b)
Modelling based on the energy balance of primary and secondary hot water loops allows obtaining the values of the inlet and outlet temperatures at the heat recovery unit (Tic and Trec, respectively), inlet and outlet to the plate heat exchangers, as well as the thermal storage tanks and supply temperatures.
Figure 6 shows the values of the temperatures in the hot water system when working in the recovery-only mode without auxiliary heating (Figure 6a) and with an auxiliary heater (Figure 6b). In both cases, there is a temperature increase in the early morning hours, when there is no hot water consumption, and therefore all the gained heat goes to the thermal storage tanks. Because the chillers work continuously at night to meet the air conditioning needs, heat is available to produce hot water. When this heat is not used, it is stored and recirculated.
Temperature profiles without auxiliary heating (a) and with auxiliary heating (b)
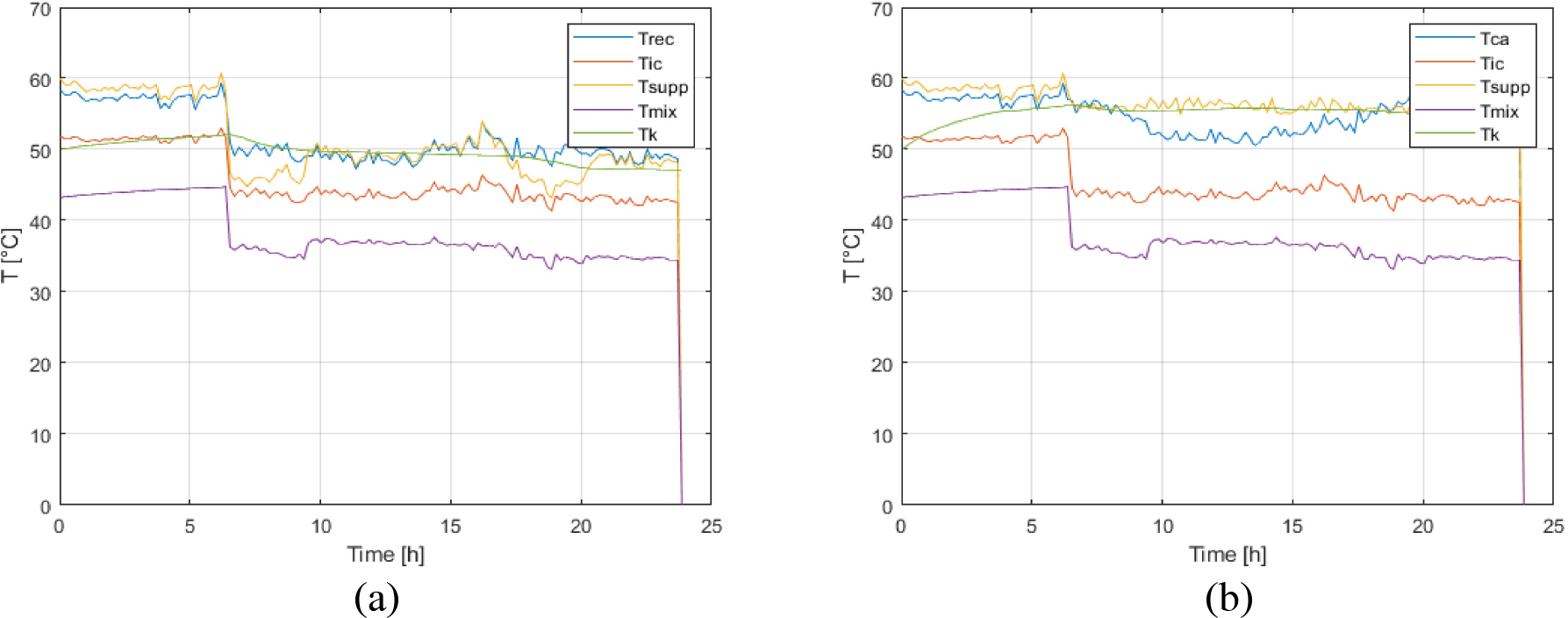
Performance of the hot water temperatures in the thermal storage tanks shows that, at an initial inlet temperature of 50 °C and no hot water consumption, it takes almost 7 hours of continuous operation of the chillers to reach 60 °C water temperature in the tanks. The temperature drops from the moment the consumption is started because of the continuous outflow of water from the tanks. The water temperature has a more stable behaviour, with the same tendency to decrease as soon as there is continuous consumption in the network. Remarking that these systems are constant flow, the heat gain in hot water circuits depends on the operation of the chillers. Heat recovery levels are low when the system works at partial loads in winter conditions. In this scenario, achieving a stable hot water temperature for thermal storage is difficult. Most of the time, the water does not reach 55 °C, so using auxiliary heating helps ensure that the hot water stored in the tanks maintains the set temperature. The above shows the operational deficiencies in the domestic hot water production system, which depends on the operation of the chillers, whose main function is to meet the cooling demand of the hotel facility.
In the first case, without auxiliary heating, the hot water temperature in the recovery (Trec) range is between 5055 °C, not reaching the required value (60 °C). Auxiliary heating is needed to ensure that the hot water is stored in the tanks at the set temperature after the thermal exchange with the secondary circuit. The temperature in the thermal storage tanks (Tk) drops from when consumption begins in the facility. It is observed that it does not establish itself throughout the day, reaching values as low as 47 °C during high-demand hours.
The greatest fluctuations occur in the supply temperature (Tsupp), which cannot stabilise due to the significant consumption peaks, failing to reach 50 °C when the established practice is to maintain it at around 55 °C ± 2°C. The other temperatures vary because they depend on the thermal exchange with those mentioned above, such as the temperature of the mixture (Tmix), which is the one that is replenished, plus the one stored in tanks that depends on consumption. However, in the system with auxiliary heating, the supply temperature stabilises around 55 °C, and the temperature in the tanks is maintained with minor variation. Of course, the temperature levels can increase to the required values, but this would require almost permanent use of auxiliary heating, as evidenced below.
In the hotel, the current backup device is a heater that works with liquefied petroleum gas. The operation of this heater is not automatic, so it depends on the operator's action to turn it on and off. Figure 7 shows results obtained from the evaluation of the system under real conditions, showing that the auxiliary heater takes part all the time to keep the system stable. Heater operation ensures that the hot water temperature does not drop below comfort levels and thus avoids instability in the hydraulic network; during high-demand hours, the needs are greater because the temperature must be increased by 5 °C in the morning peak and up to 8 °C at night. The hotel does not have a control strategy for the auxiliary heater. Depending on hot water consumption in the facility, the heater is turned on for about 2 hours in the morning and 2 hours in the afternoon, where the highest thermal demand peaks are concentrated.
Use of the backup heater to stabilise the domestic hot water temperature
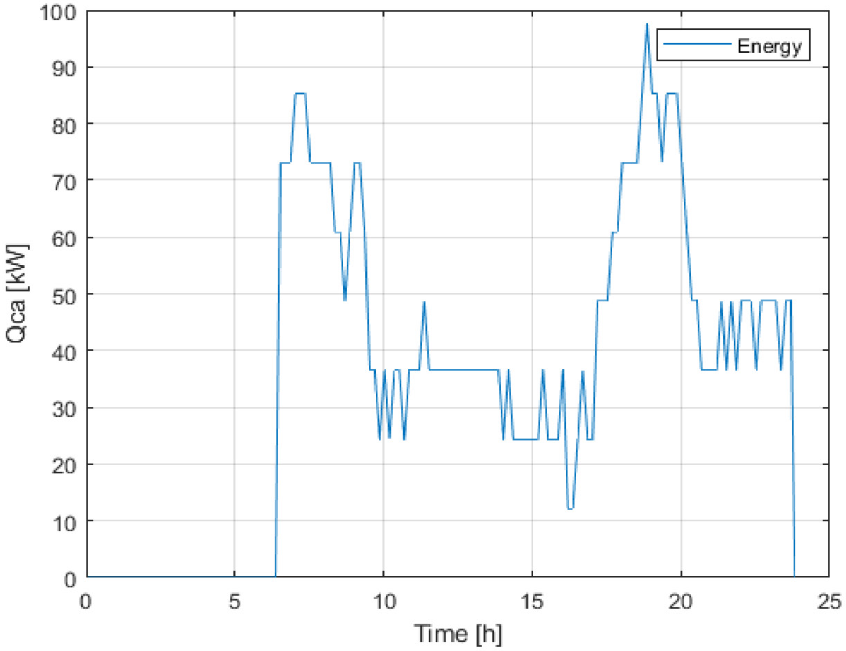
The results show that the system's current operation has insufficiencies that affect the stability of the required temperature values and the effectiveness of the heat exchange processes of the DHW production system. The current operation strategy does not allow for maintaining a constant hot water supply temperature. However, it achieves energy savings due to limited use of the auxiliary heater, concluding that this is not the best consideration. It is of great importance to study the variables that affect the behaviour of the temperatures to propose a strategy that allows for achieving stability in the hot water supply temperature and minimizing the fuel consumption used in the auxiliary heating.
Heat recovery is a favourable technique that saves energy for water heating. However, it does not fully cover the needs of hot water production required by a hotel in certain scenarios. Therefore, it does not completely guarantee the substitution of other energy sources used as a backup in the system when it does not reach the required temperature values.
The results of the energy analysis of the existing system compared to a traditional water heating system are shown in Table 5. The additional energy consumption for auxiliary heating is considered for the system with heat recovery and compared with a conventional gas-fired water heating system. Energy savings offered by heat recovery from the chiller is evident because they take advantage of their heat rejection thermal potential for producing another service, domestic hot water. Comparing the current system with a heat recovery chiller and auxiliary heating, an energy saving of 35,970 USD/year is achieved compared to a traditional water heating system. In addition, 253.4 t CO2/year is no longer emitted into the environment.
Energy results
| Unit | Heat recovery chiller + Auxiliary heating | Chiller + Conventional heating system | |
|---|---|---|---|
| Total chiller input power | [kW] | 172 | 172 |
| Chiller energy consumption | [kWh/day] | 3,440 | 3,440 |
| Cooling demand | [kW] | 376 | 376 |
| Water heating demand | [kW] | 185 | 185 |
| Heat recovery | [kW] | 137 | - |
| Heating system | [kW] | 48 | 185 |
| LPG consumption | [l/day] | 83.4 | 321.3 |
| Energy consumption | [kWh/day] | 1,054 | 4,061 |
| LPG Costs | [USD/year] | 12,610 | 48,580 |
| CO2 emissions | [t CO2/year] | 88.87 | 342.3 |
Heat recovery in DHW production is a useful technique for energy savings in this energy-intensive facility. However, results showed that auxiliary heating is required at partial load conditions because the system does not reach the temperature values for domestic hot water consumption.
Linear regression tools and thermodynamic models predict the system performance for a wide range of operating conditions with good accuracy. Operational behaviour is modelled from measurable external variables, such as electrical power, ambient temperature, chilled water temperature, hot water temperatures and mass flow rate, and the actual thermal potential profile available for DHW production during a typical day.
Compared with a traditional water heating system, the current system achieves fuel savings equivalent to 35,970 USD/year and saves 253.4 t CO2/year from being emitted into the environment.
However, in parallel with the advantages offered by this type of scheme, some insufficiencies affect the stability of the required temperature values. The effectiveness of heat transfer processes is decisive in overcoming these deficiencies; therefore, it is necessary to investigate operating strategies to optimise operating variables such as mass flows in hot water circuits.
- ,
A review of domestic hot water consumption profiles for application in systems and buildings energy performance analysis ,Renew. Sustain. Energy Rev. , Vol. 81 (May 2017),pp 15301547 , 2018, https://doi.org/https://doi.org/10.1016/j.rser.2017.05.229 - ,
Review of water-heating systems: General selection approach based on energy and environmental aspects ,Build. Environ. , Vol. 72 ,pp 259286 , 2014, https://doi.org/https://doi.org/10.1016/j.buildenv.2013.09.006 - ,
Évaluation de la performance saisonnière de systèmes de production deau chaude sanitaire fonctionnant au propane et de pompes à chaleur au CO2 ,Int. J. Refrig. , Vol. 74 ,pp 222237 , 2017, https://doi.org/https://doi.org/10.1016/j.ijrefrig.2016.09.026 - ,
A propane water-to-water heat pump booster for sanitary hot water production: Seasonal performance analysis of a new solution optimizing COP ,Int. J. Refrig. , Vol. 51 ,pp 5969 , 2015, https://doi.org/https://doi.org/10.1016/j.ijrefrig.2014.12.008 - ,
Optimal sizing of a heat pump booster for sanitary hot water production to maximize benefit for the substitution of gas boilers ,Energy , Vol. 127 ,pp 558570 , 2017, https://doi.org/https://doi.org/10.1016/j.energy.2017.03.131 - ,
Analysis of the impact of different operating conditions on the performance of a reversible heat pump with domestic hot water production ,Int. J. Refrig. , Vol. 86 ,pp 282291 , 2018, https://doi.org/https://doi.org/10.1016/j.ijrefrig.2017.11.005 - ,
Dynamic simulation during summer of a reversible multi-function heat pump with condensation-heat recovery ,Appl. Therm. Eng. , Vol. 116 ,pp 126133 , 2017, https://doi.org/https://doi.org/10.1016/j.applthermaleng.2017.01.066 - ,
Performance analysis of a heat pump with desuperheater for residential buildings using different control and implementation strategies ,Appl. Therm. Eng. , Vol. 105 ,pp 256265 , 2016, https://doi.org/https://doi.org/10.1016/j.applthermaleng.2016.05.110 - ,
Operation optimization for combined cooling, heating, and power system with condensation heat recovery ,Appl. Energy , Vol. 230 (August),pp 305316 , 2018, https://doi.org/https://doi.org/10.1016/j.apenergy.2018.08.101 - ,
Thermodynamic simulation of condensation heat recovery characteristics of a single stage centrifugal chiller in a hotel ,Appl. Energy , Vol. 91 (1),pp 326333 , 2012, https://doi.org/https://doi.org/10.1016/j.apenergy.2011.08.007 - ,
Minimizing temperature instability of heat recovery hot water system utilizing optimized thermal energy storage ,J. Phys. Conf. Ser. , Vol. 953 (1), 2018, https://doi.org/https://doi.org/10.1088/1742-6596/953/1/012113 - ,
Possibility of heat pump use in hot water supply systems ,J. Sustain. Dev. Energy, Water Environ. Syst. , Vol. 4 (3),pp 203215 , 2016, https://doi.org/https://doi.org/10.13044/j.sdewes.2016.04.0017 - ,
A practical approach to chiller plants optimisation ,Energy Build. , Vol. 169 ,pp 332343 , 2018, https://doi.org/https://doi.org/10.1016/j.enbuild.2018.03.076 - ,
Empirical Correlation Based Models for Estimation of Air Cooled and Water Cooled Condensers Performance ,Energy Procedia , Vol. 109 (November 2016),pp 293305 , 2017, https://doi.org/https://doi.org/10.1016/j.egypro.2017.03.070 - ,
Integrated HVAC and DHW production systems for Zero Energy Buildings ,Renew. Sustain. Energy Rev. , Vol. 40 ,pp 515541 , 2014, https://doi.org/https://doi.org/10.1016/j.rser.2014.07.193 - ,
Energy-efficient and -economic technologies for air conditioning with vapor compression refrigeration: A comprehensive review ,Appl. Energy , Vol. 232 (September),pp 157186 , 2018, https://doi.org/https://doi.org/10.1016/j.apenergy.2018.09.067 - ,
Performance of Newly Developed Integrated Space COnditioning and Domestic Water Heating Device ,J. Energy Environ. , Vol. 3 (1),pp 23.27 , 2011https://journal.uniten.edu.my/index.php/jee/article/view/116 - ,
Operation analysis and performance prediction for a GSHP system compounded with domestic hot water (DHW) system ,Energy Build. , Vol. 119 ,pp 153163 , 2016, https://doi.org/https://doi.org/10.1016/j.enbuild.2016.03.024 - ,
Optimización enegética de bombas centrífugas a través de un análisis paramétrico en CFD y modelos de pérdida de energía ,Inge Cuc , Vol. 16 (1),pp 1.21 , 2020, https://doi.org/https://doi.org/10.17981/ingecuc.16.1.2020.01 - ,
Methodology for the preparation and selection of black box mathematical models for the energy simulation of screw type chillers Metodología para la confección y selección de modelos matemáticos de caja negra para la simulación energética de enfriadoras ti , 2020 - , , Probabilidad y estadística para Ingeniería y ciencias, 2012
- ,
Improved energy performance of air-cooled chiller system with mist pre-cooling Mist improvement on air-cooled chillers ,Appl. Therm. Eng. , Vol. 31 (4),pp 537544 , 2011, https://doi.org/https://doi.org/10.1016/j.applthermaleng.2010.10.012




