Nowadays, with the rapid development of renewable energy technology and flexibility required in modern power systems. The integration of renewable energy sources (RESs) into the existing distribution network has become the focus of several current studies. Microgrid (MG) seems to be an effective and promising technology for penetration of RESs. A MG can be described as an integrated energy system consisting of distributed energy resources (DERs), battery storage system (BSS), and loads. It can operate either in grid connected mode through purchasing or selling power from orto the main grid [1], or in standalone operation mode in case of emergencies or remote areas.

A typical MG generally incorporates an energy management system (EMS) as a crucial component for power management optimization, to improve power supply quality, and efficient control of MG operations.

The multi-objective optimization dispatch (MOOD) problem and operation control of MG have been addressed in several studies. And various objective functions with constraints are developed.

The authors in [2] propose the design and implementation of a fuzzy logic energy management system for a polygeneration MG.To show the superior performance of the proposed approach, a comparison with an ON/OFF management strategy has been discussed. The obtained simulation results reveal that the fuzzy logic approach can efficiently manage the overall energy of the MG system and provides a considerable decrease in the size of the installed components.Having already demonstrated its relevance for dealing with complex challenges in MG system, Vivas et al.propose in [3] a multi-objective fuzzy logic based EMS for energy management and operation control of a typical MG. In addition to responding to the load demand, the developed fuzzy logic controllerguarantees a considerable cost saving and it can also prolong the lifespan of the installed devices (li-ion battery bank and hydrogen system). The research in [4] also confirms the potential of the fuzzy logicfor energy management of a standalone hybrid renewable energy system over 25 years. The results show that the developed EMS optimizes the utilization costs, also it guaranteesan extended lifetime of the battery and hydrogen system.

In Nwulu et al. [5], the implementation of a novel control approach to optimize the dynamic economic and emission dispatch (DEED) problem has been discussed, by considering the integration of a game theory based demand response (DR) program into the optimization problem. The obtained results indicate the practical benefits of the developed model compared with independent optimization of DR or DEED. Aghajani et al. [6] proposed a multi-objective particle swarm optimization (MOPSO) method for day-ahead energy management, considering operation cost and emission rate as objective functions.The achieved results are compared with non-dominated sorting genetic algorithm II (NSGA-II), showing the superior performance of the proposed method. Murty et al. [7] propose a novel approach for economic-environmental optimization dispatch. Beside the technical constraints consideration and the integration of DR in the optimization problem, the authors provide a fuzzy interference system for optimal charging/discharging of BSS. The global criterion method is used to formulate the multi-objective optimization problem (MOOP), then the performance of the proposed methodology is compared with other heuristic optimization techniques.

Nowadays, a number of novels and hybrid evolutionary and heuristic optimization algorithms have been introduced to handle the MOOD problem. In Wang et al. [8], a novel hybrid multi-objective fireworks algorithm with gravitational search operator (MFAGSO) has been proposed to solve the operation cost and pollutant emission as competing objectives inside a typical grid connected MG for 24-h period. An improved strength Pareto evolutionary algorithm (ISPEA2) [9] is also suggested to solve the MOOD problem. Considering the fuel cost and emission as two objective functions to be minimized. Furthermore, a fuzzy based membership function is employed to extract the best compromise solution from the obtained Pareto optimal set. The superiority of the proposed method is verified by comparing the results obtained using the ISPEA2 with those of other methods employed in the literature. Hou et al. [10] propose the implementation ofmulti-objective seeker optimization algorithm (MSOA) with a decision making based on fuzzy membership function to obtain the Pareto optimal set and to find the best compromise solution. The multi-objective economic dispatching model includes the economy of MG, the efficiency of photovoltaic system utilization as well as the security of the connect-line between MG and main grid.

The ant lion optimizer (ALO) is a newly developed algorithm by Seyedali Mirjalili [11] that has been successfully applied forhandlingthe MOOD problem in MG power system [12]. Van et al. [13] propose the implementation of ALO algorithm for handling the optimal economic load dispatch (ELD) problem. The authors consider challenging constraints such as spinning reserve constraint, ramp rate limits, prohibited operating zones of generating units. Three case studies have been investigated. The obtained results are compared with other heuristic methods to prove the efficacy of ALO method. In [14], ALO was used to solve the ELD problem, while considering the application of DR as virtual power plant in the formulated optimization problem. In this study, the overall operating cost, system losses and emission levels are considered as objective functions to be minimized. Then, the performance of ALO was verified by a comparative study with particle swarm optimization (PSO) and artificial immune system (AIS). The authors in [15] also suggest the use of ALO method to deal with the multi-objective of both total operating cost and total pollutant emission. Two scenarios are proposed: the first one is operating all the installed DERs and main grid within specified limits, while the second scenario is operating both RESs at their rated powers. The obtained simulation results were compared with those provided using well-known heuristic optimization algorithms like PSO, grey wolf optimizer (GWO) method and whale optimization algorithm (WOA). They also prove that the proposed ALO algorithm can significantly minimize the operating cost and emission in the studied MG while satisfying the specified constraints.

Previous works rarely consider the power loss of conversion devices in the formulated optimization problem. According to [16], this power loss may vary between 2% and 16% of conversion power. Therefore, in this work it is considered as one of the objective functions to be minimized.

This paper aims at day-ahead optimizing dispatch and coordinated control of a MG power system. The developed EMS is designed to operate in two-level architecture. The highest layer with the function of the control and optimal charging - discharging power of the BSS. Whilethe lower layer is implemented in order to solve the multi-objective optimization dispatch problem. The formulated problem involves the minimizing of three contradictory objective functions representing: the overall operating cost, the emissions level of (NO_x, SO₂, CO₂), and the power loss of the conversion devices, taking into account the technical constraints of the system [17]. Ant lion optimizer algorithm is selected for handling the MOOD problem. To validate the robustness and efficiency of the proposed approach, the performance of ALO is compared with other well-known heuristic algorithms, including artificial bee colony (ABC) [18], WOA [19] and PSO technique.

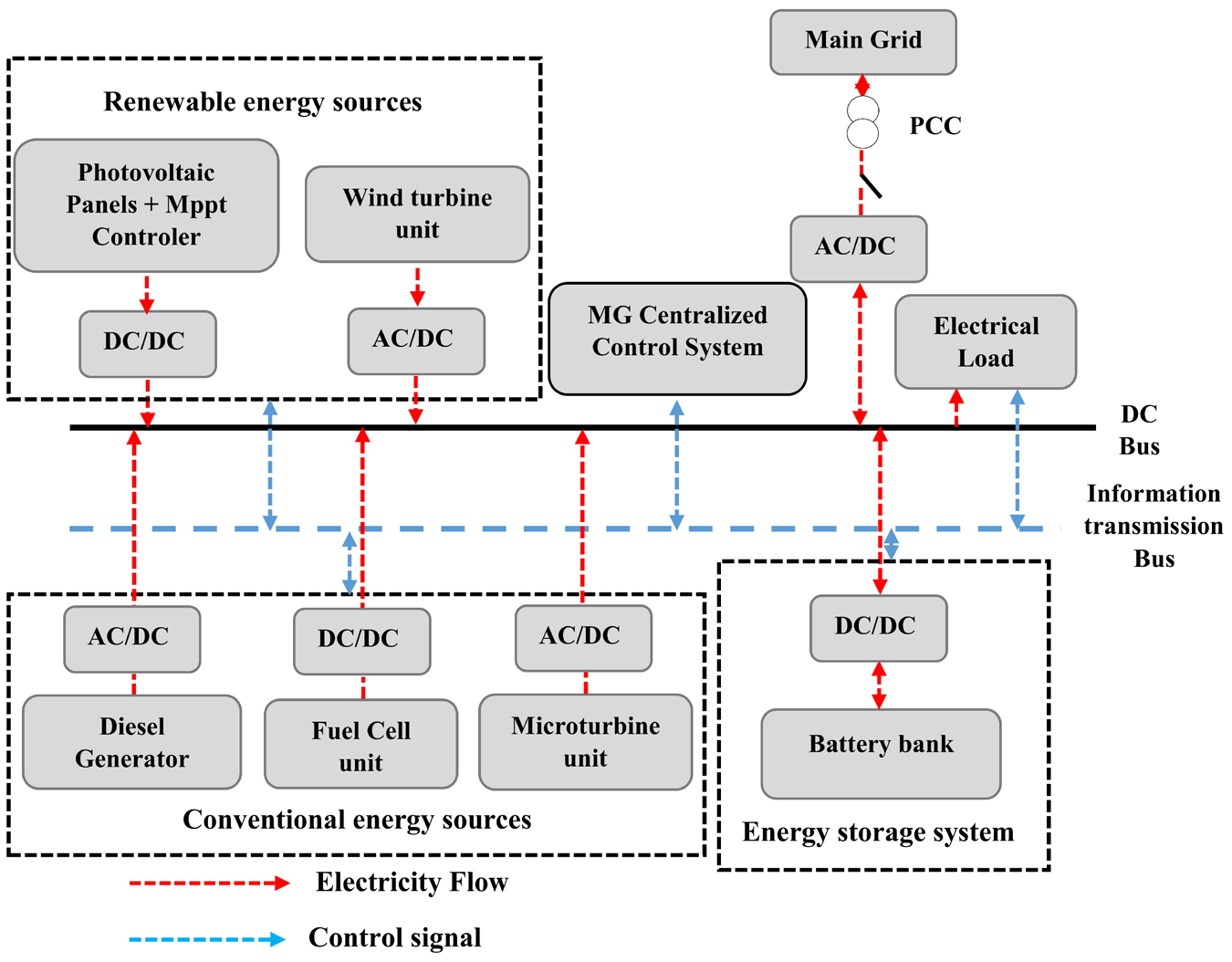
The configuration of the proposed MG power system in grid connected mode is shown in Figure 1. In this system three different energy sources are considered: renewable energy sources, conventional energy sources (CESs), and energy storage system (ESS). The RESs combine photovoltaic (PV) panels with wind turbine (WT) unit, while CESs contain a diesel generator (DG), a fuel cell (FC), and a micro-turbine (MT). Due to the flexible charging-discharging characteristics of BSS, it is used as a backup to maintain power balance and to improve the reliability of the system [20]. The MG is connected to the main grid through a point of common coupling (PCC). While the interconnection to the common DC bus is ensured through power conversion devices. All the components are connected through an information bus to a centralized EMS developed for ensuring secure, reliable, and economical operation of the MG system [21].

Power generation resources

The PV and WT power outputs are not available all the time, and their performance is affected by weather conditions. In order to ensure a continuous availability of power and reduce the operating cost of the system a battery bank is used as a backup.

The mathematical modelling of the power generated from both RESs and battery storage system parameters constrains are detailed hereafter.

Figure 1

Configuration of the studied grid connected microgrid (MG)

PV power system.

The power generated from the PV unit is primarily depends on the incident irradiance G and cell temperature T. It is expressed as follows [17], [22], [23]:

$P_{\text{PV}}=F_{\text{PV}}\times P_{\text{PV,R}}\times \frac{G}{G_{\text{STC}}}[1+{\alpha }_{\text{T}}(T-T_{\text{STC}})]$ (1)

where T_STC and G_STC represent, respectively the temperature and irradiance under standard test conditions, and α_T is the temperature coefficient.

WT power system.

Based on the wind speed V and the rated power P_WT,R of WT unit. The output power P_WT can be calculated as follows given as [22], [24], [25]:

$\{\begin{array}{c}P{}_{\text{WT}}=0;V<V_{\text{CI}}\text{or}V\text{>}{V}_{\text{CO}}\\ P_{\text{WT}}=P_{\text{WT,R}}\left(\frac{V^3-V_{\text{CI}}^3}{V_{\text{R}}^3-V_{\text{CI}}^3}\right);V_{\text{CI}}<V<V_{\text{R}}\\ P_{\text{WT}}=P_{\text{WT,R}};V_{\text{R}}<V<V_{\text{CO}}\end{array}$ (2)

where, V_CI, V_CO, V_R indicate the cut-in, cut-out and rated wind speed, respectively.

It is to be noted that both PV panels and WT modules are assumed to be equipped with a maximum power point tracking (MPPT) system in order to increase the generation from RESs, making it beneficial from an economic point of view.

Battery storage system.

In the studied MG system, a lithium-ion battery bank of 240 V, 400 Ah is chosen as ESS. This technology is characterized by its larger storage capacity, high efficiency, fast charging capability, prolonged life cycle, and high-energy density [26]. State of charge (SoC) of the battery is considered as an important parameter to be controlled. The variation of the battery SoC with the charging, discharging process is expressed by eq. (3) given as [26], [27]:

${\text{SoC}}_{\text{t}}={\text{SoC}}_0+\frac{1}{Q}{\displaystyle \underset{t_{\text{o}}}{\overset{t_{\text{f}}}{\int }}idt}$ (3)

where ${\displaystyle {\int }_{t_{\text{o}}}^{t_{\text{f}}}idt}$ and Q represent respectively, the instantaneous and total capacity of the battery bank in Ah.

In order to extend the cycle life of the BSS, monitoring its SoC is needed to prevent it from any overcharging or under-discharging. Thus the battery's SoC is constrained between the minimum and maximum limits given as follows [22], [28]:

${\text{SoC}}_{\text{Min}}\le {\text{SoC}}_{\text{t}}\le {\text{SoC}}_{\text{Max}}$ (4)

where SoC_Min and SoC_Max are the lower and upper limits of the battery SoC, respectively.

The output power of the battery storage at time t should should be maintained within the minimum and maximum limits as follows [29]:

$P_{{\text{BSS}}_{\text{min}}}\le P_{\text{BSS}}(t)\le P_{{\text{BSS}}_{\text{max}}}$ (5)

It should be noticed that in each time step, the BSS must be in one operating mode only. Positive value of P_BSS corresponds to a battery in discharging mode, negative value refers to the charging mode. Stop mode corresponds to a battery generation equal to zero whenever the battery SoC is less than 10%, or in case when the battery reaches a maximum SoC (SoC_Max=80%) and the supply of both RESs match the DC load demand.

In this section, the mathematical formulation of the MOOD problem, is to minimize simultaneously the objective functions F₁, F₂ and F₃ subject to equality and inequality constraints. The decision variable includes the power of dispatchable sources and the exchanged power with the main grid.

Objective functions

In the studied MG, three conflicting objective functions are considered to be minimized: The operating cost of MG system is defined as the first objective function, followed by the pollutant gas emissions cost of nitrogen oxide, sulfur dioxide and carbon dioxide (NO_x, SO₂ and CO₂) respectively, and the third objective function is the power loss cost of the conversion devices.

The linear additivity of the objective functions is not applicable to solve the MOOD problem [30]. Therefore, the price penalty factor (PPF) is considered to transform the multi-objective optimization problem into a single-objective problem. Then a weighting approach based on the weighted sum method is applied to find the Pareto front solutions [31].

Mathematically the MOOD problem is formulated by eq. (6) given as [32]:

$\min O{F}_{\text{MG}}{\displaystyle {\sum }_{t=1}^{24}{\omega }_1{F}_1+{\omega }_2{F}_2+{\omega }_3{F}_3}$ (6)

where, ω_i is the weight coefficient related to the objective function F_i.

Operating cost function.

The primary concern of the studied MG system is to minimize the operating cost. It incorporates four terms representing the fuel cost of generators, start-up cost, operation & maintenance (O&M) cost, and exchanged power cost with the main grid, given as [22], [23], [33]-[35]:

$F_1={\displaystyle \sum _{i=1}^N\{C{F}_i(P_i)+O{M}_i(P_i)+ST{C}_i\}}+(CPE-RSE)$ (7)

• Fuel cost of diesel generator

The fuel cost consumed by the diesel generator is expressed as a quadratic function of the active power given as [22], [23], [28], [33], [35]:

$C{F}_{\text{DG}}(P_{\text{DG}}(t))={\alpha }_{\text{DG}}+{\beta }_{\text{DG}}{P}_{\text{DG}}(t)+{\gamma }_{\text{DG}}{P}_{\text{DG}}^2(t)$ (8)

where, α_DG, β_DG, γ_DG are cost coefficients of the DG.

• Fuel or gas cost of fuel cell and micro-turbine

The cost of the fuel or natural gas consumed by the FC or the MT units, respectively is calculated as follows [34], [35]:

$C{F}_i(P_i(t))=C_i{\displaystyle \sum _i\frac{P_i}{{\eta }_i}}$ (9)

where C_i is the fuel or natural gas price of generating unit i (FC or MT), and η_i represent the efficiency of the generating unit i.

It is worth mentioning that by substituting the efficiency curve, which associates the efficiency to the generated power in eq. (9), the fuel or natural gas cost consumed by FC or MT unit can be approximated as a quadratic function of the actual output power, similar to the mathematical model of DG but with different cost coefficients [35].

• Operation and maintenance cost

The O&M cost of each conventional energy source is expressed as a linear function of the actual output power P_i given as [22], [34]:

$O{M}_i={\displaystyle \sum _{i=1}^N{K}_{{\text{OM}}_i}{P}_i}$ (10)

where K_OMi is O&M cost coefficient of each generating unit i.

• Start-up cost

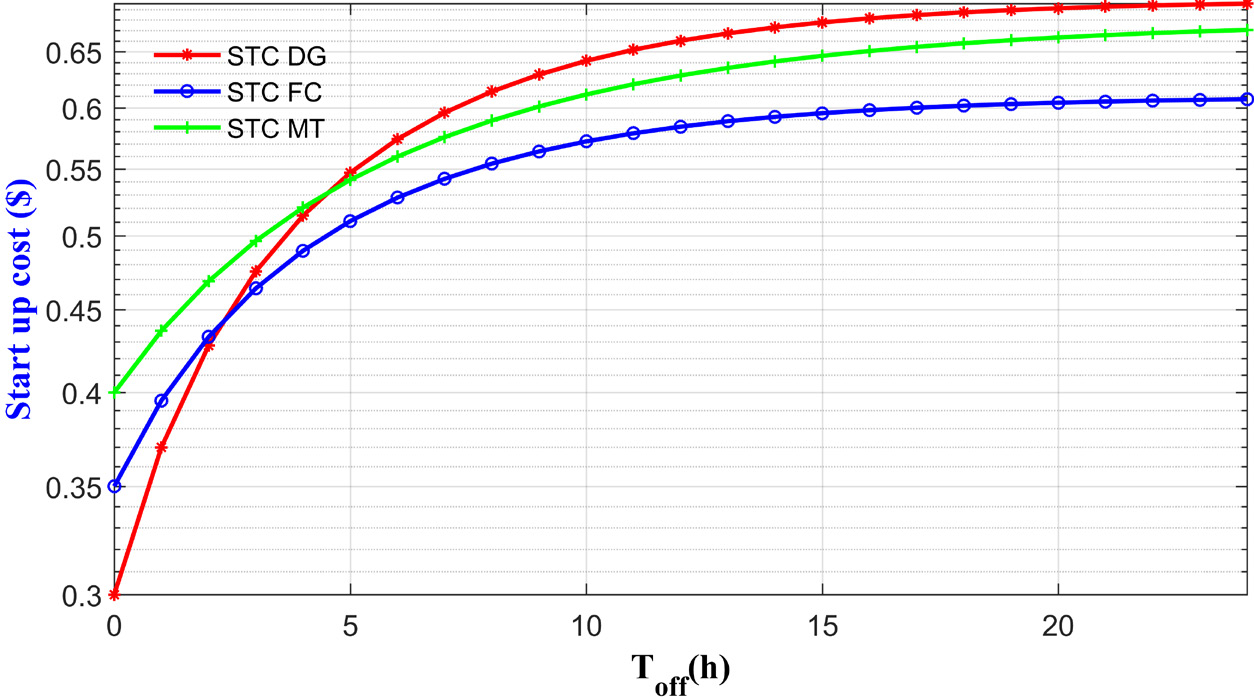
Depending on the time period that a CES has been off before its start-up. The start-up cost of each generating unit i is expressed as follows [22], [23], [33]. Figure 2 represents the start-up cost of DG, FC and MT, respectively:

$ST{C}_i={\sigma }_i+{\delta }_i\left[1-\text{exp}\left(-\frac{T_{\text{off},i}}{{\tau }_i}\right)\right]$ (11)

where σ_i and δ_i represent respectively, the hot and cold start-up cost of generating unit i in $/h. τ_i is the constant of unit cooling time of generating unit i. Finally, T_off,i refers to the unit shutdown duration in h.

Figure 2

Start-up cost of the dispatchable sources as a function of the time the unit has been off

• Exchanged power cost with the main grid

In the grid connected mode, the cost of exchanging power with the main grid can be mathematically expressed using the following equations [34], depending on whether the MG purchase or sell power from or to the connected main grid.

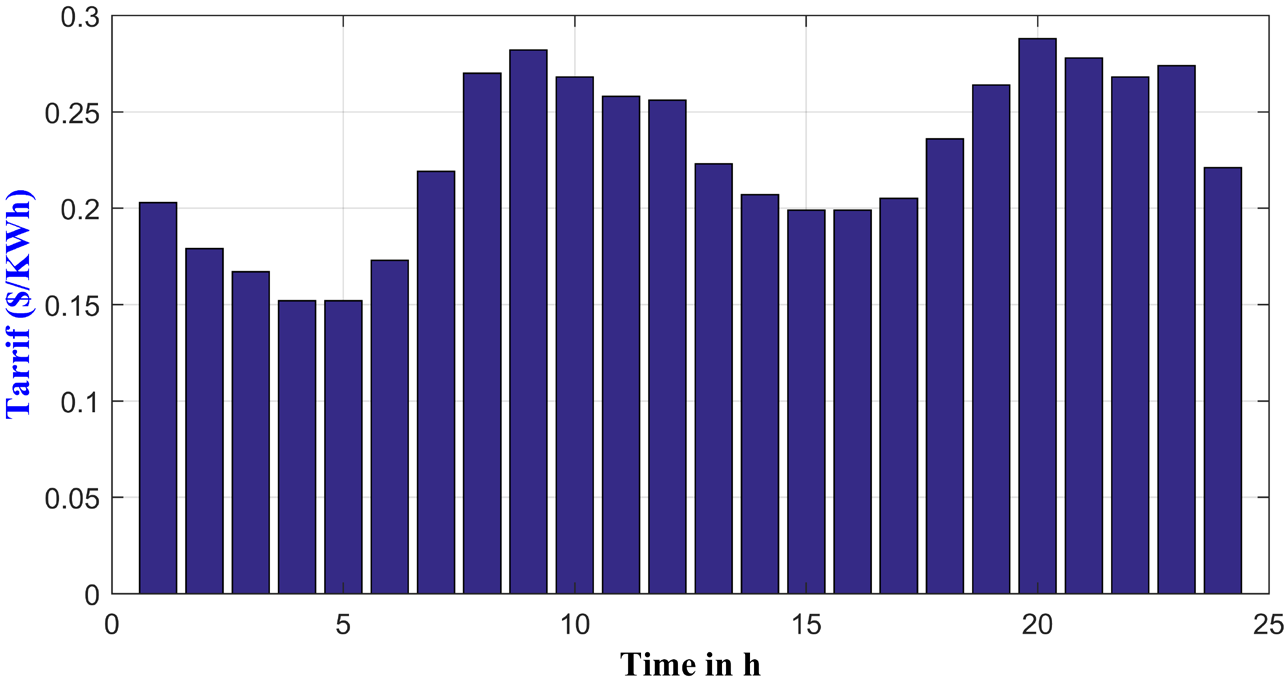
In this work, the day-ahead electricity price profile is chosen similar to the oneproposed in [35] as depicted in Figure 3:

$\begin{array}{l}CPE=C_{\text{p}}\times \text{max}(P_{\text{D}}-P_i,0)\\ RSE=C_{\text{s}}\times \text{max}(P_i-P_{\text{D}},0)\end{array}$ (12)

where, CPE and RSE represent respectively, the cost of purchasing and revenue of selling electricity to the main grid.

Pollutant gas emissions cost function.

The pollutant gas emissions cost of NO_x, SO₂ and CO₂, respectively, is defined as the second objective function to be minimized. It is expressed as a linear function of the produced power [32], [36]:

$F_2={\displaystyle \sum _{i=1}^N{\displaystyle \sum _{k=1}^M{\chi }_k(E{F}_{i,k}{P}_i)+{\displaystyle \sum _{k=1}^M{\chi }_k(E{F}_{\text{Grid},k}{P}_{\text{Grid}})}}}$ (13)

Table 1 shows the operating cost parameters and the emission rate coefficients of both CESs and the main grid used in this study. Moreover, the externality cost for NO_x, SO₂ and CO₂ emissions is set at 9.1714, 2.1617 and 0.0305 $/kg, respectively. As specified in [7], [22], [33]-[35]. Detailed input parameters of the studied MG components are given in Appendix 1.

Table 1

Operating cost and emission rate

	Prated	Fuel or gas cost coefficients				Start-up cost		O&M cost	Emission rate [kg/MWh]
			PBSSmin ≤
	Pi [kW]	αi [$/h]	PBSS(t) ≤	γi [$/kWh]	σi [$/h]	δi [$/h]	τi	KOMi [$/kWh]	NOx	SO2	CO2
			PBSSmax [$/kWh]
DG	40	2.22	0.2328	0.0024	0.3	0.4	5.2	0.01258	9.8883	0.2059	0.6495
FC	50	0.1037	0.1855	0.0009	0.35	0.26	5.2	0.00419	0.0136	0.0027	0.4889
MT	65	2.898	0.2668	—	0.4	0.28	7.1	0.00587	0.1995	0.0036	0.7239
Grid	50	—	—	—	—	—	—	—	1.6021	1.8016	0.8891

Figure 3

Day-ahead real time pricing signal

Power loss cost function.

The third term of the MOOD problem of eq. (6) represents the power loss cost of the conversion devices. Mathematically it is expressed as follows [16]:

$F_3={\displaystyle \sum _{i=1}^N{C}_{{\text{loss}}_i}{P}_{{\text{loss}}_i}={\displaystyle \sum _{i=1}^N{\sigma }_{{\text{loss}}_i}{C}_{{\text{loss}}_i}{P}_i}}$ (14)

In this study, it is assumed that the coefficient related to the power loss of converters is set at 2% for the FC unit, 4% when the power is generated from DG or MT unit. Finally, this coefficient is increased to 6% in case of exchanging power with the main grid.

Pareto dominance

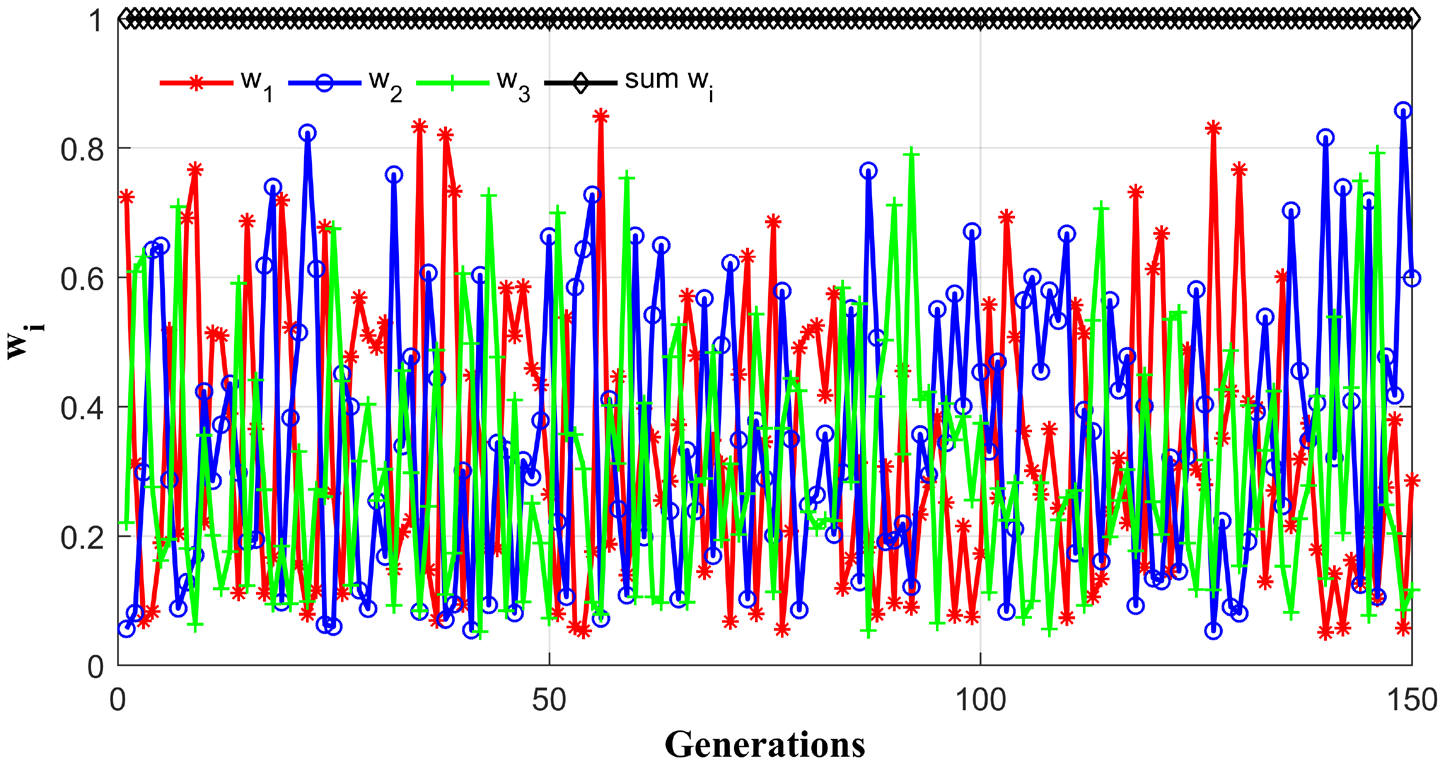
In the search space, a set of solutions called feasible solutions, can be obtained, according to different combinations of weight coefficients ω₁, ω₂ and ω₃ respectively. Figure 4 illustrated the various combinations of weight coefficients obtained for 150 generations.

Where for each generated combination, the following constraint should be taken into account:

${\omega }_i\ge 0\text{and}{\displaystyle {\int }_{i=1}^3{\omega }_i=1}$ (15)

Assumed that X₁ and X₂ are two solutions of the MOOP, X₁ is considered to dominate X₂ if and only if:

$\{\begin{array}{cc}{F}_i(X_1)\le F_i(X_2)& \forall i\in \{1,2,\dots N_{\text{O}}\}\\ F_i(X_1)\le F_i(X_2)& \exists i\in \{1,2,\dots N_{\text{O}}\}\end{array}$ (16)

In the search space, the non-dominated solutions are considered as Pareto solutions. The Pareto front consists of non-dominated solutions [37].

Figure 4

Different combinations of weight coefficients for 150 generations

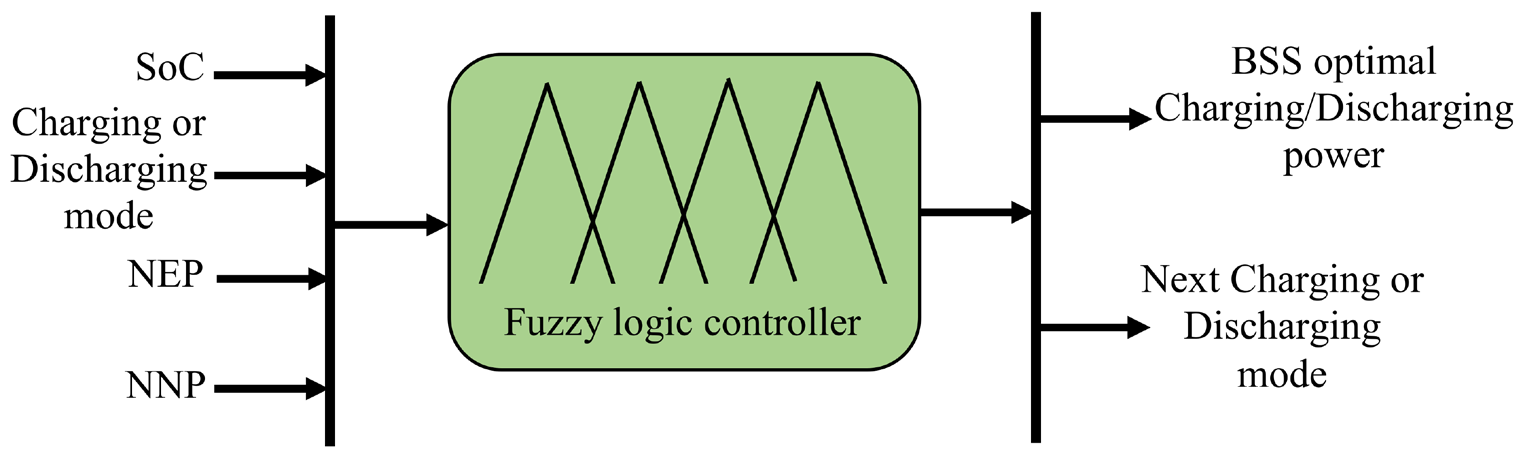
This work aims at developing a centralized control system for a day-ahead power management optimization and control of a typical MG system. The model is designed to operate in a two-level control architecture. The upper layer comprises two fuzzy logic control (FLC) subsystems. The first subsystem is implemented in order to define the participation of RESs, monitoring the battery SoC, the decision to start-up or shutdown the three CESs, load curtailment control in case of a grid failure, and the interactive mode between the main grid and the studied MG [39]. Whilst the second fuzzy logic controller is employed to ensure optimal scheduling of charging/discharging of the BSS [7], [40]. This FLC subsystem includes four inputs representing battery SoC, operating state of the battery (charging or discharging mode), normalized electricity prices (NEP) and normalized net power (NNP), that is defined as the difference between actual power demand and the available power from both RESs, and has two outputs representing the optimal charging/discharging power of BSS, and its next charging/discharging mode, respectively.

To describe the membership functions low, medium, high and very high, of the NEP's input respectively, the following abbreviations L, M, H and VH are used. The terms HC/D, MC/D and LC/D, in output membership function stand for high, medium and low charging or discharging of BSS. Finally, the abbreviations NE, ZO and PO, respectively correspond to negative, zero and positive normalized net power.

Figure 5 presents the structure of the fuzzy interference system for optimal charging/discharging of BSS. Finally, the detailed fuzzy scheduling rules for BSS are shown in Table 2.

The multi-objective optimization dispatch problem is solved using ALO algorithm, implemented in the bottom layer. Considering the minimizing of the operating cost, emissions level and power loss of conversion devices as objective functions. The obtained simulation results of the proposed ALO algorithm were compared with those provided from other heuristic optimization methods include PSO, ABC and WOA algorithm.

Figure 5

Structure of fuzzy logic control subsystem based optimal charging/discharging of BSS

In this section, to validate the effectiveness of the developed EMS, simulation is carried out for a day-ahead energy scheduling of a typical MG. Modelling and simulation of the optimization problem were conducted using MATLAB/Simulink environment, during 24 h and with a time step of ΔT=15 min. The aim of this study is the operation control and the optimization dispatch of the MG system in grid connected mode. Considering the minimizing simultaneously of the operating cost, emissions level and power loss of conversion devices. It is worth mentioning that the maximum supply capacity of DG, FC, and MT is set to 40 kW, 50 kW and 65 kW, respectively. The maximum imported power from the main grid is limited to 50 kW. Finally, the maximum charging and discharging power of BSS is fixed to 20 kW, while 10% and 80% are considered as the lower and upper limits on the SoC of the BSS. Finally, a comparison results with other well-known optimization algorithms include basic PSO, ABC and WOA approaches is detailed. The obtained simulation results are described hereafter.

Analysis of Pareto front

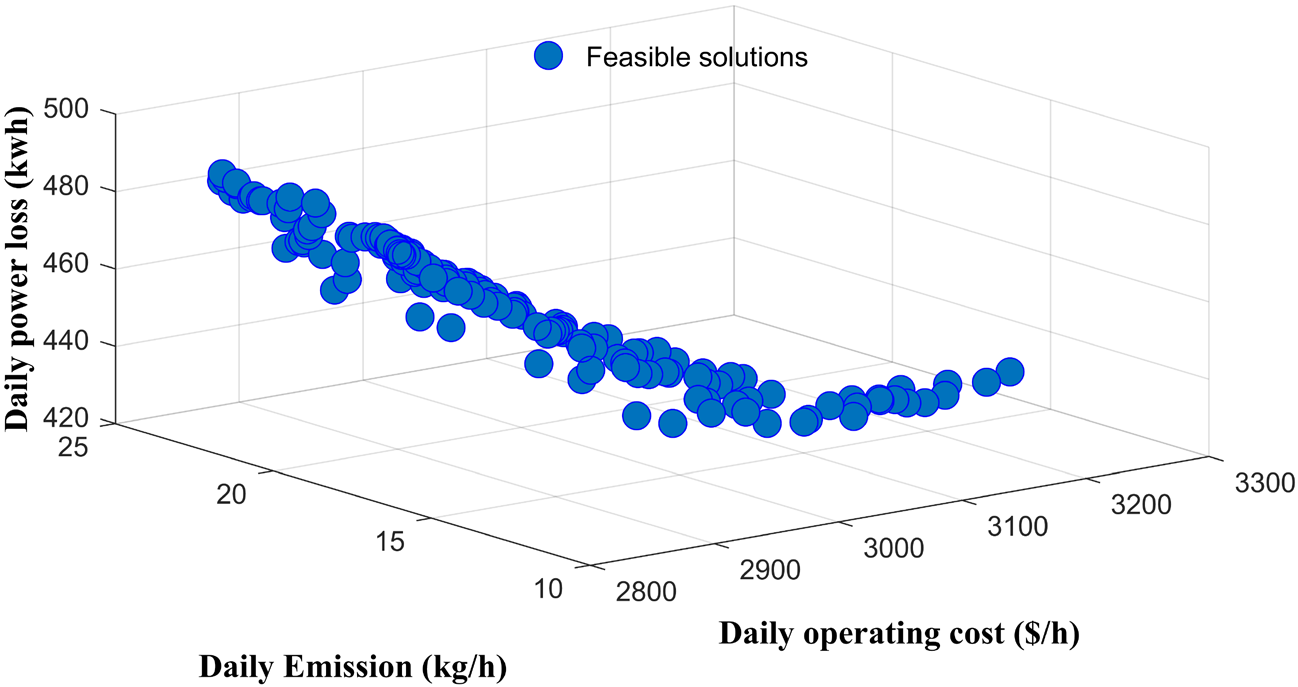
A set of solutions called feasible solutions can be produced by assigning various combinations of weight coefficients (ω₁, ω₂ and ω₃) to the formulated objective function as shown in Figure 6. Then, the formula provided in eq. (16) is applied in order to capture the Pareto optimal solutions only as illustrated in Figure 7. The results show that over 150 different combination of weight coefficients, only 57 combinations are kept to compose the Pareto optimal set. Finally, a fuzzy set approach is adopted for selection of the best compromise solution from the obtained Pareto optimal set.

Figure 6

Obtained feasible solutions under the proposed scheduling policy

Figure 7

Obtained non-dominated solutions under the proposed scheduling policy

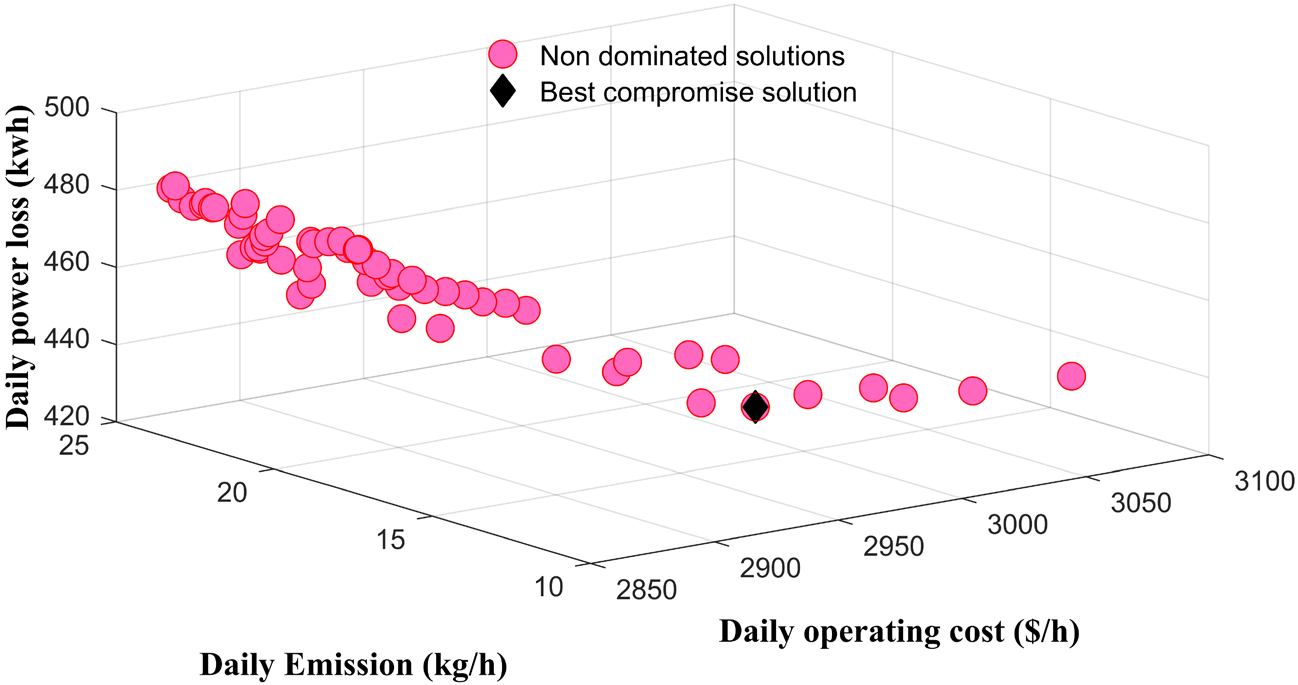
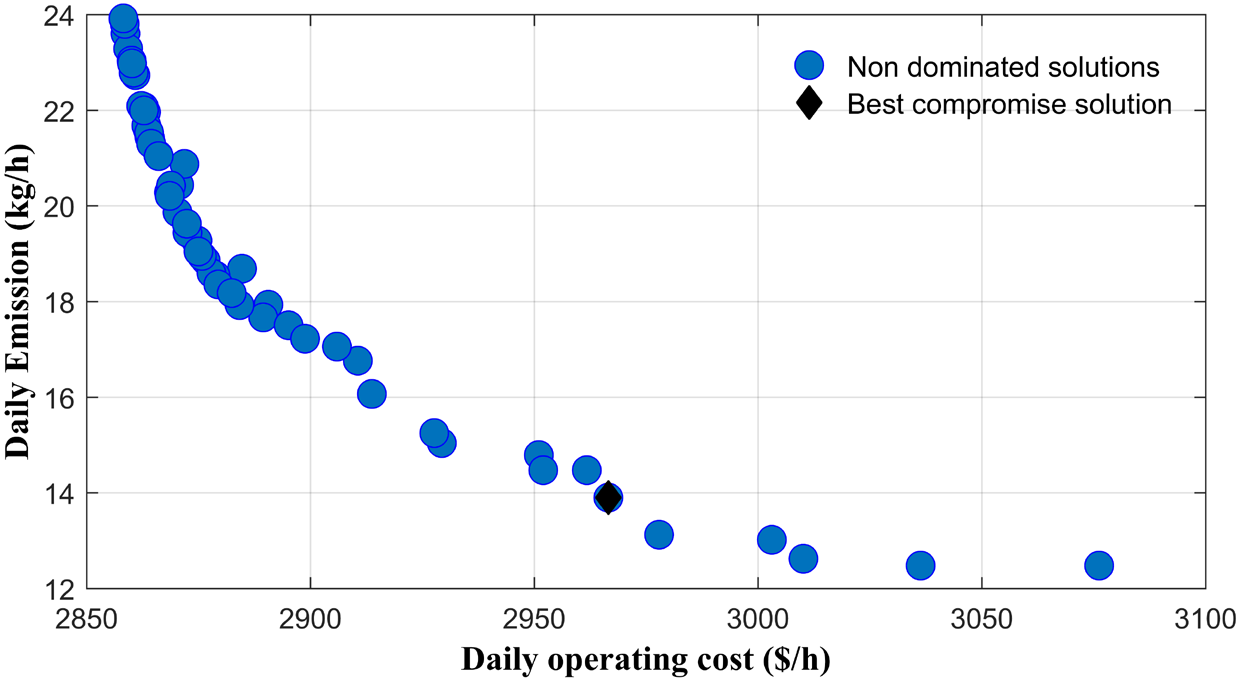
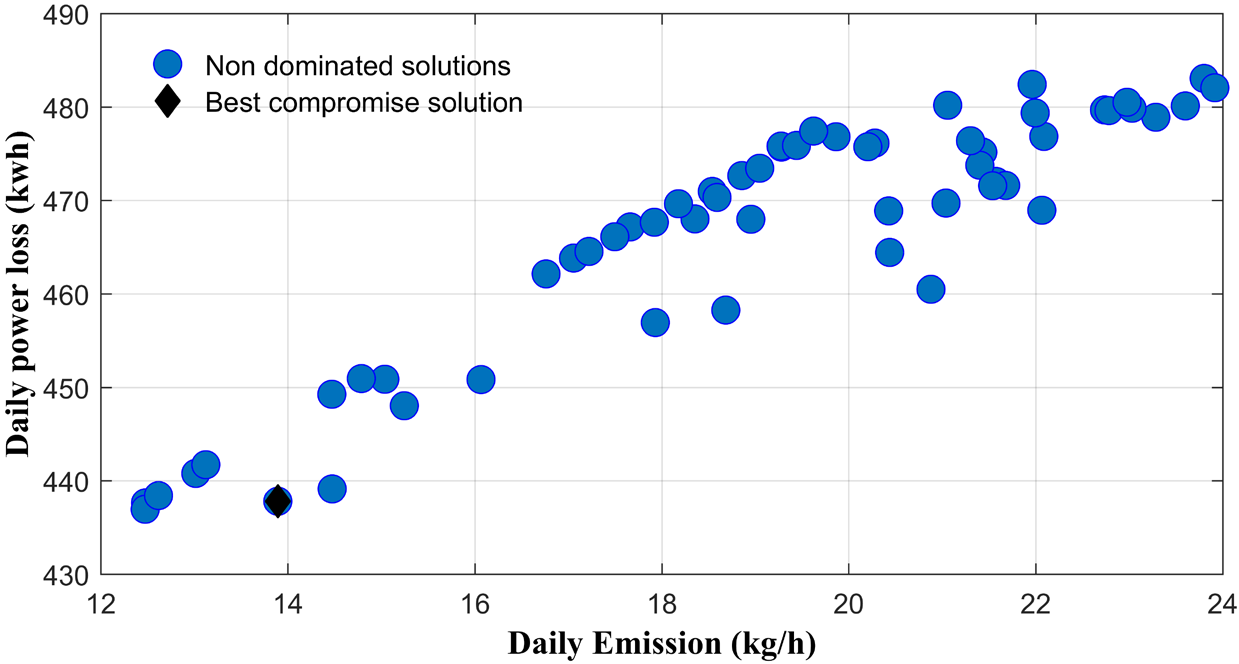
According to the results better compromise between the contradictory objective functions is achieved when ω₁ = 0.0892, ω₂ = 0.1209 and ω₃ = 0.7899 respectively. Figure 8, Figure 9 and Figure 10, respectively show the Pareto front obtained along with the compromise solution. Considering in each plot the evolution of two objectives simultaneously.

It is to be mentioned that the combination of weights related to the best compromise solution will be used in the following subsection for daily simulation of the MG operation.

Figure 8

Evolution of the emissions level as a function of the operating cost

Figure 9

Evolution of the power loss as a function of the operating cost

Figure 10

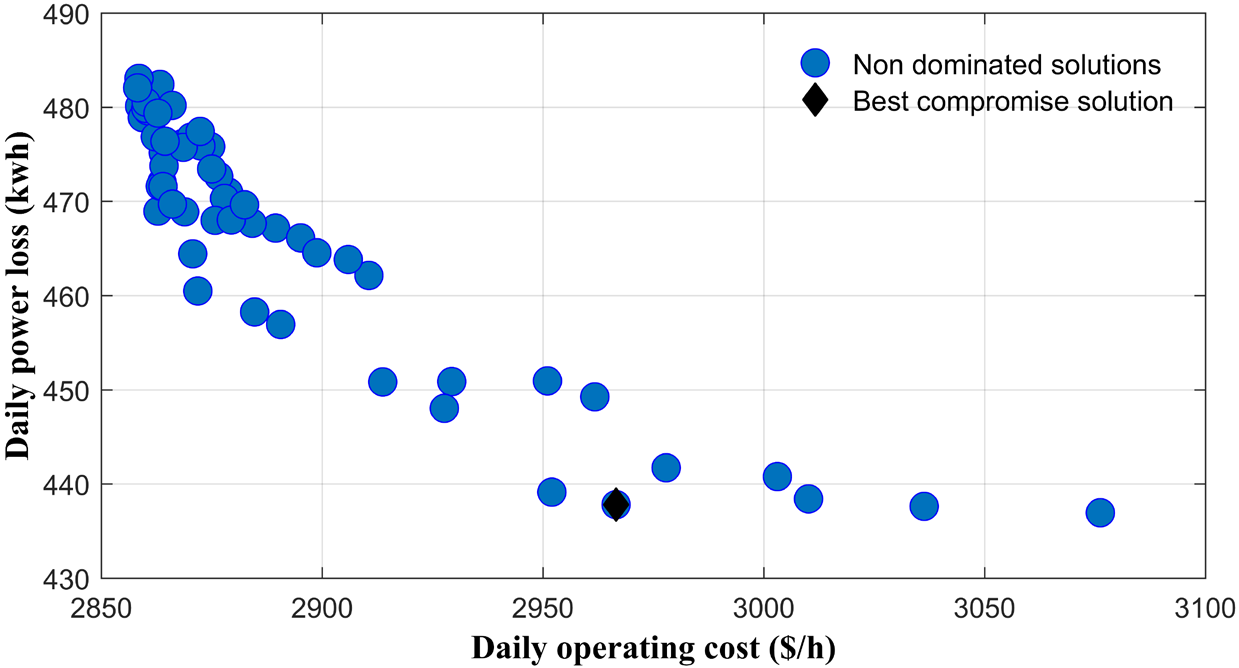
Evolution of the power loss as a function of the emissions level

Microgrid running under grid connected mode

The optimal sizing of the PV and WT unites is beyond the focus of this research work. Moreover, although the power generation of both PV and WT unites do not depend on fossil fuel, their price still higher than the other generation sources. This is due to their high capital cost [8]. In this study, the maximum PV and WT power values were 30 kW and 35 kW, respectively. Additionally, it is assumed that both RESs are equipped with a maximum power point tracking system, and they generate power without any emission of pollutants. The generation of both RESs, the optimal charging/discharging power of BSS, and the SoC evolution during the daily running simulation are shown in Figure 11. In this scenario, the battery is initially charged to 50% of SoC, and the load demand is primarily supplied by both RESs and the BSS during discharging mode.

Figure 11

Output power of RESs and optimal charging/discharging of BSS

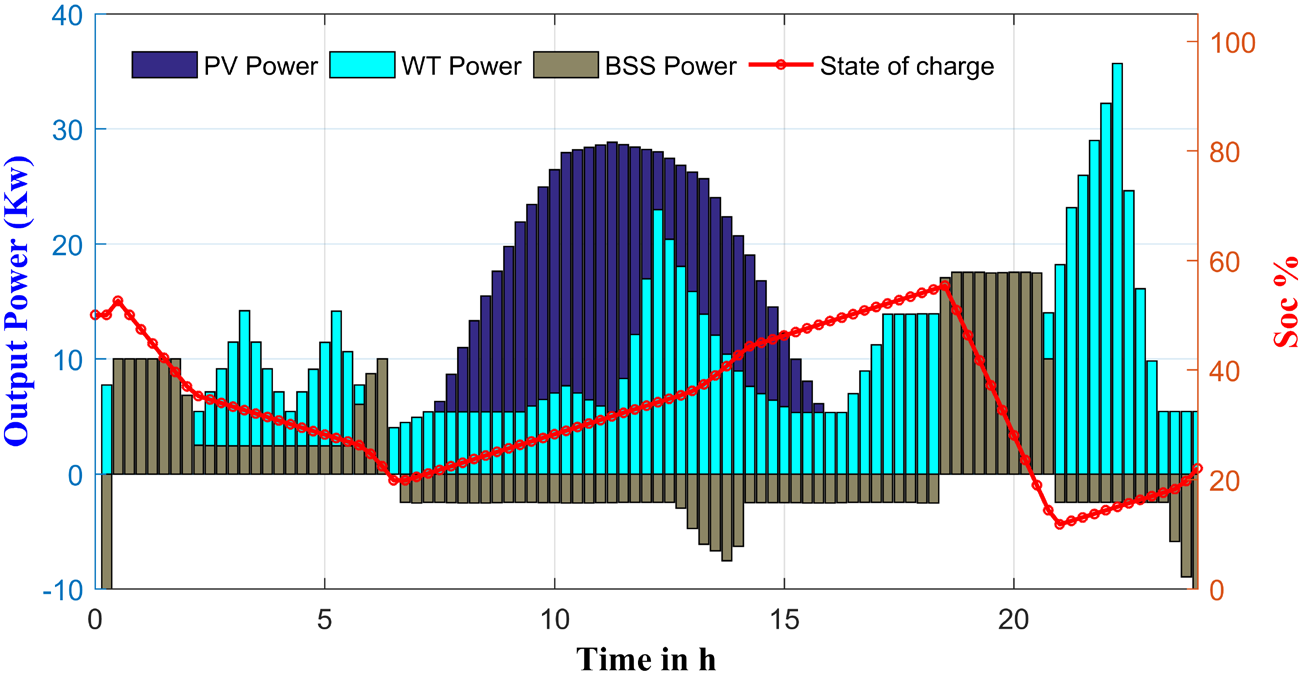
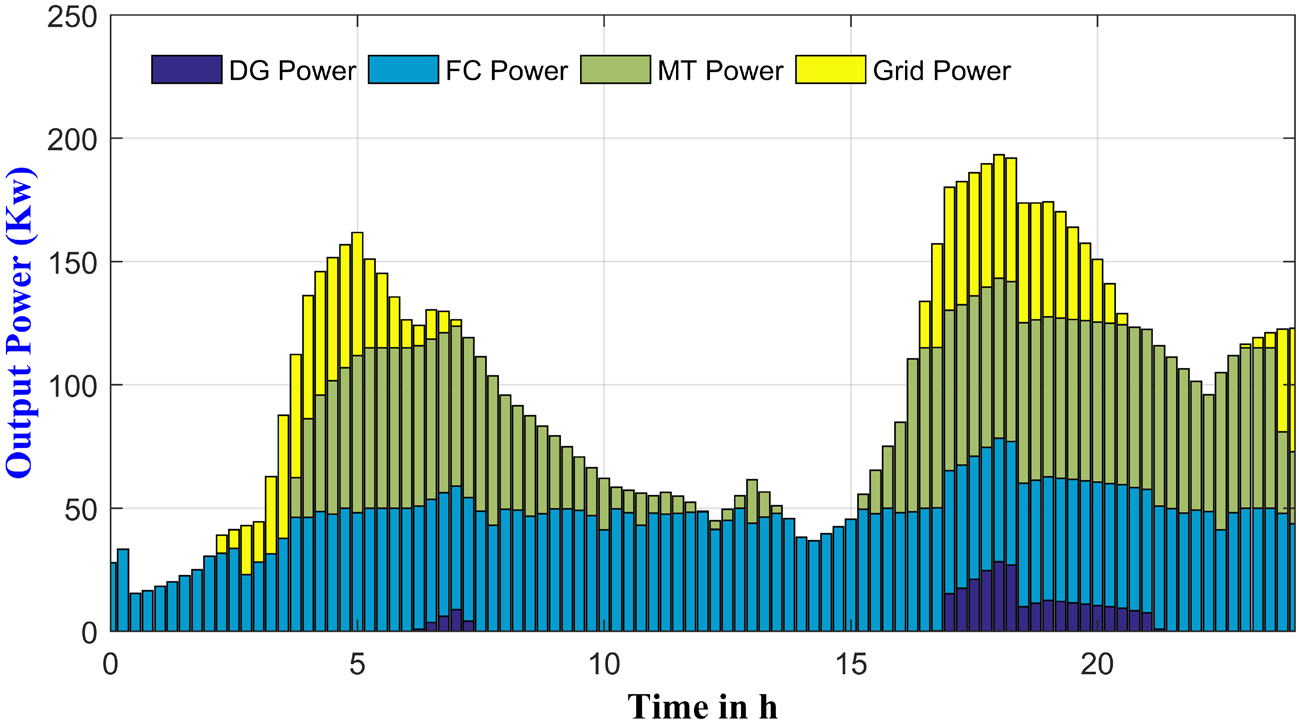
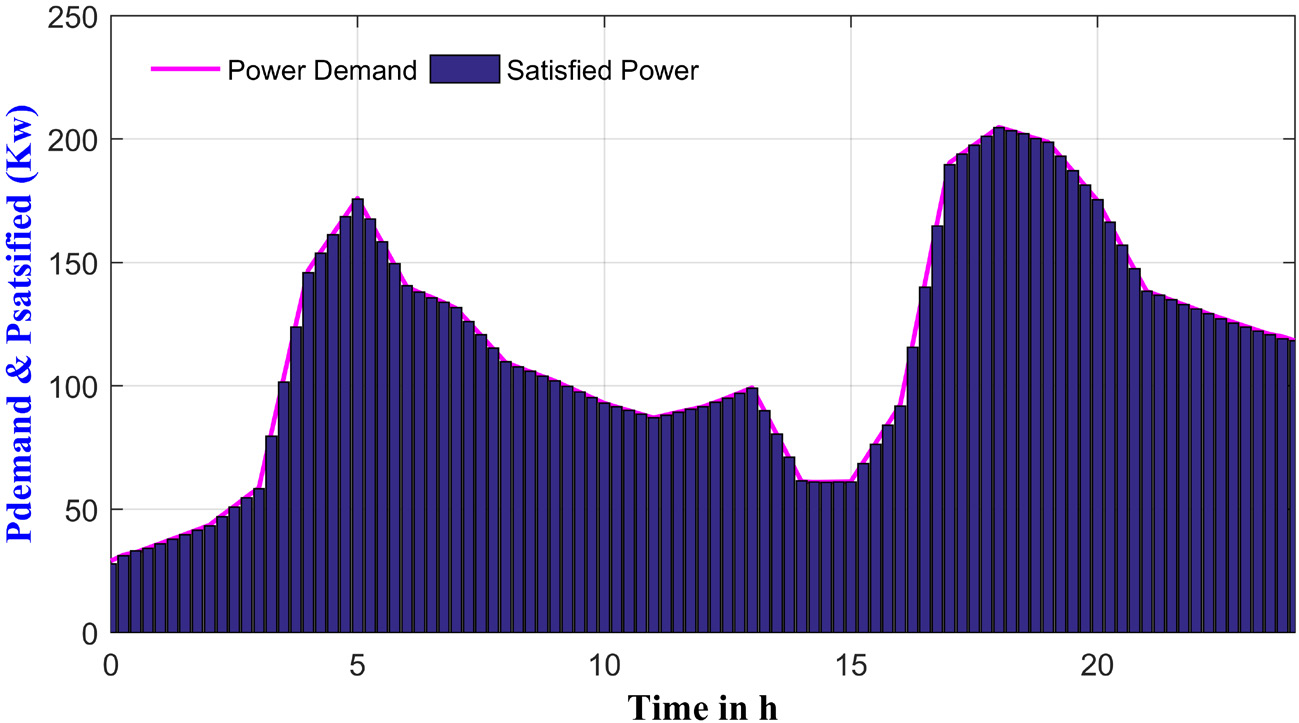
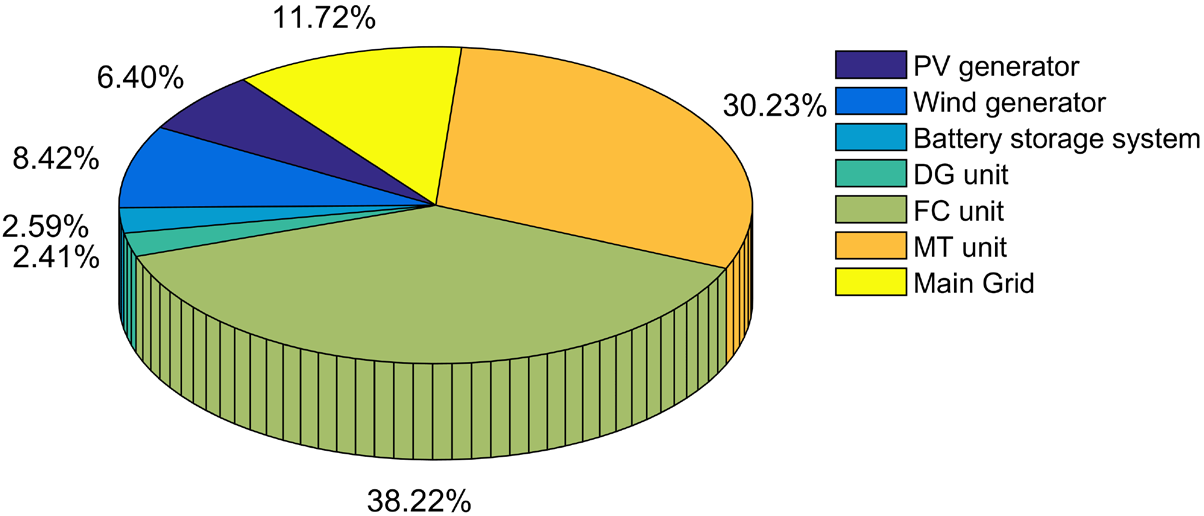
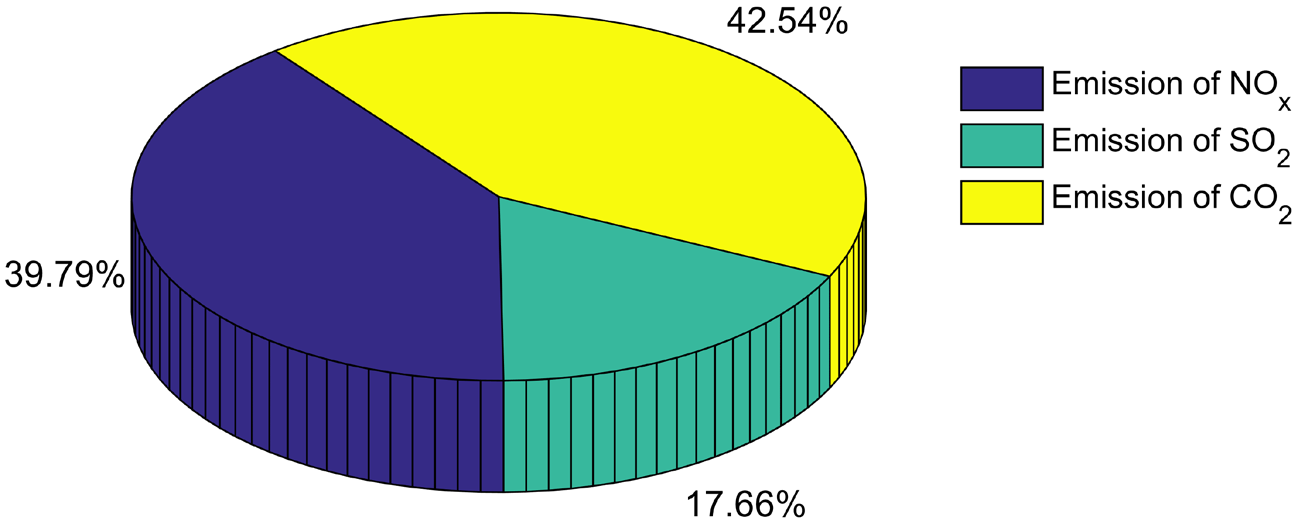
It can be observed that, the battery's SoCevolution is maintained within the pre-established range, avoiding the operation under extremes charge/discharge cycles. During the daily MG operation, the combination output power of the two RESs and the battery power supply during discharging cycles are not enough to fulfil the load demand. Therefore, the first FLC subsystem involves the three CESs in the energy management, while permit importing power from the main grid. Figure 12 shows the optimal output power of the three dispatchable sources represented by DG, FC and MT, as well as the imported power from the main grid, respectively. It can be seen that, under grid connected mode, a better compromise between the contradictory objective functions is achieved when the generated power from FC unit and MT unit, respectively is primarily used. The DG unit, though, was dispatched less time with fewer generation,only when the demand becomes higher, or at high-price periods when the main grid offers a high purchase electricity price, as it is the case from 20 h p.m. The considered load profile involves three kinds of demands, including residential load, commercial load and industrial load, with a total energy demand of 11.15 MWh. Figure 13 reveals the total system power balance between the required and satisfied power, it is obvious that no demand reduction is required, and the different power generation sources are able to cater the demand while considering the MOOD problem. The contribution rate of each power generation source in the studied MG is shown in Figure 14. It is clearly seen, that the total load demand is supplied by 38.22% FC unit, 30.23% MT generator. Contrary, the contribution rate of the DG is limited to 2.41%, as it has the highest operating cost and pollutant emission level. In addition, Figure 15 represents the emissions level of NO_x, SO₂ and CO₂, respectively for a daily simulation time. It can be seen that an almost 42.54% of these emissions are caused by CO₂ pollutant, followed by the emission of NO_x. Whereas the emission of SO₂ is limited to 17.66% of the total daily emissions. Table 3 summarized the obtained simulation results, compared with the previously published work [40], based on the analytic hierarchy process (AHP) [41] technique for weight determination, and according to a priory preference of the objective functions. It is clear that, from an economic point of view, importing power from the main grid is more beneficial, it provides a cost saving of 33.47%, however the emissions level and the power loss of conversion devices related to the obtained weights using AHP method become higher, with an increase of 29.87% for emissions level and 8.54%, for the power loss. Moreover, by comparing the power imported from the main grid using both approaches, it is obvious that the proposed approach allows a maximum generation from the internal MG's sources and less energy dependence from the main grid. Which is desirable, especially in case of unexpected grid failure.

Therefore, if no prior preference is required, the fuzzy set seems to be an effective tool to find the best compromise solution.

Figure 12

Optimal power generation of CESs and the main grid

Figure 13

Microgrid system power balance

Figure 14

Contribution of each generation source in power management

It is worth mentioning that, in order to confirm the validity and effectiveness of the proposed methodology to deal with the MOOD problem in a DC microgrid, the simulations are performed for a typical daily load profile, varying between about 60.8 kW and 204.7 kW. However, there is no reason why the studied MG power system cannot be extended, either by including new generating units or by changing the daily load profile or the capacity of the installed generation sources.

In summary, it appears that the developed energy management system is flexible, scalable and easy to adapt to future needs, depending on the user's requirements.

Figure 15

Emission type level under the proposed scheduling policy

Table 3

Simulation results obtained for a daily microgrid operation under grid connected mode

Output Variables	Using fuzzy set forweights determination	Using AHP for weights determination	Data Percentile (%)
Daily Fitness Cost [$/day]	350.0163	1860.1402	—
Daily Operating Cost [$/day]	2964.2615	1972.1086	+33.4705%
Daily Emission levels [kg/day]	13.9830	19.9384	−29.8690%
Daily Power Loss of conversion [kWh]	438.3214	479.2676	−8.5435%
Daily Power Generated by RESs [kWh]	1677.8502	1677.8502	0.0000%
Daily Power Generated by CESs [kWh]	8021.2663	6074.9071	+24.2650%
Daily Exchanged Power with the grid [kWh]	1326.4354	3272.7946	−59.4709%
Daily Emission level of NOx [kg/day]	5.5641	7.4902	−25.7149%
Daily Emission level of SO2 [kg/day]	2.4699	5.9499	−58.4884%
Daily Emission level of CO2 [kg/day]	5.9490	6.4983	−8.4530%

Comparison results

This section is dedicated to comparing the results achieved using ALO algorithm and the other heuristic methods to solve the MOOD problem. The number of population size and the maximum number of iterations are set to N_p = 40, and 100, respectively.

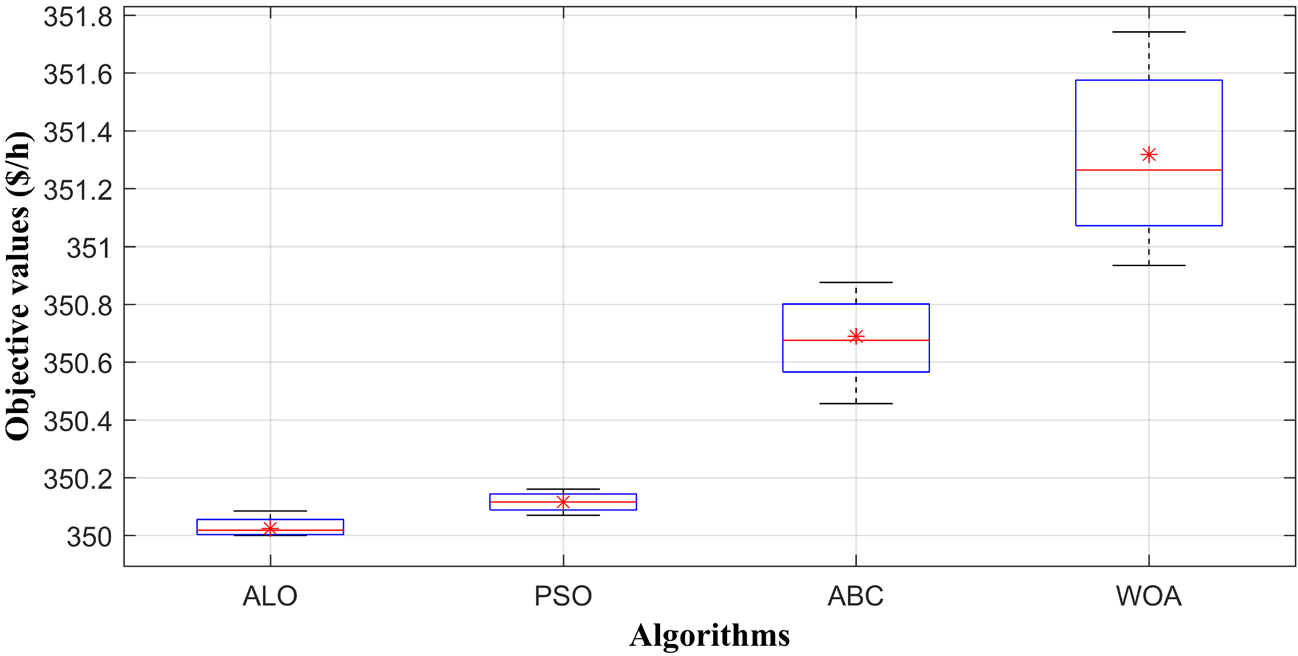
Table 4 and Figure 16 show the performance comparison based on daily MG operation, calculated for 30 trial runs. It is clear that the proposed ALO approach is more costeffective, it has the strong ability to avoid premature convergence and find optimal solutions compared to the other proposed algorithms. From the obtained best cost, worst cost, mean cost, median cost and standard deviation values, that the proposed method has the best performance and provides better robustness and stability. Therefore, the obtained results indicate the outperformance of ALO algorithm over the PSO, ABC and WOA heuristic techniques.

Table 4

Daily comparison of algorithms for 30 runs

Algorithms	Best cost [$/h]	Worst cost [$/h]	Mean cost [$/h]	Median cost [$/h]	Standard deviation [$/h]	Computational time [s]
ALO	349.999965	350.084612	350.024766	350.018311	0.020574	1458.417102
PSO	350.069594	350.160135	350.116406	350.115911	0.022118	2337.050108
ABC	350.456024	350.875535	350.689149	350.675215	0.086947	1501.167555
WOA	350.934205	351.742203	351.318476	351.264350	0.200734	281.838117

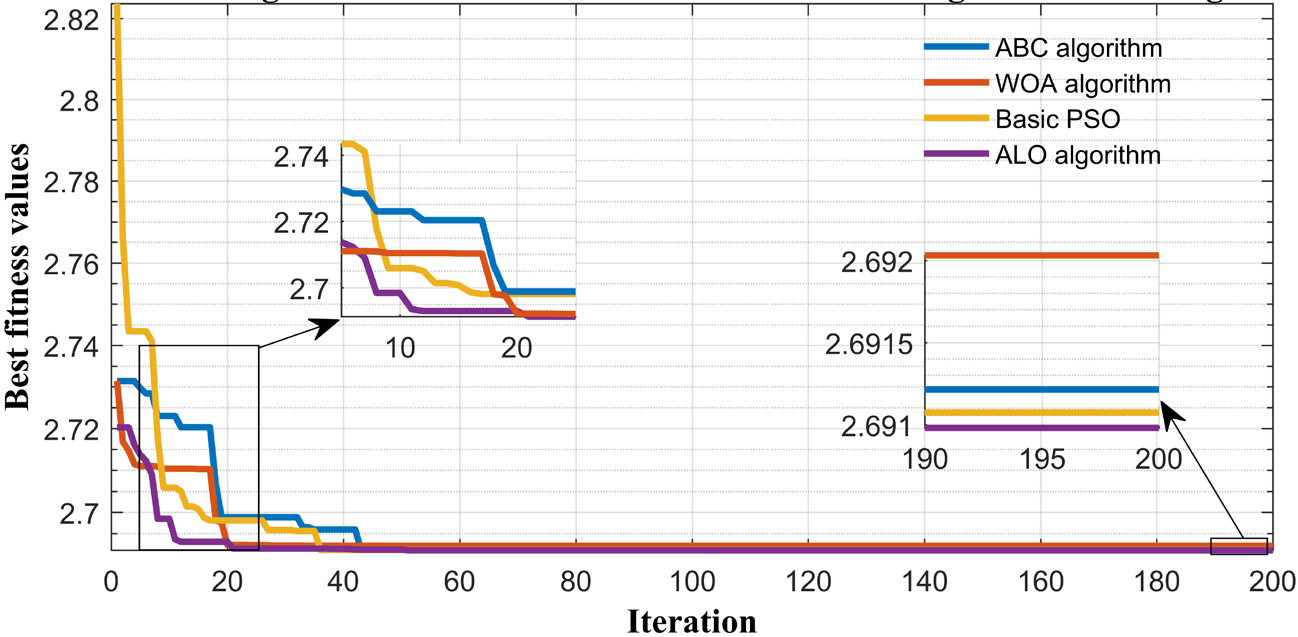
The comparison of the performance of ALO algorithm with other heuristic techniques in terms of the convergence characteristics based on a fixed load demand and a maximum number of iterations of 200 is illustrated in Figure 17. Compared to the other algorithms, it is shown that, the ALO approach converges better to the global optimal solution. Also the proposed algorithm provides good performance in terms of convergence speed and time, since it requires less time and fewer iterations to converge to the global optimal solution. Also by comparing the computational time for a daily simulation of MG operation, it can be concluded that ALO method is computationally efficient, since it provides the second best computational time.

In summary, the ALO algorithm seems to become a promising solution for dealing with complex optimization problems in modern power system due to its superior performance in terms of stability, good convergence and computational time.

Figure 16

Comparison of algorithms using box plot for 30 trial runs

Figure 17

Comparison of the convergence of the algorithms based on a fixed load demand

In this study, a new EMS for operation control and optimization dispatch of a grid connected MG is proposed. Considering the minimizing simultaneously of the operating cost, emissions level and power loss of conversion devices.

The proposed EMS is designed to operate in two layers' architecture, combining two fuzzy logic subsystems in the highest level, implemented in order to optimize scheduling of battery's charging/discharging cycles, monitoring the SoC of the BSS and the interactive mode between the main grid and the studied MG. While the bottom hierarchy level of the proposed EMS contains an ALO algorithm dedicated to solve the multi-objective optimization dispatch problem.

The effectiveness of the proposed ALO method to deal with the formulated MOOD is validated by comparing the results of those provided by PSO, ABC, and WOA heuristic techniques. The obtained simulation results demonstrate the outperformance of ALO in terms of the convergence speed, stability, and computational time. It can be summarized that the proposed methodology guarantees a real time operation control and optimization dispatch of MG, considering technical, economic and environmental tasks simultaneously.