Decentralization of the energy systems is observed in different countries [1]. Although one can observe a substantial diffusion of distributed photovoltaics (PV) among households in the last years, different diffusion levels are seen depending on the country [2]. In particular, it is visible when one compares developed and developing nations worldwide. Developing nations present a still incipient diffusion in the household sector, as observed in India, Brazil, and Mexico.

In India, the installed capacity of power plants comprises 63.6% capacity from fossil fuels, 2% from nuclear, 13% from hydro, and 21.4% from renewable energy sources [3]. Carbon lock-in hinders the penetration of solar energy in the system due to the dominance of fossil fuels. Solar contributes 7% to the installed capacity. The Jawaharlal Nehru National Solar Mission aims to achieve 100 GW of solar by 2022 [4]. The installed solar capacity is 26 GW by January 2019, and the solar rooftop PV installation is 3.399 GW as of September 2018 [5]. With a compound annual growth rate of 88% [5] in the last five years, the growth rate is still lower than the required trajectory for achieving the government target of 40 GW by 2022 for rooftop installations. The CAPEX-based business models or PV diffusion in India are still the major contributors to the development of rooftop PV in India, as other models are still not so successful in promoting the growth of the technology. However, OPEX-based installation of rooftop PV has increased to 35% of capacity addition in 2018 [5], which shows that such a market is extremely dynamic and changing rapidly. The initiatives of the government of India are usually towards the reduction in upfront costs of PV through subsidies, lower interest on debt, tax incentives, and tariff benefits.

Figure 1 shows the contribution of the main sectors of the economy toward the installed capacity of rooftop PV in India [5].

Figure 1

Rooftop PV installation based on customer segment in India

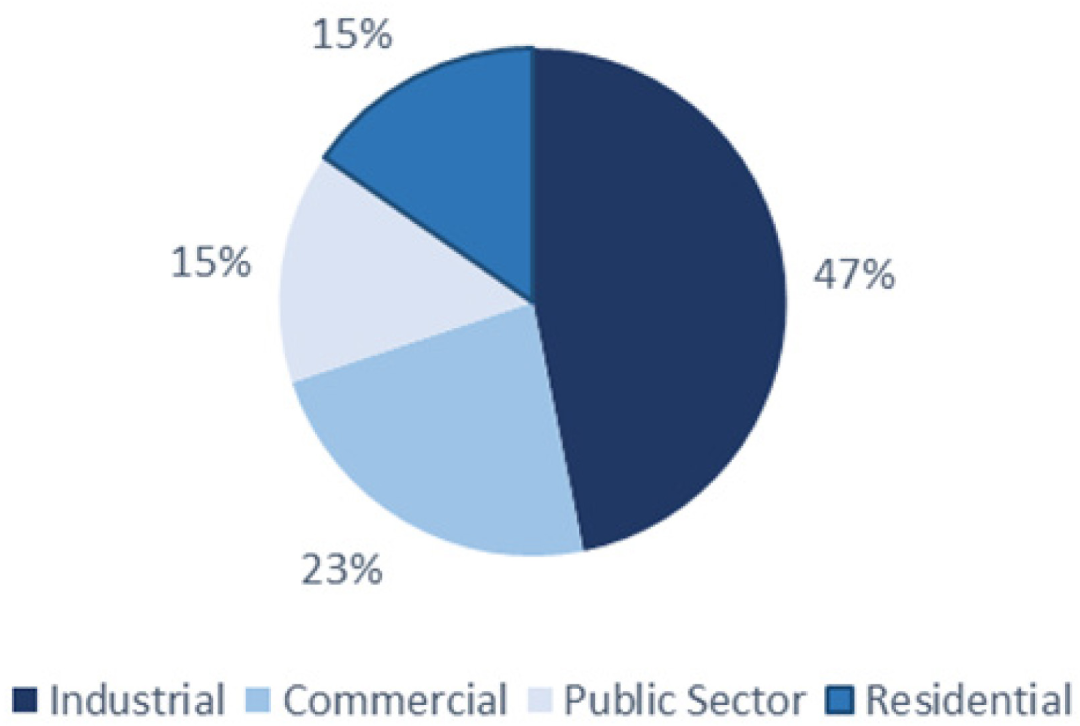
The contribution from the commercial and industrial consumers is high as they pay higher tariffs for electricity and increased subsidies for rooftop PV adds to their savings on electricity. The residential sector comprises 15% of all the sectors, and the favorable policies from the government like net metering policy and newer business models, which aid in upfront costs, would play a pivotal role in the future growth of residential rooftop PV. A direct impact of a higher percentage in this market would be to help the country achieve renewable energy goals of emission reductions.

India has 250-300 solar days with solar radiation of 4-7 kWh/(m² day) [4]. With this abundant solar resource, the diffusion of PV in India would increase energy access through green energy production and energy security and would help to connect rural areas. Although a substantial increase in electricity access has been observed in the last decade in rural areas, there are still many households without this access [6]. And when PV is used for electrification, battery issues might be an important point to consider [7].

The diffusion of new technologies usually follows an S curve, which has been used to study the expansion of different processes like adopting air conditioners, consumer goods, etc. [8]. The main idea of models to investigate the diffusion characteristics is to capture the slow increase in the market at the beginning, a faster intermediate phase, and a deacceleration at the end when the product or the technology has almost reached the final potential market. These models are the Cumulative Lognormal, Cumulative Normal, Gompertz, Log Reciprocal, Logistic, Modified Exponential, Weibull, and the Bass model [9]. The study of the diffusion of renewable technologies is important for developing strategies to meet climate and sustainable development goals. Diffusion modelling is an essential tool for assessing policies and aids policymakers in revising market mechanisms to achieve the requisite pace for the growth of renewable energy technologies.

Many studies analyse the diffusion modelling for PV growth in different countries. One of the most well-known models in the literature for tackling the diffusion of PV systems is the Bass model. The theoretical foundation of the Bass model is one of the major elements for preferring it to other possible S-shaped models since it identifies consumer adoption as the main driver of diffusion [10]. Model parameters represent the role of innovators and imitators in technology diffusion. This model was used to analyse the PV adoption level in several countries [10]. In California, it was found that the coefficient of imitation and the level of education are inversely related, and the price-based fluctuations impact the adoption rates [11]. In an analysis of the diffusion of PV in Germany, a system dynamics model was used to study the impact of feed-in tariffs on PV adoption. It was observed that the policymakers should make decisions on feed-in tariffs as soon as possible to maintain trust in the consumers for the continued promotion of the technology. There has been significant growth in the demand for PV in Germany in the last decade, leading to a decrease in prices. The market for small-scale PV is almost saturated, and a mix of Renewable Energy Targets would help achieve the renewable energy goals. In addition, public policy plays a significant role in the transition toward a greener economy [12].

Another study analysed the household-level innovation diffusion model for Ontario, Canada using discrete choice experiments to predict the probabilities of PV adoption time. The study showed that awareness among consumers about technology and savings achieved have a critical impact on the adoption rate and emphasised the importance of effective education [13]. In a study conducted for households in Italy, an agent-based model was used to study the diffusion of PV. The results indicated that the feed-in tariff scheme had boosted PV adoption that would continue at a slower pace. The stepwise reduction in financial incentives would lead to stable PV diffusion compared to a steep reduction in incentives, which would drop the diffusion process significantly [14]. Studies were also conducted in the Netherlands regarding adoption factors [15], and discussions about feed-in tariffs for solar were carried out in Japan [16] and Germany [17].

In India, a forecast of electricity generation using a nonlinear Bass diffusion model indicates that the growth of fossil-fuel-based resources will be dominant; however, renewables will contribute to 22% of the generation mix by 2030 [18]. Since distributed PV diffusion in the residential sector is still in the initial stages in India, applying the Bass model to forecast diffusion in the PV market can be tricky. It is difficult to choose the parameters since insufficient historical data are available to fit the Bass model curve and estimate parameter values.

Some work has been conducted in developing markets, such as Brazil, with a borrowing approach from the solar water heater (SWH) market [19], which is a much more diffused technology and presents more consistent values for the model parameters. However, PV in that market is used more as a replacement for existing sources of already connected communities [20]. To the best of the authors’ knowledge, no papers in the literature show how this “borrowing approach” applies to markets where PV is also used to provide the first source of electricity to local communities. This paper uses the said approach to analyse PV diffusion in a residential market with such characteristics. India is used as a case study, projecting values for future diffusion in this market.

This paper is organised as follows: Section 2 presents the methods used for calculating the final potential market and Bass model parameters of the SWH market, and section 3 presents the results of borrowing the parameters from one market to another and a brief discussion of such results. In section 4, a conclusion with the main findings and potential suggestions for future work is presented.

Using the system dynamics approach, a Bass diffusion model is analysed for studying the rooftop PV adoption rate in a market with PV that is used as a source of primary electricity for local communities. In the first step, the data are collected for the historical installed capacity of rooftop PV and solar water heaters in India. The data sources are reports from the Ministry of New and Renewable Energy (MNRE) [4] and reports from Bridge to India, a consulting company in the renewable energy market in India [5]. Then, the final potential markets of SWH and PV are estimated based on the total number of households in India. In the sequel, the Bass model parameters are estimated for the SWH market based on the diffusion of SWH in India and used as proxies for the incipient rooftop PV market. Finally, a comparison is drawn between the projected diffusion of rooftop PV based on SWH parameters and diffusion of PV based on Bass model parameters from a more consolidated household PV market, such as the USA.

As residential rooftop PV diffusion in India is still incipient, a robust dataset is not available from which parameters to model the adoption of distributed PV technology can be derived up to its final diffusion. Hence, SWH historical data are used to obtain the Bass model parameters, based on a similar approach in the literature [19]. This approach is justified because the SWH market carries several similarities with the rooftop PV market. Both technologies are mostly rooftop-mounted and use the solar resource as input. Moreover, they are being mainly developed under similar business models since financial returns are obtained from electricity bill savings across subsequent months. Demographic similarities between both markets should also be pointed out since both markets are composed of individual and distributed house owners who can install a system on their rooftops based solely on individual decisions.

Final potential market

The final potential market is the total potential capacity that could be installed on rooftops for PV and SWH in India. It is calculated by an external estimation method based on the country’s demographic, technological, and economic features [19]. Developing estimates by fitting historical data in an S-curve is not recommended as this could lead to significant underestimations [21], [22].

Figure 2

Layers used for the final potential market estimation

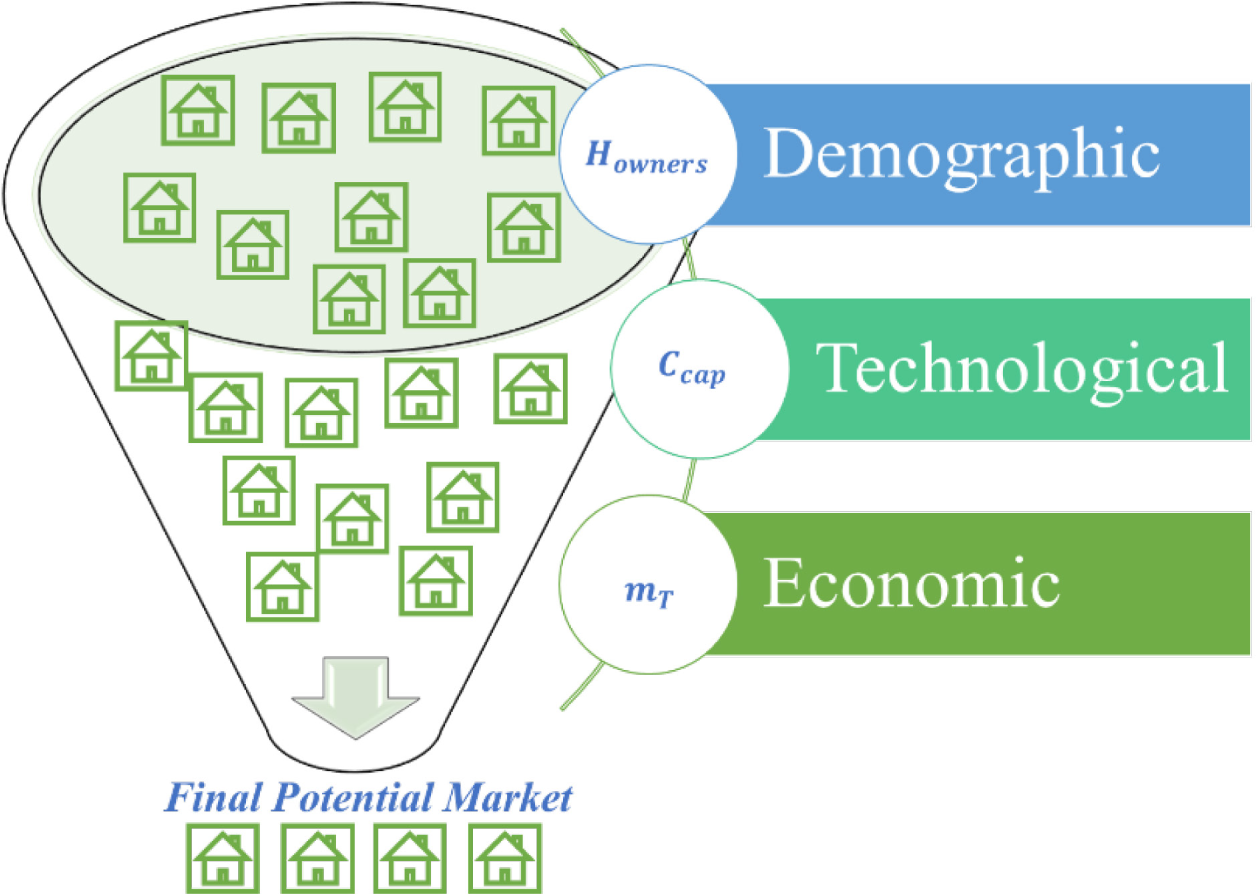
The data for filtering each layer are collected from the Indian government websites for the number of households and percentage of rural and urban households [23], [24]. As explained in each topic below, data from the literature [25] and [26] are also considered.

The potential markets at t = 0 and t = T are estimated considering the following procedure in the demographic, technological, and economic layers, as represented in Figure 2. The final potential market is estimated based on demographic, technological, and economic considerations.

Demographic layer

(D1) Retrieve the total number of households in India, $H_{\mathrm{total}}$. This number is obtained from the Indian Government Statistics based on [23] and [24]. (D2) Estimate the total number of houses owned by the household, $H_{\mathrm{owners}}$, since rental households cannot decide to install the technology by themselves:

$H_{\mathrm{owners}}=H_{\mathrm{total}}\times f_{\mathrm{owners}}$ (1)

where $f_{\mathrm{owners}}$ denotes the share of total households owned by the people residing in the households.

Technological layer

(T1) Estimate the total number of available households $H_{\mathrm{cap}}$, excluding those with shadow, tanks, antennas, and a cross-competition between SWH and PV for the same space. This capability factor is given by $f_{\mathrm{cap}}=0.85$ for PV, according to [25] and f_cap = 0.75 for SWH, due to additional necessary modifications in the plumbing systems for SWH technology:

$H_{\mathrm{cap}}=H_{\mathrm{owners}}\times f_{\mathrm{cap}}$ (2)

(T2) Estimate the total capacity ($C_{\mathrm{cap}}$) of installed power for PV and area for SWH, considering that rooftops will have an average SWH size of $\overline{c}=2{\text{m}}^2$ and average solar panel size of $\overline{c}=3\text{kWp}$ [25]:

$C_{cap}=H_{\mathrm{cap}}\times \overline{c}$ (3)

Economic layer: (E1) Estimate the maximum market share $mm{s}_0$ at t = 0:

$mm{s}_0=e^{-f\times P{B}_0}$ (4)

where f denotes sensibility factor, estimated at 0.3 by [26] for the PV market, and $P{B}_0$ is the payback time in years. Final payback time of 3 years for PV and 1 year for SWH for the final diffusion period of the analysis have been considered.

(E2) Calculate the initial potential market $m_0$ by multiplying the estimated total capacity with the fraction $mm{s}_0$ obtained in the previous step:

$m_0=C_{cap}\times mm{s}_0$ (5)

(E3) Calculate $m_T$ according to eq. (6), taking the value of $t=T$ as a long-term period for diffusion. The final potential market after T years with a yearly household increase (at a rate of 0.02 assumed here), using the accumulated rate denoted $rate\_po{p}_T$ is:

$m_T=m_0\times rat{e}_{-}po{p}_T$ (6)

The approach presented above is applied in the Indian market. This section includes a case study and discussion of the diffusion results in the said market.

Case study

India was chosen to represent an application of this approach based on this paper’s hypothesis. Table 1 presents SWH diffusion parameters for India obtained by a nonlinear curve fitting with historical data and summarises the statistical t-test results.

Table 1

Parameters for the SWH market in India based on the historical annual data

Parameter	p	q	$m_T$* [106m2]
Value	0.00105	0.12219	205.46
T-test results**	p-value = 0.93645		h = 0

*

estimated final potential market;

**

h = 0 does not reject the null hypothesis at the 5% significance level that residuals have zero mean and unknown variance

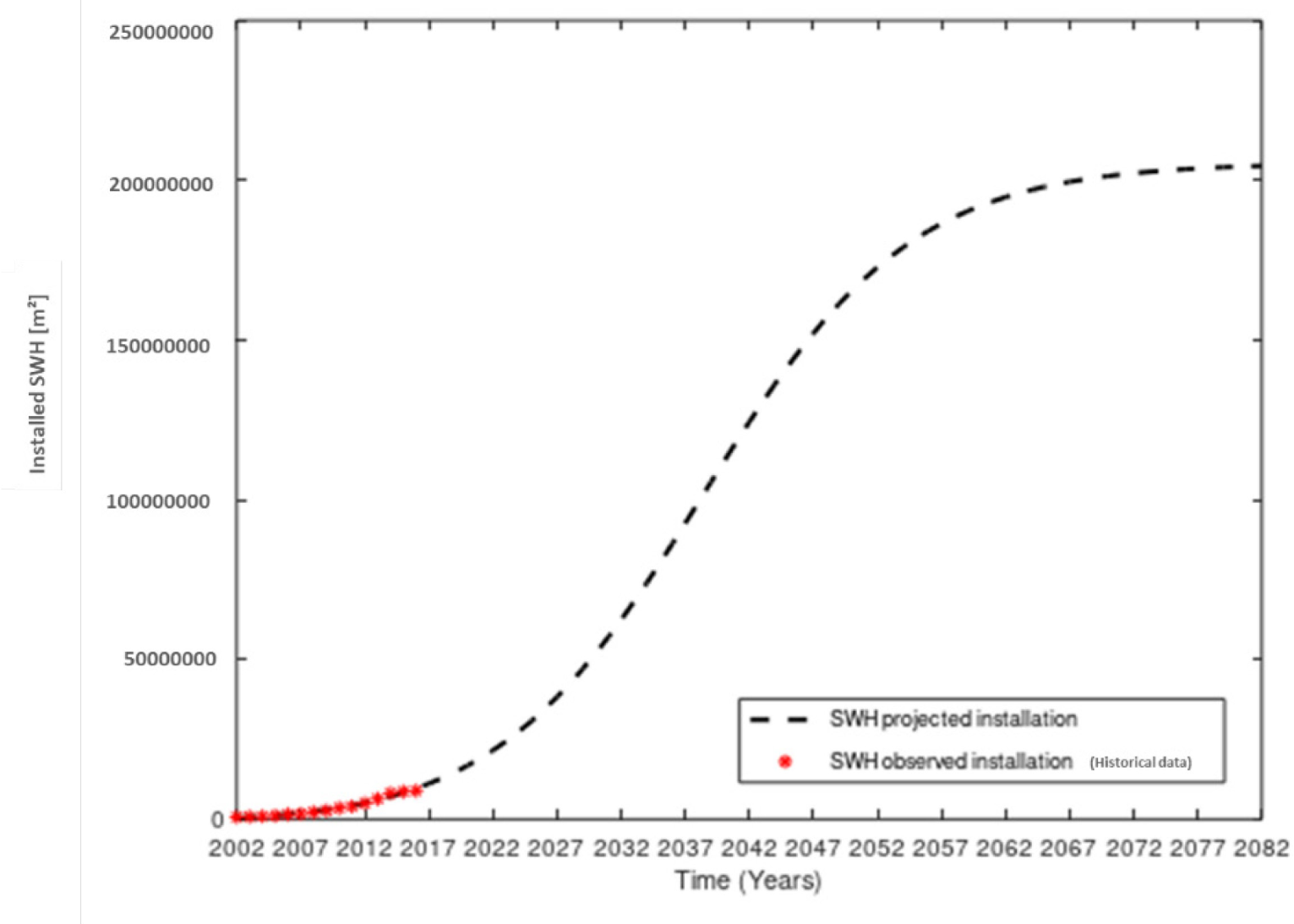
Figure 3 depicts how the SWH market is diffusing in India, considering the parameters obtained with historical data up to 2016 and the final potential market estimated by this methodology. The SWH market will converge to the final potential market after the year 2050. In the year 2016, the diffusion was still nearly 5% of the total final potential market, estimated at 205.46 million m². Estimations from the literature indicate that 100 million m² will only be achieved near the year 2030 [18]. This approach projects such a milestone after 2035, based on the historical data and the final potential market estimation.

Figure 3

Projection of SWH diffusion in India

In Figure 4, the parameters from the SWH market are used to project the diffusion of rooftop PV systems (total installed distributed household solar power) in the residential market in India, up to a final potential market estimated of nearly 140 GW in the whole country by this potential market methodology. The comparison is made of the diffusion when considering parameters obtained from a study in the USA [27] (black curve) and diffusion when the parameters are obtained from an SWH market (green curve).

Figure 4

Projection of the rooftop PV market evolution in India using parameters from PV data from USA and from SWH data

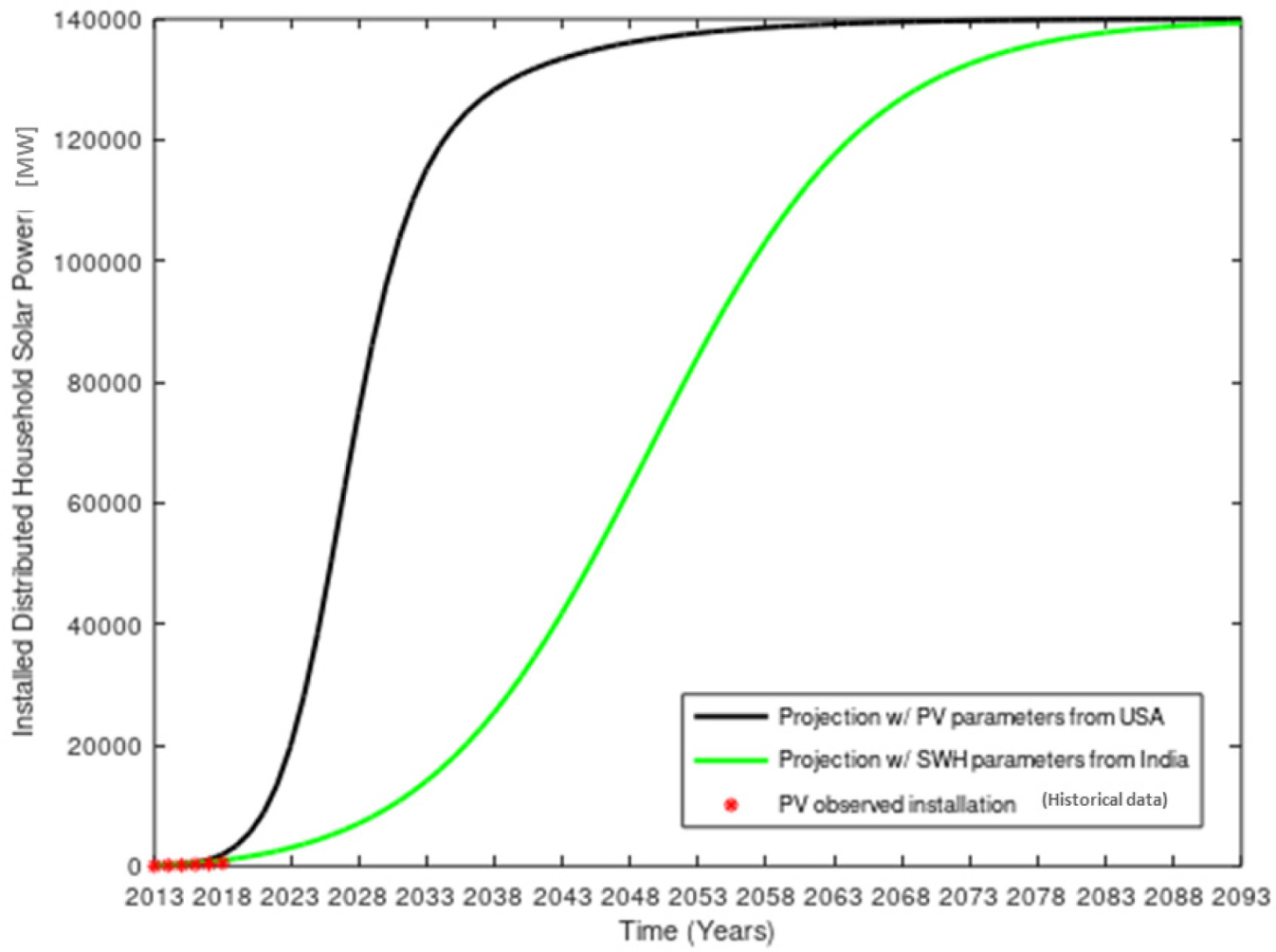
The rooftop PV diffusion is progressing slower in the coming years than that estimated for other PV markets like the USA [27], which presents a stronger initial diffusion. It is explained by the first initial results of residential rooftop PV diffusion in India, as shown highlighted in Figure 5, where the historical data (red dots) align better with the diffusion path (green curve) obtained with the local SWH data. This study corroborates more conservative projections observed in the literature for the Indian grid-connected solar PV market [18], in which cumulative installations will achieve 35 GW in the year 2030 [18]. Considering that currently, the percentage of residential installations (15%) is lower than in other parts of the world and tends to increase in the years to come, this number could range from 5 to 20 GW, which is inside estimations with SWH parameters p and q. Using Bass model parameters from the USA, it would be nearly 100 GW, far from what is projected in this paper.

Figure 5

Projection zoomed in the years 2013-2018 of diffusion; the vertical axis indicates Installed Distributed Household Solar Power [MW]

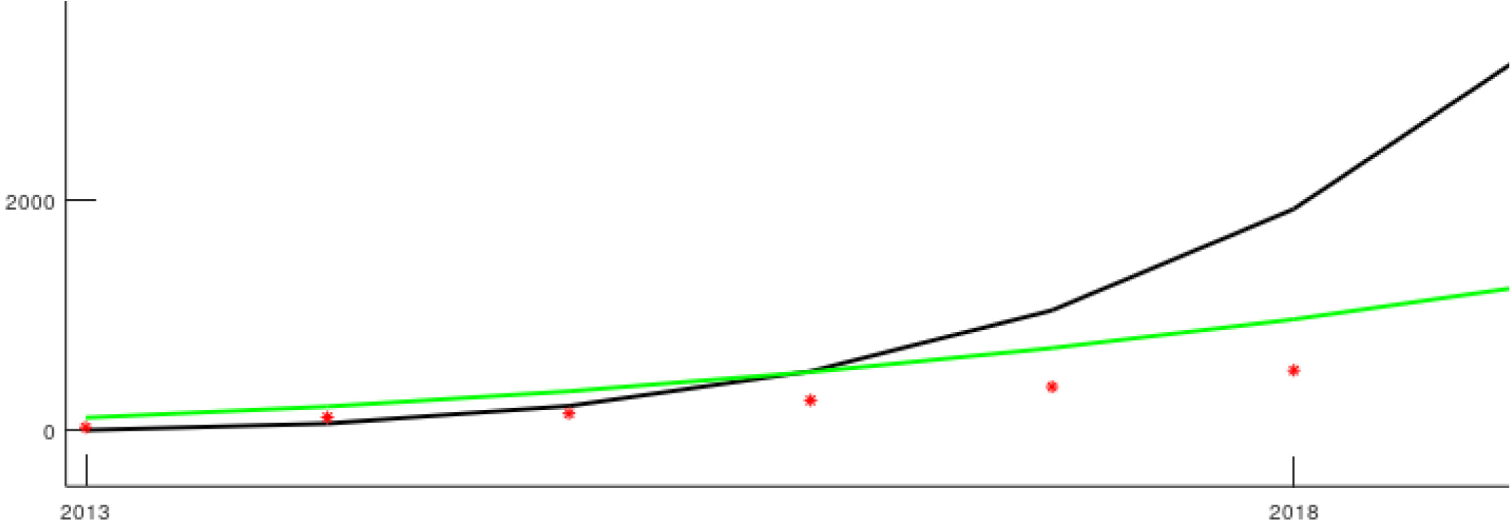
Considering that the similarities of SWH and rooftop PV markets are sufficiently strong to be used as a proxy, additional policies to foster PV technology could be necessary to accelerate rooftop PV diffusion in India and accomplish renewable energy goals. Also, the present research indicates that it would be possible to achieve 5-20 GW of residential installation by 2030. In contrast, the target of the National Solar Mission of India is to achieve 40 GW of rooftop PV (including industrial, public, and commercial installations along with residential) by 2022. This target seems difficult to achieve as the installed rooftop PV capacity in 2018 was 5.2 GW.

An initial estimation was presented of how rooftop PV will tend to diffuse in the years in a market where PV is also used as a primary source of electricity for local communities. India was used as a case study. The final potential residential rooftop PV market was estimated considering the total number of households. On the other hand, from the SWH historical data, technology diffusion parameters were estimated according to the Bass model approach. After borrowing the parameters from one market to another due to market similarities, these results show that PV diffusion in India will tend to be much slower than observed in other residential PV markets, like the USA if no additional incentives are considered in this market. Moreover, this diffusion might be even slower if PV technology is used as a primary source of electricity since it demands a parallel diffusion of other technologies, such as batteries.

Future work could explore different pathways: a comparison of different diffusion methodologies and a refinement of the potential market estimation methodology could be used to improve this approach’s estimation for India. Additionally, an estimation for the USA market using this approach could be another important path of validation of the methodology in a general approach.