The State of the Art in Model Predictive Control Application for Demand Response

Alqurashi, Amru

Under the patronage of:

Journal Metrics

Impact factor (2022): 2.1

Source Normalized Impact per Paper (SNIP): 0.532

SCImago Journal Rank (SJR): 0.42

The State of the Art in Model Predictive Control Application for Demand Response

DOWNLOAD FULL TEXT PDF

Review paper

Journal of Sustainable Development of Energy, Water and Environment Systems
Volume 10, Issue 3, 1090401
DOI: https://doi.org/10.13044/j.sdewes.d9.0401

Amru Alqurashi

Imam Abdulrahman Bin Faisal University, Dammam, Saudi Arabia

Abstract

Demand response programs have been used to optimize the participation of the demand side. Utilizing the demand response programs maximizes social welfare and reduces energy usage. Model Predictive Control is a suitable control strategy that manages the energy network, and it shows superiority over other predictive controllers. The goal of implementing this controller on the demand side is to minimize energy consumption, carbon footprint, and energy cost and maximize thermal comfort and social welfare. This review paper aims to highlight this control strategy's excellence in handling the demand response optimization problem. The optimization methods of the controller are compared. Summarization of techniques used in recent publications to solve the Model Predictive Control optimization problem is presented, including demand response programs, renewable energy resources, and thermal comfort. This paper sheds light on the current research challenges and future research directions for applying model-based control techniques to the demand response optimization problem.

Keywords: Stochastic MPC, robust MPC, energy management, demand response, renewable energy

Views (in 2024): 268 | Downloads (in 2024): 52
Total views: 2537 | Total downloads: 1065

INTRODUCTION

Many countries expressed the need to make their power infrastructure more cost-effective, environmentally clean, and sociologically acceptable, thus sustainable. A considerable amount of the generated power is currently being lost due to various technical reasons: a) separated generation from end usage, b) outdated transmission and distribution lines, c) missing demand-responsive technology and policy infrastructures. Also, the load congestion bottlenecks in the existing grid raise barriers to integrating renewable forms of energy. The situation is exacerbated by increasing load demands and historically declining research and development investment by power utilities. Moreover, the dependency on centralized power generation is expected to increase emissions and raise electricity tariff prices [1]. Distributed resources such as renewable energy sources (RES) and demand response (DR) programs reduce transmission congestion, carbon footprint, and electricity price. However, DR's uncertainties increase the complexity of integrating them into the existing power grid. Therefore, energy management using the DR programs gained a lot of attention in recent years. Energy management can achieve different objectives such as minimizing the cost, reducing greenhouse gases, and minimizing the loss of generation, transmission, and distribution systems [2], [3]. DR programs can improve flexibility in the power system's operation and facilitate the low carbon transition in electricity production. The main objective of demand-side management is to mitigate the power supply's uncertainty and fluctuation, creating electricity demand flexibility. This demand flexibility increases the ability to integrate large penetrations of renewable energy. In other words, demand-side management utilizes distributed generators, including RES, using DR programs. Also, DR has a very high potential to improve power systems' performance in terms of energy saving, energy cost, emissions, and integrated RES. According to Energy Technology Perspectives Clean Energy Technology Guide [4], utilizing DR increases distributed generators' participation in the electricity market, which encourages installing more RES on the demand side and, as a result reducing transaction costs. The global market for DR has received a lot of attention. The wholesale demand response capacity in the United States grew to 28 GW and 35 GW from the retailer programs. In Italy, a total DR capacity of 280 MW was commissioned, while in Ireland, 415 MW was awarded in a four-year-head-action. In Japan, 1 GW was offered through different DR programs, such as the Interruptible load DR program and incentive-based DR programs.

Figure 1

Demand side management classification

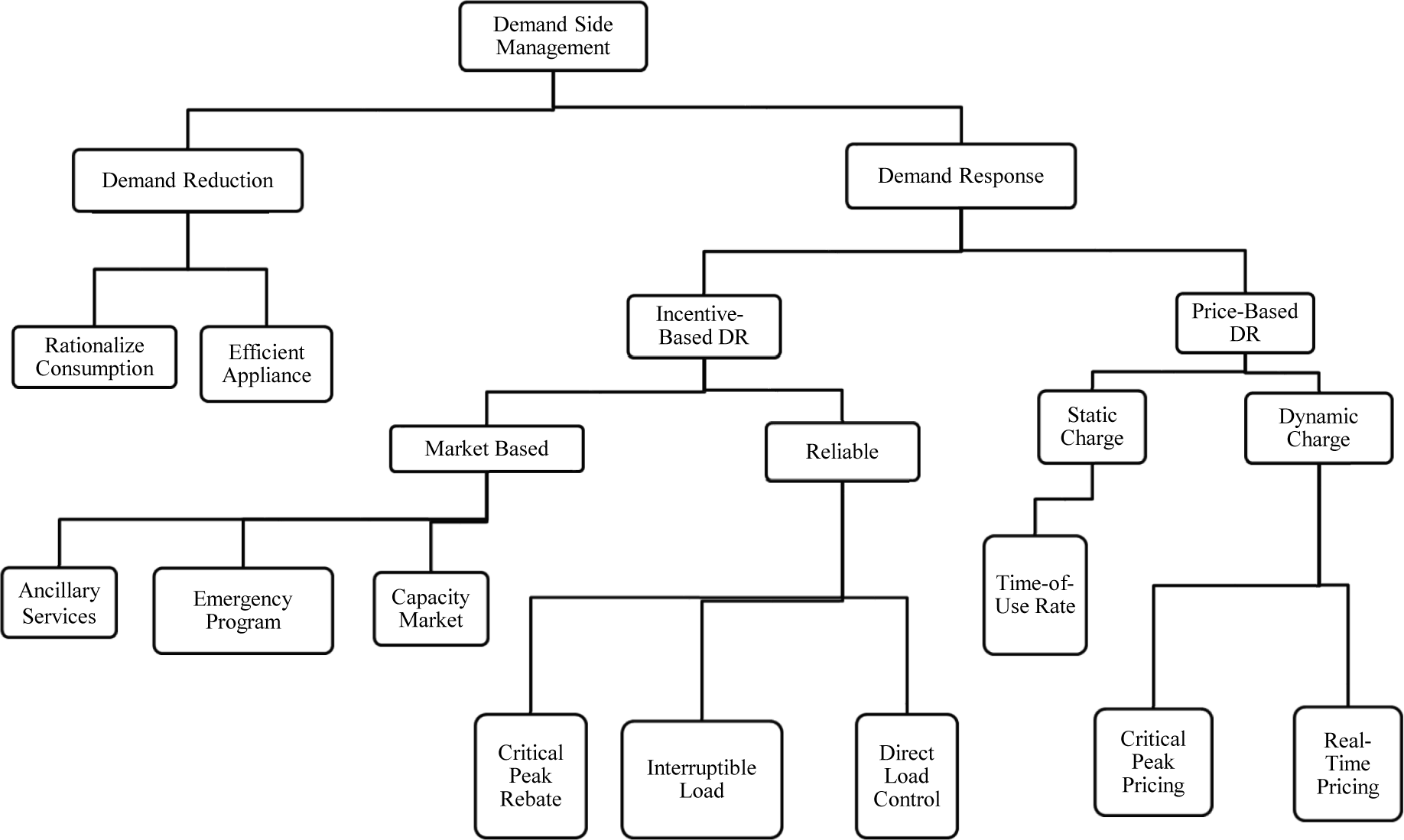
As shown in Figure 1, the demand-side management can be classified into a demand reduction and DR. The demand reduction achieves using efficient appliances or changing consumer behavior. On the other hand, the demand response program can be an incentive-based program (dispatchable) or a price-based program (non-dispatchable). With a specific contract, the incentive DR programs allow the independent system operator (ISO) to reduce customers' loads. There are different types of incentive DR programs that can be set up for the customer. Some of these types are [5]-[10]:

Direct load control (DLC): this gives the ISO direct control of the customer processes.
Interruptible load: a customer contract with limited sheds.
Emergency program: this allows the customers to respond to the emergency signal.

On the other hand, a price-based DR program influences customer consuming behavior by applying different tariffs throughout the day. There are different types of price-based DR program, some of which are:

Time-of-use rates: a scheduled fixed price.
Real-time pricing (RTP): the end customers have the wholesale price.
Critical peak pricing: a less predetermined variant of time or use.

Utilizing the full potential of DR programs needs a control system that manages the energy network. Different control strategies have been applied to manage the demand side, such as classical, soft, and hard control strategies [11] [12]-[14]. Classical control, such as PID, is integrated with a predictive algorithm to enhance its ability to manage the building energy system. Soft control uses historical data for controlling the system, while the hard controller uses a model to determine future modus operandi. A hard controller's ability to foresee the upcoming system variability makes it more adaptive to the change. One of the best examples of the hard controller that has been used in building energy management is Model Predictive Control (MPC). MPC technique can adapt and update the model by using a feedback signal. This feature of the MPC allows the system to be rationalized with the new estimation or the measurement. As a result, the ongoing interval will be optimized based on estimating the future time interval. MPC mitigates future uncertainty by predicting the direction of the future and optimize the current decision. Moreover, the fast response of the MPC and the ability to incorporate several control operations makes MPC suitable for energy management optimization problems.

Considering the uncertainties of the power systems in energy management optimization problems will increase the solution's optimality. The difficulty of solving a real-time optimization problem that considers the uncertainty of the energy management problem can be tackled by different optimization techniques. Different review articles have been published on control strategies of demand-side energy management problems. In [5], the authors focused on the intelligent control system that achieved a building's comfort level using different control strategies such as a fuzzy logic controller and a neural network controller. On the other hand, the authors in [15] focused their review on agent-based control and model-based predictive control. In [16], the authors reviewed the supervisory and optimal control of the Heating, Ventilation, and Air Conditioning (HVAC) system in a building. The review paper in [17] focused on MPC's HVAC system theory and applications. Reference [18] provided different building energy management strategies such as MPC, fault detection, stochastic optimization, and robust optimization for residential and non-residential buildings. Unlike the aforementioned reviews, this present paper mainly focused on the recent journal publications that showed the MPC approach's capability to handle demand response optimization problems considering a high uncertainty level. In other words, this paper tries to summarize algorithms and techniques that have been used in recent publications to solve MPC optimization problem that includes RES, thermal comfort and different type of DR. Based on the uncertainty level, the optimization problems can be formulated as deterministic MPC, stochastic MPC, scenario approach MPC, or robust MPC. A comparison between different type of MPC formulations and MPC optimization methods are conducted. Also, this paper classifies the recent publications in demand-side management based on MPC formulations.

This paper is organized as follows: Section 2 provides an overview of different MPC formulations: deterministic MPC, stochastic MPC, scenario approach MPC, and robust MPC. Section 3 reviews the existing literature on the application of MPC in managing the demand side, focusing on the demand response. Section 4 concludes the paper and presents future research directions.

MODEL PREDICITIVE CONTROL

MPC is an optimization-based control technique that aims to drive the closed-loop system to an optimal operation set-point while meeting state, input, and output constraints. Using the MPC feedback mechanism, the optimization problem inside the moving horizon window is solved at each time step. Only the first control action is implemented, and the rest is discarded. Therefore, MPC can predict the evolution of the states over the prediction horizon. However, modeling a building for MPC is time-consuming since each building has a specific model [19]. To prepare a building model for demand response using MPC, white-box, black-box, or gray-box model structures have been used in the literature. The white-box modeling is developed based on the system's physical process, while the black-box model is developed based on measuring the inputs and outputs of the system [20]. Gray-box modeling is a mix of white-box and black-box approaches. For example, reference [21] applied the white-box approach for modeling, while reference [22] utilized the block-box approach. Gray-box modeling is used in [23], [24]. In terms of the simulation tool, researchers use different software environments for modeling buildings, such as DYMOLA [25], TRNSYS [26], EnergyPlus [27], and ESP-r [28]. A review paper in building modeling techniques can be found in [29]. After modeling the building, the optimal control strategy, such as MPC, can be applied.

Depending on data uncertainty, different optimization methods, such as deterministic, stochastic, and robust optimization, have been used to the formulated energy management problem. In the deterministic MPC formulation, the uncertainty parameters are assumed to be time-independent parameters (perfect prediction). Therefore, the deterministic formulation is less complicated, which lowers the computational time of solving the optimization problem. However, the perfect prediction assumption of the uncertainties in the deterministic approach is not realistic, which may lead to a sub-optimal solution. On the other hand, the stochastic approach is more realistic since it considers the uncertainties in the decision-making process. Nevertheless, the stochastic approach's computational time is very high due to the complexity of the formulation. Since stochastic MPC requires prior knowledge of the underlying probability distribution function for the uncertainties, which is hard to find for complex processes, robust MPC is an alternative MPC paradigm that can deal with uncertainty without knowing the probability distribution. This paradigm can be achieved by deriving a robust invariant set of the error system, which is the difference between the real and nominal systems. To construct the invariant set, a feedback control law is used (e.g., LQR based control law and feedback linearization). The robust MPC can then optimize the process performance online while maintaining the close loop state within the stability region. However, deriving a robust invariant set can be challenging.

Several papers have compared deterministic and stochastic optimization methods for demand-side energy management problems [30]-[32]. References [30], [31] applied deterministic and stochastic MPC on a single room with an HVAC system, while reference [30] applied MPC and weather prediction in integrated room automation by controlling the HVAC system. The result of these studies showed that deterministic and stochastic MPC had similar performance in terms of energy use. The authors in [33] compare the deterministic and robust MPC method in a single room. The result showed the robust MPC outperforms the deterministic in case of high uncertainty consideration. Comparison of deterministic, stochastic, and robust MPC optimization methods are shown in Table 1 [34]-[44]. In the following subsection, the deterministic MPC schemes will be given. In the second and third subsections, stochastic MPC formulations that utilize the uncertainties' probabilistic measures will be presented. Finally, another form of MPC, famously known as robust MPC, will be provided.

Table 1

Comparison of MPC optimization methods

Optimization Methods	Reference	Complexity	Computational Speed
Deterministic MPC	[34], [35]
Simple	High	Low	Low
Stochastic MPC	[36]-[38]
More complexity in joint chance-constrained compared to recourse problems	It leads to a considerable size expansion of the problem and eventually increases the computational burden	Very good	Good
Scenario Approach MPC	[39], [40]
Choosing approximations and models is difficult	It is inversely proportional to the number of samples	It depends upon the size of the sampling	It is very good for a large number of samples
Robust MPC	[41]-[44]
Very complex	Slow	High	High

Deterministic model predictive control

The mathematical formulation of the deterministic MPC for the class of nonlinear continuous system is as follows [34]:

$\min_{u (t) \in S (Δ)} \int_{t_{k}}^{t_{k + N}} [\overset{⌣}{x} {(τ)}^{T} Q \overset{⌣}{x} (τ) + u {(τ)}^{T} R u (τ) d τ]$ (1a)

$s . t \tilde{x} (t) = f (\dot{\tilde{x}} (t), u (t))$ (1b)

$u (t) \in U, \forall t \in [t_{k}, t_{k + N}]$ (1c)

$\tilde{x} (t_{k}) = x (t_{k})$ (1d)

$x (t) \in X, \forall t \in [t_{k}, t_{k + N}]$ (1e)

where u(t) is the decision variable defined over the prediction horizon length N. The control objective is to minimize a quadratic function that penalizes the deviations of the predicted states and inputs from their corresponding set-points (equation (1a)). The nominal model of equation (1b) is applied to predict the process of state evolution over the prediction horizon. To mitigate a feedback control scheme, the predicted model is initiated at each sampling time t_k by the measured state from the real system x(t_k). The input constraints U and state constraints X are enforced over the entire prediction horizon. The above MPC formulation can be applied to nonlinear discrete systems by replacing the nominal model of equation (1b) by the nominal discrete system (i.e., x(k+1) = f_d (x(k), u(k), 0)) [35]. Up to this point, addressing the external disturbances and model uncertainties of the controlled process is not considered within the above deterministic MPC formulation. Such uncertainties will be taken into account via stochastic MPC paradigms, presented in the following subsection.

Stochastic model predictive control

A stochastic MPC algorithm can be developed using stochastic programming that can be reformulated as an optimal control problem considering the system's uncertainties. To understand how stochastic programming optimization problem is structured as an optimal control problem, the following stochastic discrete-time system is considered [36]:

$x_{t + 1} = f (x_{t}, u_{t}, w_{t})$ (2)

$y_{t} = h (x_{t}, u_{t}, v_{t})$ (3)

where t ∈ N, x, and u are the state and input vectors, respectively. The disturbance vector w and v can represent a wide range of uncertainties with known probability distributions. The term f is the function that describes the system dynamics, while h is the function that describes the outputs. For full state-feedback control, the N-stage feedback control policy for stochastic MPC can be defined as follows:

$π : = [π_{0} (.), π_{1} (.), \dots π_{N - 1} (.)]$ (4)

where π(.) is the Borel-measurable function for all i = 0...N-1. The stochastic discrete-time system can be formulated as a finite moving-horizon optimal control problem. By applying the MPC feedback mechanism, the value function of the resulting stochastic optimal control is commonly defined as follows:

$V_{N} : = E_{x t} [\sum_{i = 0}^{N - 1} J_{c} ({\tilde{x}}_{i}, u_{i}) + J_{f} ({\tilde{x}}_{N})]$ (5)

where J_c and J_f are the stage cost function and the final cost function, respectively. Given the initial states, the term \tilde x_i represents the predicted states at the time i. The objective function (equation (5)) is usually subjected to chance constraints. Using the conditional probability Prxt, the joint chance constraint over the prediction horizon formulation as follows [45], [46]:

$\Pr_{x t} [g_{i} ({\tilde{y}}_{i}) \leq 0, \forall j = 1, \dots, s] \geq β, \forall i = 1, \dots, N$ (6)

where g_i is the Borel-measurable function, ${\tilde{y}}_{i}$ is the predicted outputs at time i. s represents the number of inequality constraints, and the probability lower bound is represented by ?. By using value function (equation (5)) with joint chance constraints (equation (6)), the stochastic optimal control problem for the stochastic discrete-time system (2-3) can be formulated as follows [39], [40]:

$V_{N}^{o} : = \min_{π} V_{N} (x_{t}, π)$ (7)

Subject to:

$\begin{matrix} x_{i + 1} = f (x_{i}, u_{i}, w_{i}) & \forall i \in Z_{[0, N - 1]} \\ y_{i} = h (x_{i}, u_{i}, v_{i}) & \forall i \in Z_{[0, N]} \\ P r_{x t} [g_{i} ({\tilde{y}}_{i}) \leq 0, \forall j = 1, \dots, s] \geq β & \forall i \in Z_{[1, N]} \\ w_{i} ~ P_{i} & \forall i \in Z_{[0, N - 1]} \\ {\tilde{x}}_{0} = x_{t} & \forall i \in Z_{[0, N - 1]} \end{matrix}$

where V^o_N is the function that represents the optimal value under the feedback control policy ρ(0). The optimal control sequence is implemented in a receding-horizon fashion (i.e., the first element of the optimal sequence π* is only applied between two consecutive time instants). Stochastic MPC is an optimal control scheme that aims to balance the trade-offs between fulfilling the overall control objectives and ensuring the satisfaction of the probabilistic constraints resulted from the uncertainty [36]-[38].

Scenario approach model predictive control

The scenario approach can be used to reformulate the stochastic optimization programming problem into a deterministic equivalent problem. To illustrate, a two-stage stochastic linear programming is used as an example. In two-stage stochastic programming with recourse, the decision-maker can take corrective actions (recourse decisions) after realizing the uncertainty over sequence stages. A general formulation for a two-stage stochastic linear programming with linear constraints is given by [47]:

$\min f (x) + E [Q (x, ω)]$ (8)

Subject to

$A x = b, x \in X$ (9)

where Q(x,ω) is the second stage optimal objective value

$Q (x, ω) = \min g (x, y, ω)$ (10)

$W_{ω} y_{ω} + T_{ω} x = h_{ω}, y_{ω} \in Y$ (11)

where ω is the probability distribution of the uncertain data for the second-stage, x represents the first-stage decision variable, and y represents the decision variable of the second-stage with the recourse action cost. E_ω is the optimal objective value expectation of the second-stage decision variable. Q(x, ω) represents the recourse action cost. W_ω represents the compensation of the system's variation of the T_x ≤ h_ω. To overcome the difficulty of obtaining the random variable's probability distribution function, the continuous probability distribution can be approximated using a finite scenario set (s) with their probabilities (π_s). As a result, the two-stage stochastic programming problem can be reformulated as a deterministic equivalent problem as follows:

$\min f (x) + \sum_{S \in S} π_{s} q_{s}^{T} y_{s}$ (12)

Subject to

$A x = b$ (13)

$W_{ω} y_{ω} + T_{ω} x = h_{ω}, y_{ω} \in Y$ (14)

To apply the MPC algorithm, the deterministic optimization problem can be formulated as an optimal control problem. To have an accurate solution to the optimization problem, a large number of scenarios have to be generated to represent the system's uncertainties. However, including a high number of scenarios raises the computational time or causes an intractable problem. Different approaches have been used to overcome this issue [48]. One way to reduce the computational time is to apply scenario reduction techniques [49], [50], which reduces the number of scenarios. As a result, the computational time is reduced, whereas the solution accuracy is compromised. Another way to circumvent the issue of a high number of scenarios is by using an online MPC algorithm [51]-[53].

Robust model predictive control

The decision in the robust optimization can be a one-stage decision that has to be taken before the uncertainty is realized, and no corrective action can be taken after the realization of the uncertainty. The robust optimization can also be formulated as multiple stages, where the decision can be taken depending on the flow of the uncertainty realization. It is worth noting that it is challenging to incorporate the dynamic of the uncertainty in the robust optimization [54]. The general robust optimization formulation is [55]:

$\min f_{o} (\bar{x}), S . t . f_{i} (\bar{x}, {\bar{u}}_{i}) \leq 0, i = 1, 2, \dots m$ (15)

where $f_{o} (\bar{x})$ is the objective to be optimized, and $f_{i} (\bar{x}, {\bar{u}}_{i})$ is the system constraints. f₀ and f_i are R_n →R functions. x is a vector of decision variables, and ${\bar{u}}_{i}$ is the parameter uncertainties of the uncertainty set (U_i). m is the number of uncertain parameters. A comprehensive survey of robust optimization can be found in [56]. The robust optimization problem can be formulated as a robust MPC optimization problem, iteratively over a finite-moving horizon window. In other words, given the initial state, the state-feedback control law is used to minimize the worst-case scenario subjected to control input and output constraints [57]. The summary of the formulations of MPC optimization methods is shown in Table 2.

Table 2

Formulations of MPC optimization methods

Optimization Methods	Objective Function	Constraints
Deterministic MPC	$\min_{u (t) \in S (Δ)} \int_{t_{k}}^{t_{k + N}} [\tilde{x} {(τ)}^{T} Q \overset{⌣}{x} (τ) + u {(τ)}^{T} R u (τ)] d τ$	$\begin{array}{l} \tilde{x} (t) = f (\dot{\tilde{x}} (t), u (t)) \\ \begin{matrix} u (t) \in U, \forall t \in [t_{k}, t_{k + N}] \\ \tilde{x} (t_{k}) = x (t_{k}) \end{matrix} \\ x (t) \in X, \forall t \in [t_{k}, t_{k + N}] \end{array}$
Stochastic MPC $V_{N}^{0} : = \min_{π} V_{N} (x_{t}, π)$	$\begin{array}{l} \begin{matrix} x_{i + 1} = f (x_{i}, u_{i}, w_{i}) & \forall i \in Z_{[0, N - 1]} \\ y_{i} = h (x_{i}, u_{i}, v_{i}) & \forall i \in Z_{[0, N]} \\ \Pr_{x t} [g_{i} ({\tilde{y}}_{i}) \leq 0, \forall j = 1, \dots, s] \geq β & \forall i \in Z_{[1, N]} \\ w_{i} ~ P_{i} & \forall i \in Z_{[0, N - 1]} \\ {\tilde{x}}_{0} = x_{t} & \forall i \end{matrix} \\ \in Z_{[0, N - 1]} \end{array}$
Robust MPC	$\min f_{o} (\bar{x}),$	$f_{i} (\bar{x}, {\bar{u}}_{i}) \leq 0, i = 1, 2, \dots m$

DEMAND SIDE MANAGEMENT VIA MODEL PREDICTIVE CONTROL

Buildings account for 40% of our worldwide energy consumption [58], [59]. Therefore, the need for controlling building energy consumption has received much attention. Many researchers investigate the potential of reducing electricity bills and greenhouse gases by optimizing energy usage in a building [60], [61]. According to [62], up to 35% of energy could be saved by selecting an optimal temperature set-point. Also, using the internet of energy technology is substantial for managing the energy network in a building. Internet of energy facilitates monitoring and controlling the flow of information between sources and loads. Taking advantage of the internet of energy technology, the fast ability to feed the control system with updated information helps the controller algorithm make an optimal decision [63]-[65]. As a result of this technology, many researchers applied the MPC technique on building energy management systems and showed that the MPC has better performance over other controllers in terms of transient and steady-state responses. Also, the MPC approach provides the ability to account for multivariable control action, which can be applied to optimize generation and demand response. MPC is considered one of the best control strategies for optimizing the energy flow within a building due to its inherent advantages, such as anticipatory control actions, handling uncertainty, and the time-varying system. MPC techniques can incorporate energy conservation strategies and disturbance rejection in its algorithm [17] [66]. However, there are several challenges when MPC is implemented, such as control design and building modeling. The decision to use the MPC strategy for a building mainly depends on its cost and performance [67].

In general, the controller's goal in a building energy management system can be categorized as follows. 1) minimize the operational cost, 2) maximize the utilization of RES, 3) achieve thermal comfort level by using a minimal amount of energy. 4) minimize the peak load or reschedule it. To achieve the control goal using MPC strategies, an optimal control optimization problem has to be formulated to minimize an objective function considering several constraints. The objective is usually to minimize the energy cost, but multi-objectives can minimize the cost and guarantee thermal comfort. Also, time-dependent constraints can be used for different comfort levels. Constraints can also be constructed to limit some of the parameters. Various Constraints can be considered in the MPC, such as equipment, energy match, economic, environmental, and political constraints.

Figure 2

Smart home energy management

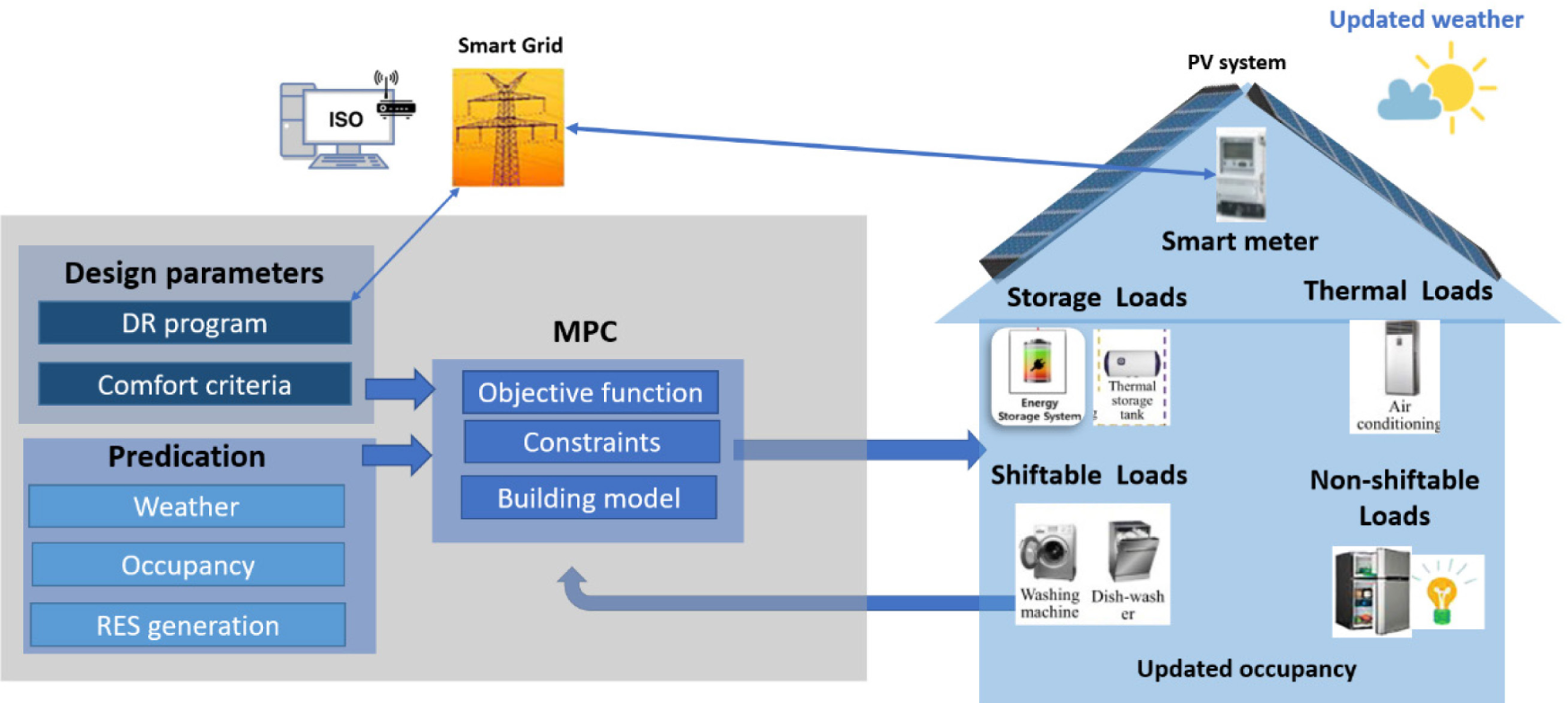
Figure 2 illustrates the basic methodology of MPC for a building. The design parameters and predicted disturbances are the inputs to the MPC. Considering these inputs, the MPC optimizer minimizes the objective function is subjected to the constraints and the dynamic of the building model. Using the feed mechanism, the MPC controller applied only the first step of the solution and discarded the rest. In each time step, the MPC is updated with the current states. Based on the DR program, the MPC controller can manage the different types of loads to minimize energy costs. For example, the storage loads and the shiftable loads can be feed during the off-peak hours, where the electricity price is low.

As previously discussed, the MPC formulation can be categorized into deterministic MPC, stochastic MPC, scenario approach MPC, and robust MPC. The main difference in these formulations is how the system's uncertainties are considered on the optimization problem. Researchers used all these formulations to develop an MPC algorithm that can manage the building's energy system. Regardless of the MPC formulation, the MPC algorithm's implementation can be centralized, decentralized, distributed [68], [69]. Table 3 summarizes the techniques and evaluation of recent publications' contributions to utilizing RES, thermal comfort, cost reductions, shaving, shifting, or shaping load peaks for buildings' energy consumption, and characteristics of the demand response [30], [32], [70]-[107].

Table 3

MPC formulations for demand-side energy management

Formulation	Ref	Techniques	Utilized RES	Thermal Comfort	Reduce Cost	Load Peak	DR
Deterministic MPC	[70]	EMPC	No	No	Yes	Shaving 26%	TOU
	[71]	Mixed-Integer Nonlinear Programming, EMPC	PV	Yes	Yes	Shifting	Price-Based.
	[72]	Artificial Neural Networks Dynamic Programming	Wind	Yes	Yes	Shaping	Control Load
	[73]	MINLP Branch …Bound Algorithm	No	Yes	Yes	Shaving	Auxiliary Services
	[74]	Cluster Analysis	PV	Yes	Yes	Yes	DLC
	[75]	Proposed Algorithm	PV	Yes	Yes	Shaving %23	Ancillary Services
	[76]	Mixed-Integer Linear Programming	PV	No	7%	Shaving	TOU
	[77]	Linear State-Space Model, Discretized	Wind	No	Yes	Shaving	Dispatchable
	[78]	Quadratic Program	No	Yes	Yes	Shaving	No
	[79]	Exponentially Weighted Moving Average Algorithm	Yes	Yes	Yes	Shifting	DCL
	[80]	Linear Quadratic Method Monte Carlo	No	Yes	Energy Saving 43%	Shaving	No
	[81]	Linear Quadratic Method Monte Carlo	No	Yes	Energy Saving 43%	Shaving	No
	[82]	Mixed-Integer Programming	Solar Thermal	Yes	Yes	Shifting	Price-Based
	[83]	Cooperative Optimization, EMPC	No	Yes	15%	Shifting	No
	[84]	Discrete Quadratic Programming	No	No	Yes	Shifting	Incentive-Based
	[85]	Adaptive Approach	Wind, PV	Yes	46%	Shaving	TOU
Stochastic MPC	[30]	Probabilistic Constraints Factorial Simulation	No	Yes	Yes	No	No
	[32]	Discrete Algorithm Sampling Algorithm	No	Yes	Yes	Shaving	No
	[86]	Monte Carlo Probabilistic Constraints	PV	Yes	Yes	Shafting	DCL
	[87]	Monte Carlo Probabilistic Constraint	No	Yes	Yes	No	No
	[88]	Probabilistic Time-Varying Constraint	No	Yes	Yes	Shaving	Incentive-Based
	[89]	Two-Stage Optimization Discrete	No	No	7.5%	Shifting	Price-Based
	[90]	Quadratic Programming	No	No	Yes	No	No
Scenario Approach MPC	[91]	Discrete, Markov Chain, Monte Carlo	Wind	No	12%	Shifting	DCL
	[92]	Probabilistic Monte Carlo	Solar	Yes	20%	Ramp Shaving 50%	RTP
	[93]	Probabilistic Gaussian Distribution	No	Yes	Yes	Shifting	RTP
	[94]	Mixed-Integer Linear Programming	Solar	Yes	25%	No	Price-based
	[95]	EMPC Stochastic State Space	No	Yes	Yes	Shifting	TOU
	[96]	EMPC Probabilistic, Scenario	No	No	9-32%	Shaving	RTP
	[97]	Sequential Linear Programming, EMPC	Wind, PV Solar	Yes	21%-75%	Shifting	Price-Based
	[98]	Probabilistic Search	No	Yes	Energy Savings 35%	Shaving	Incentive-Based
	[99]	Neural Network Predictive Control	Wind PV	No	Yes	Shaving	Reliability
Robust MPC	[100]	Fuzzy Model	No	Yes	Yes	Yes	No
	[101]	Quadratic Programming	No	Yes	Yes	Shaving	Incentive-Based
	[102]	Mixed-Integer Linear Programming	No	Yes	yes	Shifting	TOU
	[103]	EMPC, Decomposition Control Variables	PV	No	No	yes	No
	[104]	EMPC, Min-max Worst Case Approach	PV	No	Yes	Yes	Price-Based
	[105]	Adaptive Robust MPC	No	Yes	Energy Savings 20%	Shaving Shifting	Real-time- Based
	[106]	Robust Constraints Satisfaction	No	Yes	yes	Shifting	No
	[107]	Linear Matrix Inequalities	No	Yes	Yes	Shifting	Price-Based

Deterministic model predictive control in demand response

The uncertainty parameters usually come from solar irradiation, occupancy, RES, and weather forecast in the energy management optimization problem. These uncertainty parameters are assumed to be time-independent parameters in the deterministic MPC approach. A vast body of literature applied deterministic MPC to manage energy networks in a building [70]-[79]. Table 3 shows the techniques and controller objectives for each reference that applied the deterministic MPC approach.

A group of publications [70], [73], [77] used the hot water system in a building as an energy storage system. Based on the DR, the authors in [70] used an EMPC controller that optimized hot water system consumption by determining the optimal set-point of water temperature. Reference [77] proposed an MPC controller scheme that aggregated electric water heaters and provided the ISO with ancillary services. Also, the authors in [73] proposed an MPC controller scheme that aggregated thermostatically controlled appliances and provided them to the ISO as ancillary services.

A few publications [71], [72], [74], [75], [79] have directly dealt with the issue of the generation intermittency of renewable energy by using DR programs. References [79] and [74] used the DLC program to balance the renewable generation fluctuation by applying distributed and centralized MPC algorithms. The authors in [79] control the HVAC and the water level to shape the load while [74] controls the thermostat set-points for air conditioners. Reference [75] developed an MPC framework that optimizes the interaction between renewable generation and the battery storage system while maintaining the comfort level and reducing peak load. The authors in [72] proposed an MPC strategy to reduce the fluctuation of wind energy by regulating grid consumption and on-site energy generation and controlling the elastic loads. By modeling the building's behavior and weather forecasting, [71] proposed an EMPC controller that can match demand with fluctuations in supply.

In [76], MPC based on a deep reinforcement learning method was used to utilize dispatchable loads and storage resources in a DR program. A prototype was installed to demonstrate the performance of their control method using the internet of things devices. In [78], a machine learning technique for MPC was applied to minimize energy usage and guarantee the end-user comfort level. Using machine learning reduced the hardware and software complexity of the controller and, as a result, the implementation cost. Experiments were conducted in [80], [81] to show the MPC performance's superiority to minimize energy consumption while maintaining comfort. Reference [82] proposed a nonlinear model predictive controller that optimizes the energy usage and comfort level based on a linear thermal model, which reduces the problem complexity, resulting in reducing the computational time.

Stochastic model predictive control in demand response

In building energy management, researchers have used stochastic MPC formulation to include uncertainties such as occupancy, ambient temperature, solar radiation, and renewable energy generation. Table 3 shows the techniques and controller objectives for each reference that applied the stochastic MPC approach. In contrast with the deterministic approach, the stochastic MPC considers the uncertainty in the decision-making process. To include uncertainties in the DR optimization problem, chance-constrained is usually used in a stochastic MPC algorithm. For instance, reference [86] proposed a chance-constrained MPC to take into account the uncertainties of ambient temperature and PV generation. The developed model optimizes the scheduling of the controllable appliances based on energy cost, thermal comfort, and PV system. Chance constraints can be transformed into deterministic using a sample-based method and discrete convolution integrals, as shown in [32]. This reference considers the uncertainties of occupancy loads and weather and used stochastic MPC to control small-scale HVAC systems while guaranteeing the occupancy's comfort level. However, using chance constraints on a large system sometimes leads to computational intractability issues. To overcome this problem, the authors in [87] developed a closed-loop disturbance feedback formulation to reduce the conservatism of the problem. This reference used Monte-Carlo simulations to validate the chance-constrained solution. The stochastic algorithm was capable of considering the weather forecast and ensure temperature preferences and DR requests. The authors in [30] and [88] focused on including weather prediction uncertainty in the stochastic MPC to increase energy efficiency and maintain the thermal comfort level. The authors compared the predictive controller and rule-based controller with a stochastic MPC controller, which outperforms both controllers. A recent publication [89] compared deterministic and stochastic MPC of HVAC plants and showed that the deterministic solution fails to capture uncertainties, resulting in economic penalties. On the other hand, the stochastic MPC approach was more prepared to handle the uncertainties, leading to cost savings.

Scenario approach model predictive control in demand response

Stochastic MPC based on chance constraints is difficult to be solved. Therefore, some researchers use a scenario approach to reformulate the stochastic MPC optimal problem to a deterministic equivalent problem. Table 3 shows the techniques and controller objectives for each reference that applied the scenario approach MPC. The system's uncertainty can be captured using a sampling method based on the probability distribution function [108].

The Monte-Carlo technique is commonly used to sample a probability distribution randomly. Applying the Monte-Carlo technique, reference [91] used energy storage as a DR to shave the load and reduce wind generation fluctuation. In this reference, the wind generation and customer behavior uncertainties were considered in the scenario-based MPC to maximize social welfare.

Another approach to include the uncertainty in MPC algorithms is using the Markov chain modeling framework. For instance, the wind power uncertainty was modeled in [91] using the Markov chain Monte-Carlo method.

The high penetration of renewable resources increases the probabilistic variations of power generation. These probabilistic variations can be handled using energy storage systems and DR programs. However, some of the DR programs may increase the system's uncertainty due to the customer's behavior. Therefore, the online MPC approach can be more adaptable to the probabilistic variations of the model and enhance the solution's accuracy [91], [92], [99].

A real-time optimization framework MPC can utilize thermal mass storage and energy storage systems to control power flow between the grid, a PV system, and a commercial building [92]. Reference [99] developed a real-time MPC algorithm based on a neural network technique that manages the energy system in a zero-energy building.

Considering the uncertainties of the model, such as solar irradiation, occupancy, renewable energy resources, and weather forecast, the energy management stochastic optimization problems are formulated to minimize the operational cost of integrating renewable energy resources, DR, and controllable, and storage devices Figure 2 [93]-[98]. The authors in [93] took advantage of a commercial building's flexible operation and proposed an MPC strategy that considered real-time pricing and thermal comfort level. To increase the model's accuracy, the authors consider the uncertainty of cooling demands in their stochastic optimization problem. In [92], the authors applied MPC to optimize the HVAC system and the storage devices considering thermal comfort constraints and external temperature uncertainty. Reference [95] investigated the EMPC strategy's ability to utilize a high penetration of renewable energy in the system to reduce the operational cost and maintain the system's reliability. On the other hand, reference [96] applied EMPC on supermarket refrigeration systems, which enable it to be used as ancillary services. In [95], the authors used sequential linear programming to achieve an EMPC strategy that reduces computational time and minimizes the energy cost significantly. In contrast, the authors in [98] used cloud parallel computation to consider the full complexity simulation in the proposed MPC algorithm.

Robust model predictive control in demand response

The robust optimization deals with the range or region of a deterministic uncertainty while taking into account the worst-case scenario over the predetermined deterministic uncertainty set. Since robust optimization does not need probability distribution, it is preferable when the probability distribution is difficult to obtain from uncertain data. The robust optimization approach uses an uncertainty set that covers all the possible outcomes of the uncertain parameters. Thus, the optimality and feasibility of a solution are guaranteed within any realizations of the uncertainty set. Therefore, the uncertainty set must be carefully constructed to guarantee computational tractability. The objective is to find the optimal solution considering the worst-case scenario; hence, there is no need to include a large number of scenarios, like in the case of stochastic programming. Considering the worst-case scenario increases the reliability of solutions but leads to very costly (conservative) solutions. Therefore, by adding a constraint to the uncertainty set, a trade-off between the cost and reliability can be optimized [109], [110].

Due to the conservative solution and the implementation complexity of robust MPC optimization [111], a few researchers have applied robust MPC to the DSM optimization problem. Table 3 shows the techniques and controller objectives for each reference that applied the robust MPC. The authors in [101] formulated a min-max robust optimization problem taking into an account comfort level, controllable load, and electricity price. Considering the uncertainties of load predictions and ambient temperature, authors in [100] applied a fuzzy interval model to define the uncertainty bounds in the robust MPC formulation. The authors in [102] formulate a robust MPC optimization problem that optimizes multiple energy forms considering source-network-load flexibilities. In [103], [104], the authors propose a robust MPC that guarantees an optimal energy dispatch in a smart micro-grid considering bounded demand uncertainty. An adaptive robust MPC is presented in [105] to perform online estimation of uncertain parameters of the building, while the adaptive robust MPC proposed in [106] relies on recursive set membership identification to updated the close-loop operation in each time step. Robustness analysis to state estimation for a hybrid ground coupled heat pump system is applied in [107] using robust MPC. The result shows that robust method did not improve the state estimation for the investigated system.

CONCLUSION AND FUTURE DIRECTIONS

A smart grid advances two-way communication between the generation and end-users. This advancement of smart grid communication technologies allows consumers to participate in the electricity market through DR programs. Various DR programs have been used to optimize the participation of the demand-side. Utilizing the full potential of DR programs needs a control system that manages the energy network. Different methods of controlling techniques have been applied to manage the demand response in the literature. This paper provides a review of different MPC formulations, which are deterministic MPC, stochastic MPC, scenario approach MPC, and robust MPC. The deterministic MPC approach has the lowest computational time and most straightforward formulation comparing to other approaches. However, the perfect prediction assumption for the uncertainties may lead to a sub-optimal solution. The stochastic MPC approach considers the uncertainties in the decision-making process, resulting in a more realistic solution. The significant challenges of the stochastic approach are computing time and obtaining the probability distribution of the random variables. On the other hand, robust MPC deals with uncertainty without knowing the probability distribution by constructing an uncertainty set, which leads to a robust solution. However, the robust MPC solution is very costly since it considers the worst-case scenario.

The demand-side management optimization problems are subject to various uncertainties, including weather forecast, solar irradiation, occupant thermal comfort level, and electricity price. The high penetration of renewable distributed generation, such as wind and solar, has added additional uncertainties in the demand side due to the renewable energy sources fluctuations. However, these fluctuations can be mitigated by using an energy storage system. Smart grid capabilities also facilitate the utilization of the demand response programs to handle the demand side's uncertainties. Utilizing DR programs can increase power system reliability, reduce energy consumption, and minimize operational costs. To this end, an MPC strategy considers design parameters and predicted disturbances to come up with optimal control actions that maximize social welfare. Since the computing power has been improving, recent publications focus on including the uncertainties of the system in the MPC formulation. The main research challenge is how to optimize the energy flow and cost, considering the variability of the renewable energy, weather forecast, solar irradiation, thermal comfort, DR programs, and emission constraints. Most of the researchers applied the stochastic approach and considered some of these constraints. A few researchers used robust MPC since it generates a conservative solution.

The objective of implementing MPC on the demand side is to minimize energy consumption, carbon footprint, and energy cost; and maximize thermal comfort and social well-fare. However, several challenges can face researchers when considering the MPC in the demand response optimization problem. These challenges can be summarized as follows:

Modeling a building for MPC implementation.
Considering all kinds of uncertainties, such as weather prediction, RES, DR programs, and occupancy, in one model.
Reducing the computational time to solve the optimization problem.
Affordability and availability of the communication infrastructure to collect system measurements.
Handling big data that is collected from the system.

These challenges cause an observable discrepancy in the simulation results in the publications. A comprehensive model that considers all these challenges is needed. Taking advantage of smart grid technologies and cloud computing, artificial intelligence, and machine learning combined with MPC strategy has the potential to overcome these challenges and provide a cost-effective solution and ensure the security and reliability of the power system.

NOMENCLATURE

Abbreviations
DCL	Direct Control Load
DR	Demand Response
DSM	Demand Side Management
EMPC	Economic Model Predictive Control
ESS	Energy Storage System
HVAC	Heating, Ventilation, and Air Conditioning
ISO	Independent System Operator
MILP	Mixed-Integer Linear Programming
MINLP	Mixed-Integer Nonlinear Programming
MPC	Model Predictive Control
R…D	Research and Development
RES	Renewable Energy Sources
RTP	Real-Time Pricing
TOU	Time of Use
Variables
u(t)	Decision variable for the class of nonlinear continuous system
x̃(t)	State variable for the class of nonlinear continuous system
x_t	State vectors for the stochastic discrete-time system
u_t	Input vectors for the stochastic discrete-time system
W	Disturbance vector can represent a wide range of uncertainties with known probability distributions for the stochastic discrete-time system
v	Disturbance vector can represent a wide range of uncertainties with known probability distributions for the stochastic discrete-time system
X	First-stage decision for the two-stage stochastic linear programming
y	Second-stage decision for the two-stage stochastic linear programming
ω	Probability distribution of the uncertain data for the second-stage
x̅	Vector of decision variables for the robust optimization formulation
u̅_i	Parameter uncertainties of the uncertainty set for the robust optimization formulation

Kirschen

Strbac

Transmission networks and electricity markets

Fundamentals of power system economics 2004

141-204

https://doi.org/10.1002/0470020598.ch6

Alam

M.S

Arefifar

S.A.

Energy Management in power distribution systems: review, classification, limitations and challenges

IEEE Access 2019 7

92979-93001

https://doi.org/10.1109/ACCESS.2019.2927303

Rafique

S.F

Jianhua

Energy management system, generation and demand predictors: a review

IET Generation, Transmission … Distribution 2017 12 3

519-530

https://doi.org/10.1049/iet-gtd.2017.0354

IEA

Demand Response IEA

Paris

https://www.iea.org/reports/demand-response

2020

Vardakas

J.S.

Zorba

Verikoukis

C.V.

A survey on demand response programs in smart grids: Pricing methods and optimization algorithms

IEEE Communications Surveys … Tutorials 2014 17 1

152-178

https://doi.org/10.1109/COMST.2014.2341586

Palensky

Dietrich

Demand side management: Demand response, intelligent energy systems, and smart loads

IEEE transactions on industrial informatics 2011 7 3

381-388

https://doi.org/10.1109/TII.2011.2158841

Scheller

Provoking residential demand response through variable electricity tariffs-a model-based assessment for municipal energy utilities

Technology and Economics of Smart Grids and Sustainable Energy 2018 3 1

https://doi.org/10.1007/s40866-018-0045-x

Parrish

Heptonstall

Gross

The potential for UK residential demand side participation

System Architecture Challenges: Supergen+ for HubNet 2016

Uddin

A review on peak load shaving strategies

Renewable and Sustainable Energy Reviews 2018 82

3323-3332

https://doi.org/10.1016/j.rser.2017.10.056

Meyabadi

A.F

Deihimi

M.H.

A review of demand-side management: Reconsidering theoretical framework

Renewable and Sustainable Energy Reviews 2017 80

367-379

https://doi.org/10.1016/j.rser.2017.05.207

Dounis

A.I

Caraiscos

Advanced control systems engineering for energy and comfort management in a building environment-A review

Renewable and Sustainable Energy Reviews 2009 13 6-7

1246-1261

https://doi.org/10.1016/j.rser.2008.09.015

Z.J.

Control strategies for integration of thermal energy storage into buildings: State-of-the-art review

Energy and Buildings 2015 106

203-215

https://doi.org/10.1016/j.enbuild.2015.05.038

Perera

D.W.U.

Pfeiffer

>C.

Skeie

N.-O.

Control of temperature and energy consumption in buildings-A review

International Journal of Energy … Environment 2014 5 4

Thieblemont

Predictive control strategies based on weather forecast in buildings with energy storage system: A review of the state-of-the art

Energy and Buildings 2017 153

485-500

https://doi.org/10.1016/j.enbuild.2017.08.010

Shaikh

P.H.

A review on optimized control systems for building energy and comfort management of smart sustainable buildings

Renewable and Sustainable Energy Reviews 2014 34

409-429

https://doi.org/10.1016/j.rser.2014.03.027

Wang

Supervisory and optimal control of building HVAC systems: A review

Hvac…R Research 2008 14 1

3-32

https://doi.org/10.1080/10789669.2008.10390991

Afram

Janabi-Sharifi

Theory and applications of HVAC control systems-A review of model predictive control (MPC)

Building and Environment 2014 72

343-355

https://doi.org/10.1016/j.buildenv.2013.11.016

Mariano-Hernandez

A review of strategies for building energy management system: Model predictive control, demand side management, optimization, and fault detect … diagnosis

Journal of Building Engineering 2020

101692

https://doi.org/10.1016/j.jobe.2020.101692

Privara

Building modeling as a crucial part for building predictive control

Energy and Buildings 2013 56

8-22

https://doi.org/10.1016/j.enbuild.2012.10.024

Amasyali

El-Gohary

N.M.

A review of data-driven building energy consumption prediction studies

Renewable and Sustainable Energy Reviews 2018 81

1192-1205

https://doi.org/10.1016/j.rser.2017.04.095

Hazyuk

Ghiaus

Penhouet

Optimal temperature control of intermittently heated buildings using Model Predictive Control: Part I-Building modeling

Building and Environment 2012 51

379-387

https://doi.org/10.1016/j.buildenv.2011.11.009

Fan

A novel methodology to explain and evaluate data-driven building energy performance models based on interpretable machine learning

Applied Energy 2019 235

1551-1560

https://doi.org/10.1016/j.apenergy.2018.11.081

Krese

Determination of a Building's balance point temperature as an energy characteristic

Energy 2018 165

1034-1049

https://doi.org/10.1016/j.energy.2018.10.025

Macarulla

estimation of a room ventilation air change rate using a stochastic grey-box modelling approach

Measurement 2018 124

539-548

https://doi.org/10.1016/j.measurement.2018.04.029

Modeleon

The software dymola https://www.modelon.com/products/dymola/

TRNSYS

The software, transient system simulation too https://www.trnsys.com/

Zhao

EnergyPlus model-based predictive control within design-build-operate energy information modelling infrastructure

Journal of Building Performance Simulation 2015 8 3

121-134

https://doi.org/10.1080/19401493.2014.891656

Strachan

ESP-r: Summary of validation studies

Energy Systems Research Unit University of Strathclyde

Scotland, UK

2000

Afroz

Modeling techniques used in building HVAC control systems: A review

Renewable and Sustainable Energy Reviews 2018 83

64-84

https://doi.org/10.1016/j.rser.2017.10.044

Oldewurtel

use of model predictive control and weather forecasts for energy efficient building climate control

Energy and Buildings 2012 45

15-27

https://doi.org/10.1016/j.enbuild.2011.09.022

Drgon̂a

Explicit stochastic MPC approach to building temperature control

in 52nd IEEE Conference on Decision and Control 2013

IEEE

https://doi.org/10.1109/CDC.2013.6760908

Matuŝko

Borrelli

Stochastic model predictive control for building HVAC systems: Complexity and conservatism

IEEE Transactions on Control Systems Technology 2014 23 1

101-116

https://doi.org/10.1109/TCST.2014.2313736

Maasoumy

Handling model uncertainty in model predictive control for energy efficient buildings

Energy and Buildings 2014 77

377-392

https://doi.org/10.1016/j.enbuild.2014.03.057

Magni

Raimondo

D.M

Allgower

Nonlinear model predictive control

Lecture Notes in Control and Information Sciences 2009 384

https://doi.org/10.1007/978-3-642-01094-1

Camacho

E.F

Alba

C.B

Model predictive control 2013

Springer Science … Business Media

Mesbah

Stochastic model predictive control: An overview and perspectives for future research

IEEE Control Systems Magazine 2016 36 6

30-44

https://doi.org/10.1109/MCS.2016.2602087

Farina

Giulioni

Scattolini

Stochastic linear model predictive control with chance constraints-a review

Journal of Process Control 2016 44

53-67

https://doi.org/10.1016/j.jprocont.2016.03.005

Heirung

T.A.N.

Stochastic model predictive control-how does it work?

Computers … Chemical Engineering 2018 114

158-170

https://doi.org/10.1016/j.compchemeng.2017.10.026

Kall

Stochastic programming

European Journal of Operational Research 1982 10 2

125-130

https://doi.org/10.1016/0377-2217(82)90152-7

Birge

J.R

Louveaux

Introduction to stochastic programming 2011

Springer Science … Business Media

https://doi.org/10.1007/978-1-4614-0237-4

Lee

Y.I

Kouvaritakis

A linear programming approach to constrained robust predictive control

IEEE Transactions on Automatic Control 2000 45 9

1765-1770

https://doi.org/10.1109/9.880645

Grimm

Nominally robust model predictive control with state constraints

IEEE Transactions on Automatic Control 2007 52 10

1856-1870

https://doi.org/10.1109/TAC.2007.906187

Yan

Wang

Robust model predictive control of nonlinear systems with unmodeled dynamics and bounded uncertainties based on neural networks

IEEE transactions on neural networks and learning systems 2013 25 3

457-469

https://doi.org/10.1109/TNNLS.2013.2275948

Dong

Angeli

Tube-based robust Economic Model Predictive Control on dissipative systems with generalized optimal regimes of operation

in 2018 IEEE Conference on Decision and Control (CDC) 2018

IEEE

https://doi.org/10.1109/CDC.2018.8619325

Miller

B.L

Wagner

H.M

Chance constrained programming with joint constraints

Operations Research 1965 13 6

930-945

https://doi.org/10.1287/opre.13.6.930

Prekopa

On probabilistic constrained programming

in Proceedings of the Princeton symposium on mathematical programming 1970

Citeseer

Kall

Wallace

Kall

Stochastic programming 1994

Springer

Conejo

A.J.

Carrion

Morales

Decision making under uncertainty in electricity markets 1 2010

Springer

https://doi.org/10.1007/978-1-4419-7421-1_1

Heitsch

Romisch

A note on scenario reduction for two-stage stochastic programs

Operations Research Letters 2007 35 6

731-738

https://doi.org/10.1016/j.orl.2006.12.008

Dupacova

Growe-Kuska

Romisch

Scenario reduction in stochastic programming: An approach using probability metrics

2000 Humboldt-Universitat zu Berlin, Mathematisch-Naturwissenschaftliche Fakultät....

Frauendorfer

Barycentric scenario trees in convex multistage stochastic programming

Mathematical Programming 1996 75 2

277-293

https://doi.org/10.1007/BF02592156

Heitsch

Romisch

Scenario tree modeling for multistage stochastic programs

Mathematical Programming 2009 118 2

371-406

https://doi.org/10.1007/s10107-007-0197-2

Alqurashi

Etemadi

Khodaei

Model predictive control to two-stage stochastic dynamic economic dispatch problem

Control Engineering Practice 2017 69

112-121

https://doi.org/10.1016/j.conengprac.2017.09.012

Gabrel

Murat

Thiele

Recent advances in robust optimization: An overview

European journal of operational research 2014 235 3

471-483

https://doi.org/10.1016/j.ejor.2013.09.036

Bertsimas

Brown

Caramanis

Theory and applications of robust optimization

SIAM review 2011 53 3

464-501

https://doi.org/10.1137/080734510

Beyer

H.-G.

Sendhoff

Robust optimization-a comprehensive survey

Computer methods in applied mechanics and engineering 2007 196 33-34

3190-3218

https://doi.org/10.1016/j.cma.2007.03.003

Kothare

M.V.

Balakrishnan

Morari

Robust constrained model predictive control using linear matrix inequalities

Automatica 1996 32 10

1361-1379

https://doi.org/10.1016/0005-1098(96)00063-5

Perez-Lombard

Ortiz

Pout

A review on buildings energy consumption information

Energy and buildings 2008 40 3

394-398

https://doi.org/10.1016/j.enbuild.2007.03.007

Urge-Vorsatz

Energy use in buildings in a long-term perspective

Current Opinion in Environmental Sustainability 2013 5 2

141-151

https://doi.org/10.1016/j.cosust.2013.05.004

Deng

Wang

Dai

How to evaluate performance of net zero energy building-A literature research

Energy 2014 71

1-16

https://doi.org/10.1016/j.energy.2014.05.007

Torriti

Hassan

Leach

Demand response experience in Europe: Policies, programmes and implementation

Energy 2010 35 4

1575-1583

https://doi.org/10.1016/j.energy.2009.05.021

Ghahramani

Energy savings from temperature set-points and deadband: Quantifying the influence of building and system properties on savings

Applied Energy 2016 165

930-942

https://doi.org/10.1016/j.apenergy.2015.12.115

Kampelis

Evaluation of the performance gap in industrial, residential … tertiary near-Zero energy buildings

Energy and Buildings 2017 148

58-73

https://doi.org/10.1016/j.enbuild.2017.03.057

Hannan

M.A.

A review of internet of energy based building energy management systems: Issues and recommendations

Ieee Access 2018 6

38997-39014

https://doi.org/10.1109/ACCESS.2018.2852811

Han

Solanki

Coordinated predictive control of a wind/battery microgrid system

IEEE Journal of emerging and selected topics in power electronics 2013 1 4

296-305

https://doi.org/10.1109/JESTPE.2013.2282601

Bordons

Camacho

Model predictive control1 2007

Springer Verlag London Limited

Killian

Kozek

Ten questions concerning model predictive control for energy efficient buildings

Building and Environment 2016 105

403-412

https://doi.org/10.1016/j.buildenv.2016.05.034

Scattolini

Architectures for distributed and hierarchical model predictive control-a review

Journal of process control 2009 19 5

723-731

https://doi.org/10.1016/j.jprocont.2009.02.003

Negenborn

R.R

Maestre

Distributed model predictive control: An overview and roadmap of future research opportunities

IEEE Control Systems Magazine 2014 34 4

87-97

https://doi.org/10.1109/MCS.2014.2320397

Peeters

Compernolle

Van Passel

Simulation of a controlled water heating system with demand response remunerated on imbalance market pricing

Journal of Building Engineering 2020 27

100969

https://doi.org/10.1016/j.jobe.2019.100969

Perez

K.X.

Baldea

Edgar

Integrated HVAC management and optimal scheduling of smart appliances for community peak load reduction

Energy and Buildings 2016 123

34-40

https://doi.org/10.1016/j.enbuild.2016.04.003

Finck

Zeiler

Economic model predictive control for demand flexibility of a residential building

Energy 2019 176

365-379

https://doi.org/10.1016/j.energy.2019.03.171

Liu

Shi

Model predictive control for thermostatically controlled appliances providing balancing service

IEEE Transactions on Control Systems Technology 2016 24 6

2082-2093

https://doi.org/10.1109/TCST.2016.2535400

Mahdavi

Model predictive control of distributed air-conditioning loads to compensate fluctuations in solar power

IEEE Transactions on Smart Grid 2017 8 6

3055-3065

https://doi.org/10.1109/TSG.2017.2717447

Biyik

Kahraman

A predictive control strategy for optimal management of peak load, thermal comfort, energy storage and renewables in multi-zone buildings

Journal of building engineering 2019 25

100826

https://doi.org/10.1016/j.jobe.2019.100826

Bruno

Giannoccaro

La Scala

A Demand Response Implementation in Tertiary Buildings through Model Predictive Control

IEEE Transactions on Industry Applications 2019 55 6

7052-7061

https://doi.org/10.1109/TIA.2019.2932963

Halamay

D.A.

Starrett

Brekken

Hardware Testing of Electric Hot Water Heaters Providing Energy Storage and Demand Response Through Model Predictive Control

IEEE Access 2019 7

139047-139057

https://doi.org/10.1109/ACCESS.2019.2932978

Drgon̂a

Approximate model predictive building control via machine learning

Applied Energy 2018 218

199-216

https://doi.org/10.1016/j.apenergy.2018.02.156

Zhou

Cai

A dynamic water-filling method for real-time HVAC load control based on model predictive control

IEEE Transactions on Power Systems 2014 30 3

1405-1414

https://doi.org/10.1109/TPWRS.2014.2340881

Salakij

Model-Based Predictive Control for building energy management. I: Energy modeling and optimal control

Energy and Buildings 2016 133

345-358

https://doi.org/10.1016/j.enbuild.2016.09.044

Model-based predictive control for building energy management: Part II-Experimental validations

Energy and Buildings 2017 146

19-26

https://doi.org/10.1016/j.enbuild.2017.04.027

Schirrer

Nonlinear model predictive control for a heating and cooling system of a low-energy office building

Energy and Buildings 2016 125

86-98

https://doi.org/10.1016/j.enbuild.2016.04.029

Staino

Nagpal

Basu

Cooperative optimization of building energy systems in an economic model predictive control framework

Energy and Buildings 2016 128

713-722

https://doi.org/10.1016/j.enbuild.2016.07.009

Miyazaki

Design and value evaluation of demand response based on model predictive control

IEEE Transactions on Industrial Informatics 2019 15 8

4809-4818

https://doi.org/10.1109/TII.2019.2920373

Mbungu

N.T.

An optimal energy management system for a commercial building with renewable energy generation under real-time electricity prices

Sustainable cities and society 2018 41

392-404

https://doi.org/10.1016/j.scs.2018.05.049

Garifi

Stochastic model predictive control for demand response in a home energy management system

in 2018 IEEE Power … Energy Society General Meeting (PESGM) 2018

IEEE

https://doi.org/10.1109/PESGM.2018.8586485

Oldewurtel

Stochastic model predictive control for building climate control

IEEE Transactions on Control Systems Technology 2013 22 3

1198-1205

https://doi.org/10.1109/TCST.2013.2272178

Oldewurtel

Energy efficient building climate control using stochastic model predictive control and weather predictions

Proceedings of the 2010 American control conference 2010

IEEE

https://doi.org/10.1109/ACC.2010.5530680

Kumar

Stochastic model predictive control for central HVAC plants

Journal of Process Control 2020 90

1-17

https://doi.org/10.1016/j.jprocont.2020.03.015

Nasir

H.A.

Stochastic Model Predictive Control Based Reference Planning for Automated Open-Water Channels

IEEE Transactions on Control Systems Technology 2019

Arasteh

Riahy

MPC-based approach for online demand side and storage system management in market based wind integrated power systems

International Journal of Electrical Power … Energy Systems 2019 106

124-137

https://doi.org/10.1016/j.ijepes.2018.09.041

Razmara

Building-to-grid predictive power flow control for demand response and demand flexibility programs

Applied Energy 2017 203

128-141

https://doi.org/10.1016/j.apenergy.2017.06.040

Cao

Soleymanzadeh

Model predictive control of commercial buildings in demand response programs in the presence of thermal storage

Journal of Cleaner Production 2019 218

315-327

https://doi.org/10.1016/j.jclepro.2019.01.266

Bianchini

An integrated model predictive control approach for optimal HVAC and energy storage operation in large-scale buildings

Applied Energy 2019 240

327-340

https://doi.org/10.1016/j.apenergy.2019.01.187

Zong

Challenges of implementing economic model predictive control strategy for buildings interacting with smart energy systems

Applied Thermal Engineering 2017 114

1476-1486

https://doi.org/10.1016/j.applthermaleng.2016.11.141

Hovgaard

T.G.

Model predictive control technologies for efficient and flexible power consumption in refrigeration systems

Energy 2012 44 1

105-116

https://doi.org/10.1016/j.energy.2011.12.007

Ruusu

Direct quantification of multiple-source energy flexibility in a residential building using a new model predictive high-level controller

Energy Conversion and Management 2019 180

1109-1128

https://doi.org/10.1016/j.enconman.2018.11.026

Gomez-Romero

A probabilistic algorithm for predictive control with full-complexity models in non-residential buildings

IEEE Access 2019 7

38748-38765

https://doi.org/10.1109/ACCESS.2019.2906311

Megahed

T.F.

Abdelkader

Zakaria

Energy management in zero-energy building using neural network predictive control

IEEE Internet of Things Journal 2019 6 3

5336-5344

https://doi.org/10.1109/JIOT.2019.2900558

Cartagena

Munoz-Carpintero

Saez

A Robust Predictive Control Strategy for Building HVAC Systems Based on Interval Fuzzy Models

2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE) 2018

IEEE

https://doi.org/10.1109/FUZZ-IEEE.2018.8491442

Hosseini

S.M.

Carli

Dotoli

A Residential Demand-Side Management Strategy under Nonlinear Pricing Based on Robust Model Predictive Control

2019 IEEE International Conference on Systems, Man and Cybernetics (SMC) 2019

IEEE

https://doi.org/10.1109/SMC.2019.8913892

Model predictive control based robust scheduling of community integrated energy system with operational flexibility

Applied energy 2019 243

250-265

https://doi.org/10.1016/j.apenergy.2019.03.205

Nassourou

Blesa

Puig

Robust Economic Model Predictive Control Based on a Zonotope and Local Feedback Controller for Energy Dispatch in Smart-Grids Considering Demand Uncertainty

Energies 2020 13 3

696

https://doi.org/10.3390/en13030696

Nassourou

Puig

Blesa

Robust optimization based energy dispatch in smart grids considering simultaneously multiple uncertainties: Load demands and energy prices

IFAC-PapersOnLine 2017 50 1

6755-6760

https://doi.org/10.1016/j.ifacol.2017.08.1175

Yang

An adaptive robust model predictive control for indoor climate optimization and uncertainties handling in buildings

Building and Environment 2019 163

106326

https://doi.org/10.1016/j.buildenv.2019.106326

Tanaskovic

Robust adaptive model predictive building climate control

IFAC-PapersOnLine 2017 50 1

1871-1876

https://doi.org/10.1016/j.ifacol.2017.08.257

Antonov

Helsen

Robustness analysis of a hybrid ground coupled heat pump system with model predictive control

Journal of Process Control 2016 47

191-200

https://doi.org/10.1016/j.jprocont.2016.08.009

Shapiro

Monte Carlo sampling methods

Handbooks in operations research and management science 2003 10

353-425

https://doi.org/10.1016/S0927-0507(03)10006-0

Hedman

The application of robust optimization in power systems

Final Report to the Power Systems Engineering Research Center PSERC Publication 2014

14-6

Ben-Tal

El Ghaoui

Nemirovski

Robust optimization 28 2009

Princeton University Press

https://doi.org/10.1515/9781400831050

Mayne

Robust and stochastic model predictive control: Are we going in the right direction?

Annual Reviews in Control 2016 41

184-192

https://doi.org/10.1016/j.arcontrol.2016.04.006

REFERENCES

Kirschen D., Strbac G., Transmission networks and electricity markets, Fundamentals of power system economics, pp 141-204, 2004, https://doi.org/https://doi.org/10.1002/0470020598.ch6
Alam M., Arefifar S., Energy Management in power distribution systems: review, classification, limitations and challenges, IEEE Access, Vol. 7 , pp 92979-93001, 2019, https://doi.org/https://doi.org/10.1109/ACCESS.2019.2927303
Rafique S., Jianhua Z., Energy management system, generation and demand predictors: a review, IET Generation, Transmission … Distribution, Vol. 12 (3), pp 519-530, 2017, https://doi.org/https://doi.org/10.1049/iet-gtd.2017.0354
IEA, , Demand Response, 2020
Vardakas J., Zorba N., Verikoukis C., A survey on demand response programs in smart grids: Pricing methods and optimization algorithms, IEEE Communications Surveys … Tutorials, Vol. 17 (1), pp 152-178, 2014, https://doi.org/https://doi.org/10.1109/COMST.2014.2341586
Palensky P., Dietrich D., Demand side management: Demand response, intelligent energy systems, and smart loads, IEEE transactions on industrial informatics, Vol. 7 (3), pp 381-388, 2011, https://doi.org/https://doi.org/10.1109/TII.2011.2158841
Scheller F., Provoking residential demand response through variable electricity tariffs-a model-based assessment for municipal energy utilities, Technology and Economics of Smart Grids and Sustainable Energy, Vol. 3 (1), pp 7, 2018, https://doi.org/https://doi.org/10.1007/s40866-018-0045-x
Parrish B., Heptonstall P., Gross R., The potential for UK residential demand side participation, System Architecture Challenges: Supergen+ for HubNet, 2016
Uddin M., A review on peak load shaving strategies, Renewable and Sustainable Energy Reviews, Vol. 82 , pp 3323-3332, 2018, https://doi.org/https://doi.org/10.1016/j.rser.2017.10.056
Meyabadi A., Deihimi M., A review of demand-side management: Reconsidering theoretical framework, Renewable and Sustainable Energy Reviews, Vol. 80 , pp 367-379, 2017, https://doi.org/https://doi.org/10.1016/j.rser.2017.05.207
Dounis A., Caraiscos C., Advanced control systems engineering for energy and comfort management in a building environment-A review, Renewable and Sustainable Energy Reviews, Vol. 13 (6-7), pp 1246-1261, 2009, https://doi.org/https://doi.org/10.1016/j.rser.2008.09.015
Yu Z., Control strategies for integration of thermal energy storage into buildings: State-of-the-art review, Energy and Buildings, Vol. 106 , pp 203-215, 2015, https://doi.org/https://doi.org/10.1016/j.enbuild.2015.05.038
Perera D., Pfeiffer >., Skeie N., Control of temperature and energy consumption in buildings-A review, International Journal of Energy … Environment, Vol. 5 (4), 2014
Thieblemont H., Predictive control strategies based on weather forecast in buildings with energy storage system: A review of the state-of-the art, Energy and Buildings, Vol. 153 , pp 485-500, 2017, https://doi.org/https://doi.org/10.1016/j.enbuild.2017.08.010
Shaikh P., A review on optimized control systems for building energy and comfort management of smart sustainable buildings, Renewable and Sustainable Energy Reviews, Vol. 34 , pp 409-429, 2014, https://doi.org/https://doi.org/10.1016/j.rser.2014.03.027
Wang S., Ma Z., Supervisory and optimal control of building HVAC systems: A review, Hvac…R Research, Vol. 14 (1), pp 3-32, 2008, https://doi.org/https://doi.org/10.1080/10789669.2008.10390991
Afram A., Janabi-Sharifi F., Theory and applications of HVAC control systems-A review of model predictive control (MPC), Building and Environment, Vol. 72 , pp 343-355, 2014, https://doi.org/https://doi.org/10.1016/j.buildenv.2013.11.016
Mariano-Hernandez D., A review of strategies for building energy management system: Model predictive control, demand side management, optimization, and fault detect … diagnosis, Journal of Building Engineering, pp 101692, 2020, https://doi.org/https://doi.org/10.1016/j.jobe.2020.101692
Privara S., Building modeling as a crucial part for building predictive control, Energy and Buildings, Vol. 56 , pp 8-22, 2013, https://doi.org/https://doi.org/10.1016/j.enbuild.2012.10.024
Amasyali K., El-Gohary N., A review of data-driven building energy consumption prediction studies, Renewable and Sustainable Energy Reviews, Vol. 81 , pp 1192-1205, 2018, https://doi.org/https://doi.org/10.1016/j.rser.2017.04.095
Hazyuk I., Ghiaus C., Penhouet D., Optimal temperature control of intermittently heated buildings using Model Predictive Control: Part I-Building modeling, Building and Environment, Vol. 51 , pp 379-387, 2012, https://doi.org/https://doi.org/10.1016/j.buildenv.2011.11.009
Fan C., A novel methodology to explain and evaluate data-driven building energy performance models based on interpretable machine learning, Applied Energy, Vol. 235 , pp 1551-1560, 2019, https://doi.org/https://doi.org/10.1016/j.apenergy.2018.11.081
Krese G., Determination of a Building's balance point temperature as an energy characteristic, Energy, Vol. 165 , pp 1034-1049, 2018, https://doi.org/https://doi.org/10.1016/j.energy.2018.10.025
Macarulla M., estimation of a room ventilation air change rate using a stochastic grey-box modelling approach, Measurement, Vol. 124 , pp 539-548, 2018, https://doi.org/https://doi.org/10.1016/j.measurement.2018.04.029
Modeleon, , The software dymola
TRNSYS, , The software, transient system simulation too,
Zhao J., EnergyPlus model-based predictive control within design-build-operate energy information modelling infrastructure, Journal of Building Performance Simulation, Vol. 8 (3), pp 121-134, 2015, https://doi.org/https://doi.org/10.1080/19401493.2014.891656
Strachan P., ESP-r: Summary of validation studies, Energy Systems Research Unit, 2000
Afroz Z., Modeling techniques used in building HVAC control systems: A review, Renewable and Sustainable Energy Reviews, Vol. 83 , pp 64-84, 2018, https://doi.org/https://doi.org/10.1016/j.rser.2017.10.044
Oldewurtel F., use of model predictive control and weather forecasts for energy efficient building climate control, Energy and Buildings, Vol. 45 , pp 15-27, 2012, https://doi.org/https://doi.org/10.1016/j.enbuild.2011.09.022
Drgon̂a J., , in 52nd IEEE Conference on Decision and Control, 2013
Ma Y., Matuŝko J., Borrelli F., Stochastic model predictive control for building HVAC systems: Complexity and conservatism, IEEE Transactions on Control Systems Technology, Vol. 23 (1), pp 101-116, 2014, https://doi.org/https://doi.org/10.1109/TCST.2014.2313736
Maasoumy M., Handling model uncertainty in model predictive control for energy efficient buildings, Energy and Buildings, Vol. 77 , pp 377-392, 2014, https://doi.org/https://doi.org/10.1016/j.enbuild.2014.03.057
Magni L., Raimondo D., Allgower F., Nonlinear model predictive control, Lecture Notes in Control and Information Sciences, (384), 2009, https://doi.org/https://doi.org/10.1007/978-3-642-01094-1
Camacho E., Alba C., , Model predictive control, 2013
Mesbah A., Stochastic model predictive control: An overview and perspectives for future research, IEEE Control Systems Magazine, Vol. 36 (6), pp 30-44, 2016, https://doi.org/https://doi.org/10.1109/MCS.2016.2602087
Farina M., Giulioni L., Scattolini R., Stochastic linear model predictive control with chance constraints-a review, Journal of Process Control, Vol. 44 , pp 53-67, 2016, https://doi.org/https://doi.org/10.1016/j.jprocont.2016.03.005
Heirung T., Stochastic model predictive control-how does it work?, Computers … Chemical Engineering, Vol. 114 , pp 158-170, 2018, https://doi.org/https://doi.org/10.1016/j.compchemeng.2017.10.026
Kall P., Stochastic programming, European Journal of Operational Research, Vol. 10 (2), pp 125-130, 1982, https://doi.org/https://doi.org/10.1016/0377-2217(82)90152-7
Birge J., Louveaux F., , Introduction to stochastic programming, 2011
Lee Y., Kouvaritakis B., A linear programming approach to constrained robust predictive control, IEEE Transactions on Automatic Control, Vol. 45 (9), pp 1765-1770, 2000, https://doi.org/https://doi.org/10.1109/9.880645
Grimm G., Nominally robust model predictive control with state constraints, IEEE Transactions on Automatic Control, Vol. 52 (10), pp 1856-1870, 2007, https://doi.org/https://doi.org/10.1109/TAC.2007.906187
Yan Z., Wang J., Robust model predictive control of nonlinear systems with unmodeled dynamics and bounded uncertainties based on neural networks, IEEE transactions on neural networks and learning systems, Vol. 25 (3), pp 457-469, 2013, https://doi.org/https://doi.org/10.1109/TNNLS.2013.2275948
Dong Z., Angeli D., , in 2018 IEEE Conference on Decision and Control (CDC), 2018
Miller B., Wagner H., Chance constrained programming with joint constraints, Operations Research, Vol. 13 (6), pp 930-945, 1965, https://doi.org/https://doi.org/10.1287/opre.13.6.930
Prekopa A., , in Proceedings of the Princeton symposium on mathematical programming, 1970
Kall P., Wallace S., Kall P., , Stochastic programming, 1994
Conejo A., Carrion M., Morales J., , Decision making under uncertainty in electricity markets, 2010
Heitsch H., Romisch W., A note on scenario reduction for two-stage stochastic programs, Operations Research Letters, Vol. 35 (6), pp 731-738, 2007, https://doi.org/https://doi.org/10.1016/j.orl.2006.12.008
Dupacova J., Growe-Kuska N., Romisch W., Scenario reduction in stochastic programming: An approach using probability metrics, Humboldt-Universitat zu Berlin, Mathematisch-Naturwissenschaftliche Fakultät...., 2000
Frauendorfer K., Barycentric scenario trees in convex multistage stochastic programming, Mathematical Programming, Vol. 75 (2), pp 277-293, 1996, https://doi.org/https://doi.org/10.1007/BF02592156
Heitsch H., Romisch W., Scenario tree modeling for multistage stochastic programs, Mathematical Programming, Vol. 118 (2), pp 371-406, 2009, https://doi.org/https://doi.org/10.1007/s10107-007-0197-2
Alqurashi A., Etemadi A., Khodaei A., Model predictive control to two-stage stochastic dynamic economic dispatch problem, Control Engineering Practice, Vol. 69 , pp 112-121, 2017, https://doi.org/https://doi.org/10.1016/j.conengprac.2017.09.012
Gabrel V., Murat C., Thiele A., Recent advances in robust optimization: An overview, European journal of operational research, Vol. 235 (3), pp 471-483, 2014, https://doi.org/https://doi.org/10.1016/j.ejor.2013.09.036
Bertsimas D., Brown D., Caramanis C., Theory and applications of robust optimization, SIAM review, Vol. 53 (3), pp 464-501, 2011, https://doi.org/https://doi.org/10.1137/080734510
Beyer H., Sendhoff B., Robust optimization-a comprehensive survey, Computer methods in applied mechanics and engineering, Vol. 196 (33-34), pp 3190-3218, 2007, https://doi.org/https://doi.org/10.1016/j.cma.2007.03.003
Kothare M., Balakrishnan V., Morari M., Robust constrained model predictive control using linear matrix inequalities, Automatica, Vol. 32 (10), pp 1361-1379, 1996, https://doi.org/https://doi.org/10.1016/0005-1098(96)00063-5
Lombard L., Ortiz J., Pout C., A review on buildings energy consumption information, Energy and buildings, Vol. 40 (3), pp 394-398, 2008, https://doi.org/https://doi.org/10.1016/j.enbuild.2007.03.007
Urge-Vorsatz D., Energy use in buildings in a long-term perspective, Current Opinion in Environmental Sustainability, Vol. 5 (2), pp 141-151, 2013, https://doi.org/https://doi.org/10.1016/j.cosust.2013.05.004
Deng S., Wang R., Dai Y., How to evaluate performance of net zero energy building-A literature research, Energy, Vol. 71 , pp 1-16, 2014, https://doi.org/https://doi.org/10.1016/j.energy.2014.05.007
Torriti J., Hassan M., Leach M., Demand response experience in Europe: Policies, programmes and implementation, Energy, Vol. 35 (4), pp 1575-1583, 2010, https://doi.org/https://doi.org/10.1016/j.energy.2009.05.021
Ghahramani A., Energy savings from temperature set-points and deadband: Quantifying the influence of building and system properties on savings, Applied Energy, Vol. 165 , pp 930-942, 2016, https://doi.org/https://doi.org/10.1016/j.apenergy.2015.12.115
Kampelis N., Evaluation of the performance gap in industrial, residential … tertiary near-Zero energy buildings, Energy and Buildings, Vol. 148 , pp 58-73, 2017, https://doi.org/https://doi.org/10.1016/j.enbuild.2017.03.057
Hannan M., A review of internet of energy based building energy management systems: Issues and recommendations, Ieee Access, Vol. 6 , pp 38997-39014, 2018, https://doi.org/https://doi.org/10.1109/ACCESS.2018.2852811
Han J., Solanki S., Solanki J., Coordinated predictive control of a wind/battery microgrid system, IEEE Journal of emerging and selected topics in power electronics, Vol. 1 (4), pp 296-305, 2013, https://doi.org/https://doi.org/10.1109/JESTPE.2013.2282601
Bordons C., Camacho E., , Model predictive control1, 2007
Killian M., Kozek M., Ten questions concerning model predictive control for energy efficient buildings, Building and Environment, Vol. 105 , pp 403-412, 2016, https://doi.org/https://doi.org/10.1016/j.buildenv.2016.05.034
Scattolini R., Architectures for distributed and hierarchical model predictive control-a review, Journal of process control, Vol. 19 (5), pp 723-731, 2009, https://doi.org/https://doi.org/10.1016/j.jprocont.2009.02.003
Negenborn R., Maestre J., Distributed model predictive control: An overview and roadmap of future research opportunities, IEEE Control Systems Magazine, Vol. 34 (4), pp 87-97, 2014, https://doi.org/https://doi.org/10.1109/MCS.2014.2320397
Peeters M., Compernolle T., Van Passel S., Simulation of a controlled water heating system with demand response remunerated on imbalance market pricing, Journal of Building Engineering, Vol. 27 , pp 100969, 2020, https://doi.org/https://doi.org/10.1016/j.jobe.2019.100969
Perez K., Baldea M., Edgar T., Integrated HVAC management and optimal scheduling of smart appliances for community peak load reduction, Energy and Buildings, Vol. 123 , pp 34-40, 2016, https://doi.org/https://doi.org/10.1016/j.enbuild.2016.04.003
Finck C., Li R., Zeiler W., Economic model predictive control for demand flexibility of a residential building, Energy, Vol. 176 , pp 365-379, 2019, https://doi.org/https://doi.org/10.1016/j.energy.2019.03.171
Liu M., Shi Y., Model predictive control for thermostatically controlled appliances providing balancing service, IEEE Transactions on Control Systems Technology, Vol. 24 (6), pp 2082-2093, 2016, https://doi.org/https://doi.org/10.1109/TCST.2016.2535400
Mahdavi N., Model predictive control of distributed air-conditioning loads to compensate fluctuations in solar power, IEEE Transactions on Smart Grid, Vol. 8 (6), pp 3055-3065, 2017, https://doi.org/https://doi.org/10.1109/TSG.2017.2717447
Biyik E., Kahraman A., A predictive control strategy for optimal management of peak load, thermal comfort, energy storage and renewables in multi-zone buildings, Journal of building engineering, Vol. 25 , pp 100826, 2019, https://doi.org/https://doi.org/10.1016/j.jobe.2019.100826
Bruno S., Giannoccaro G., La Scala M., A Demand Response Implementation in Tertiary Buildings through Model Predictive Control, IEEE Transactions on Industry Applications, Vol. 55 (6), pp 7052-7061, 2019, https://doi.org/https://doi.org/10.1109/TIA.2019.2932963
Halamay D., Starrett M., Brekken T., Hardware Testing of Electric Hot Water Heaters Providing Energy Storage and Demand Response Through Model Predictive Control, IEEE Access, Vol. 7 , pp 139047-139057, 2019, https://doi.org/https://doi.org/10.1109/ACCESS.2019.2932978
Drgon̂a J., Approximate model predictive building control via machine learning, Applied Energy, Vol. 218 , pp 199-216, 2018, https://doi.org/https://doi.org/10.1016/j.apenergy.2018.02.156
Zhou K., Cai L., A dynamic water-filling method for real-time HVAC load control based on model predictive control, IEEE Transactions on Power Systems, Vol. 30 (3), pp 1405-1414, 2014, https://doi.org/https://doi.org/10.1109/TPWRS.2014.2340881
Salakij S., Model-Based Predictive Control for building energy management. I: Energy modeling and optimal control, Energy and Buildings, Vol. 133 , pp 345-358, 2016, https://doi.org/https://doi.org/10.1016/j.enbuild.2016.09.044
Yu N., Model-based predictive control for building energy management: Part II-Experimental validations, Energy and Buildings, Vol. 146 , pp 19-26, 2017, https://doi.org/https://doi.org/10.1016/j.enbuild.2017.04.027
Schirrer A., Nonlinear model predictive control for a heating and cooling system of a low-energy office building, Energy and Buildings, Vol. 125 , pp 86-98, 2016, https://doi.org/https://doi.org/10.1016/j.enbuild.2016.04.029
Staino A., Nagpal H., Basu B., Cooperative optimization of building energy systems in an economic model predictive control framework, Energy and Buildings, Vol. 128 , pp 713-722, 2016, https://doi.org/https://doi.org/10.1016/j.enbuild.2016.07.009
Miyazaki K., Design and value evaluation of demand response based on model predictive control, IEEE Transactions on Industrial Informatics, Vol. 15 (8), pp 4809-4818, 2019, https://doi.org/https://doi.org/10.1109/TII.2019.2920373
Mbungu N., An optimal energy management system for a commercial building with renewable energy generation under real-time electricity prices, Sustainable cities and society, Vol. 41 , pp 392-404, 2018, https://doi.org/https://doi.org/10.1016/j.scs.2018.05.049
Garifi K., , in 2018 IEEE Power … Energy Society General Meeting (PESGM), 2018
Oldewurtel F., Stochastic model predictive control for building climate control, IEEE Transactions on Control Systems Technology, Vol. 22 (3), pp 1198-1205, 2013, https://doi.org/https://doi.org/10.1109/TCST.2013.2272178
Oldewurtel F., , Proceedings of the 2010 American control conference, 2010
Kumar R., Stochastic model predictive control for central HVAC plants, Journal of Process Control, Vol. 90 , pp 1-17, 2020, https://doi.org/https://doi.org/10.1016/j.jprocont.2020.03.015
Nasir H., Stochastic Model Predictive Control Based Reference Planning for Automated Open-Water Channels, IEEE Transactions on Control Systems Technology, 2019
Arasteh F., Riahy G., MPC-based approach for online demand side and storage system management in market based wind integrated power systems, International Journal of Electrical Power … Energy Systems, Vol. 106 , pp 124-137, 2019, https://doi.org/https://doi.org/10.1016/j.ijepes.2018.09.041
Razmara M., Building-to-grid predictive power flow control for demand response and demand flexibility programs, Applied Energy, Vol. 203 , pp 128-141, 2017, https://doi.org/https://doi.org/10.1016/j.apenergy.2017.06.040
Cao Y., Du J., Soleymanzadeh E., Model predictive control of commercial buildings in demand response programs in the presence of thermal storage, Journal of Cleaner Production, Vol. 218 , pp 315-327, 2019, https://doi.org/https://doi.org/10.1016/j.jclepro.2019.01.266
Bianchini G., An integrated model predictive control approach for optimal HVAC and energy storage operation in large-scale buildings, Applied Energy, Vol. 240 , pp 327-340, 2019, https://doi.org/https://doi.org/10.1016/j.apenergy.2019.01.187
Zong Y., Challenges of implementing economic model predictive control strategy for buildings interacting with smart energy systems, Applied Thermal Engineering, Vol. 114 , pp 1476-1486, 2017, https://doi.org/https://doi.org/10.1016/j.applthermaleng.2016.11.141
Hovgaard T., Model predictive control technologies for efficient and flexible power consumption in refrigeration systems, Energy, Vol. 44 (1), pp 105-116, 2012, https://doi.org/https://doi.org/10.1016/j.energy.2011.12.007
Ruusu R., Direct quantification of multiple-source energy flexibility in a residential building using a new model predictive high-level controller, Energy Conversion and Management, Vol. 180 , pp 1109-1128, 2019, https://doi.org/https://doi.org/10.1016/j.enconman.2018.11.026
Gomez-Romero J., A probabilistic algorithm for predictive control with full-complexity models in non-residential buildings, IEEE Access, Vol. 7 , pp 38748-38765, 2019, https://doi.org/https://doi.org/10.1109/ACCESS.2019.2906311
Megahed T., Abdelkader S., Zakaria A., Energy management in zero-energy building using neural network predictive control, IEEE Internet of Things Journal, Vol. 6 (3), pp 5336-5344, 2019, https://doi.org/https://doi.org/10.1109/JIOT.2019.2900558
Cartagena O., Munoz-Carpintero D., Saez D., , 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), 2018
Hosseini S., Carli R., Dotoli M., A Residential Demand-Side Management Strategy under Nonlinear Pricing Based on Robust Model Predictive Control, 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), 2019, https://doi.org/https://doi.org/10.1109/SMC.2019.8913892
Lv C., Model predictive control based robust scheduling of community integrated energy system with operational flexibility, Applied energy, Vol. 243 , pp 250-265, 2019, https://doi.org/https://doi.org/10.1016/j.apenergy.2019.03.205
Nassourou M., Blesa J., Puig V., Robust Economic Model Predictive Control Based on a Zonotope and Local Feedback Controller for Energy Dispatch in Smart-Grids Considering Demand Uncertainty, Energies, Vol. 13 (3), pp 696, 2020, https://doi.org/https://doi.org/10.3390/en13030696
Nassourou M., Puig V., Blesa J., Robust optimization based energy dispatch in smart grids considering simultaneously multiple uncertainties: Load demands and energy prices, IFAC-PapersOnLine, Vol. 50 (1), pp 6755-6760, 2017, https://doi.org/https://doi.org/10.1016/j.ifacol.2017.08.1175
Yang S., An adaptive robust model predictive control for indoor climate optimization and uncertainties handling in buildings, Building and Environment, Vol. 163 , pp 106326, 2019, https://doi.org/https://doi.org/10.1016/j.buildenv.2019.106326
Tanaskovic M., Robust adaptive model predictive building climate control, IFAC-PapersOnLine, Vol. 50 (1), pp 1871-1876, 2017, https://doi.org/https://doi.org/10.1016/j.ifacol.2017.08.257
Antonov S., Helsen L., Robustness analysis of a hybrid ground coupled heat pump system with model predictive control, Journal of Process Control, Vol. 47 , pp 191-200, 2016, https://doi.org/https://doi.org/10.1016/j.jprocont.2016.08.009
Shapiro A., Monte Carlo sampling methods, Handbooks in operations research and management science, Vol. 10 , pp 353-425, 2003, https://doi.org/https://doi.org/10.1016/S0927-0507(03)10006-0
Hedman K., The application of robust optimization in power systems, Final Report to the Power Systems Engineering Research Center, pp 14-6, 2014
Ben-Tal A., El Ghaoui L., Nemirovski A., , Robust optimization, 2009
Mayne D., Robust and stochastic model predictive control: Are we going in the right direction?, Annual Reviews in Control, Vol. 41 , pp 184-192, 2016, https://doi.org/https://doi.org/10.1016/j.arcontrol.2016.04.006